 |
|
Переместительное свойство
Можно ли в сходящемся ряде произвольно переставлять члены ряда? Этого делать нельзя. Рассмотрим пример такого ряда.
. (3)
Этот ряд знакочередующийся, он удовлетворяет всем условиям теоремы Лейбница. Ряд сходится, его сумма, как мы покажем далее, равна 
. Переместим члены ряда (3) так, чтобы после одного положительного шли два отрицательных:
. (4)
Покажем, что сумма ряда (4) вдвое меньше суммы ряда (3). Пусть 
и 
– частные суммы соответственно рядов (3) и (4). Тогда
.
Таким образом, 
при 
. Остаётся показать, что последовательности 
, 
имеют тот же предел. Это следует из равенств
, 
.
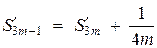Более того верна следующая
Теорема (Римана). Если дан действительный условно сходящийся ряд, то, каково бы ни было число, можно так переставить члены ряда, что вновь полученный ряд будет сходиться к этому числу. Также можно так переставить члены данного ряда, что вновь полученный ряд будет расходящимся.
Выделим теперь класс рядов, для которых переместительное свойство верно.
Теорема 2.Пусть дан произвольный абсолютно сходящийся ряд
(5)
с комплексными числами. Произвольная перестановка членов ряда не нарушает его абсолютной сходимости и не изменяет суммы.
Доказательство разобьём на несколько этапов
1) Докажем сначала теорему для положительного ряда
. (6)
Пусть 
– частная сумма и 
– сумма ряда (6). Переставим произвольно члены ряда (6), получим ряд
. (7)
Частные суммы ряда (7) обозначим через 
. Рассмотрим произвольную частную сумму .
Далее, если взять частную сумму ряда (6) с достаточно большим номером 
, то будут верны неравенства:
, 
.
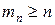Перейдём в первом неравенстве к пределу при 
. Получим, что для всех n
.
Видим, что частные суммы положительного ряда (7) ограничены сверху, поэтому ряд сходится. Пусть B – его сумма. Перейдём в последнем неравенстве к пределу при 
, получим
. (8)
Мы рассматривали ряд (7) как полученный из ряда (6) перестановкой членов ряда. Если же в рассуждениях поменять ролями ряды (6) и (7), то получим, что
. (9)
Из неравенств (8) и (9) следует равенство 
.
2) Докажем теперь теорему для произвольного абсолютно сходящегося ряда с действительными числами
. (10)
Составим ряд из всех положительных членов ряда (10)
(11)
и ряд из абсолютных величин всех отрицательных членов ряда (10)
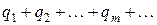. (12)
В рядах (11) и (12) члены их располагаются в том порядке, в каком они следовали в ряде (10). Покажем, что ряды (11) и (12) сходятся, причём, есл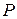и , 
и 
суммы соответственно рядов (10), (11) и (12), то верно равенство
. (13)
Пусть 
и 
– частные суммы и сумма ряда
. (14)
Обозначим через , 
и 
частные суммы соответственно рядов (10), (11) и (12), причём 
. Тогда легко видеть, что
, 
.
Частные суммы положительных рядов (11) и (12) ограничены сверху, значит, они сходятся. Далее, очевидно, что
= 
.
Переходя здесь к пределу при , получим равенство (13).
Заметим, что на абсолютно сходящийся ряд с действительными числами можно смотреть как на разность двух положительных рядов.
Теперь закончим доказательство этого пункта.
Перестановка членов ряда (10) ведёт к перестановке членов положительного ряда (14). Как следует из первого пункта теоремы, сходимость его не нарушается. Это значит, что ряд (10) и после перестановки сохраняет абсолютную сходимость.
Далее, эта же перестановка приводит к некоторой перестановке в положительных рядах (11) и (12), которая по первому пункту теоремы не нарушает сходимости рядов и их сумм. Но тогда и после перестановки сохраняется равенство
.
3) Теперь докажем теорему в общем случае
Итак, дан абсолютно сходящийся ряд с комплексными членами
(5)
Пусть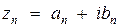 
. Рассмотрим ряды
, (15)
. (16)
Как известно ряды (15) и (16) сходятся, причём, если A и B соответственно их суммы, то верно равенство
. (17)
Но ряды (15) и (16) сходятся абсолютно, что следует из очевидных неравенств
, 
, 
и признака сравнения положительных рядов.
Произведём теперь перестановку членов ряда (5). Это приведёт к такой же перестановке в рядах (15) и (16), что по пункту 2 теоремы не на-рушает их абсолютной сходимости и не изменяет их суммы. А тогда в ре-зультате перестановки сохраняются сходимость ряда (5) и равенство (17).
Сходимость будет абсолютная, так как 
.
Умножение рядов
Пусть даны два ряда с комплексными членами
, (1)
. (2)
Рассмотрим всевозможные парные произведения членов этих рядов. Их можно расположить в виде матрицы
(3)
Все парные произведения можно многими способами расположить в виде последовательности, не пропустив ни одного. Например, их можно выписать по диагоналям матрицы:
,
или квадратам матрицы:
.
Теорема.Еслиряды (1) и (2) сходятся абсолютно, то ряд, составленный из всех парных произведений (3) и взятых в любом порядке, также сходится абсолютно, причём его сумма равна произведению сумм рядов (1) и (2).
Доказательство. Рассмотрим ряд из парных произведений, взятых в любом порядке
.
Для доказательства абсолютной сходимости этого ряда достаточно доказать абсолютную сходимость такого же ряда из парных произведений, взятых в каком-либо одном порядке, так как перестановки не нарушают абсолютной сходимости и его сумме.
По условию ряды
, (4)
, (5)
сходятся. Пусть их суммы равны 
и 
, частные суммы обозначим через 
и 
.
Рассмотрим ряд
(6)
Члены этого ряда образованы группировкой членов ряда
, (7)
в котором парные произведения рядов (4) и (5) расположены в соответствии с квадратами матрицы (3). Группировка сделана также в соответствии с этими квадратами. Нам надо доказать сходимость ряда (7).
Заметим, что частные суммы ряда (6) имеют вид 
, 
, ... , 
, … . Но тогда ряд (6) сходится к 
, так как
при 
.
Теперь опустим скобки в положительном ряде (6) и получим положительный ряд (7). Легко заметить, что любая частная сумма ряда (7)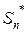 
находится между частными суммами ряда (6) с соседними номерами
Отсюда видим, что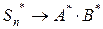 
, то есть ряд (6) сходится к 
.
Повторяя буквально все рассуждения для рядов (1) и (2), проведенные для рядов (4) и (5), мы найдём, что ряд
сходится к сумме 
, где и 
суммы рядов (1) и (2). Теперь можно опустить скобки в этом ряде, так как получаем сходящийся ряд.
Определение 1. Пусть даны ряды (1) и (2). Рядом-произведением рядов (1) и (2) назовём ряд
.
Члены этого ряда образованы из групп парных произведений матрицы (3), расположенных по её диагоналям. Это определение ряда-произведения по Коши.
Из доказанной теоремы вытекает, что если ряды (1) и (2) сходятся абсолютно, то ряд-произведение так же сходится абсолютно, причём сумма его будет произведением сумм рядов-сомножителей.
Замечание. Если ряды (1) и (2) не являются абсолютно сходящимися, а только сходящимися, то ряд-произведение их может расходиться.
Рассмотрим ряд 
.
Это условно сходящийся ряд. Умножим его на себя по правилу Коши, получим
.
Заметим, что 
. Тогда выражение в скобках будет больше единицы. Общий член ряда не стремится к нулю, ряд-произведение расходится.
Однако можно доказать, что если один ряд сходится абсолютно, а второй просто сходится, то ряд-произведение сходится к сумме, равной произведению сумм рядов-сомножителей.