 |
|
Список використаної літератури.
Ряди
Числові ряди
1.1. Теоретичні відомості та зразки розв’язання задач
Числовим рядом називається вираз

| (1) |
Числа  – члени числового ряду, un – загальний член ряду.
– члени числового ряду, un – загальний член ряду.
Сума n перших членів ряду  називається
називається  -ю частинною сумою ряду.
-ю частинною сумою ряду.
Якщо існує скінченна границя

| (2) |
то числовий ряд (1) називається збіжним, а число 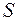 називається сумою ряду (1). Якщо границя (2) не існує, то ряд (1) називається розбіжним. Такий ряд суми не має.
називається сумою ряду (1). Якщо границя (2) не існує, то ряд (1) називається розбіжним. Такий ряд суми не має.
Різницю між сумою ряду  та його
та його  -ю частинною сумою
-ю частинною сумою  називають
називають  - м залишком збіжного ряду (1). Залишок ряду позначається через
- м залишком збіжного ряду (1). Залишок ряду позначається через  :
:

| (3) |
Суму 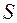 збіжного ряду (1) можна представити у вигляді:
збіжного ряду (1) можна представити у вигляді:
 .
.
Приклад 1. Скориставшись означенням суми числового ряду, обчислити суму ряду

Розв’язання. Послідовно знаходимо частинні суми ряду:

Запишемо послідовність частинних сум:  Загальний член цієї послідовності
Загальний член цієї послідовності  . За означенням, сума ряду
. За означенням, сума ряду  .
.
Отже, послідовність частинних сум має границю, яка дорівнює  . Таким чином, заданий ряд збігається і його сума
. Таким чином, заданий ряд збігається і його сума  .
.
Властивості числових рядів:
| 1) | Якщо ряд  збіжний і його сума дорівнює збіжний і його сума дорівнює 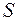 , то ряд , то ряд  також збіжний і його сума дорівнює також збіжний і його сума дорівнює  . Якщо ж ряд . Якщо ж ряд  розбігається і розбігається і  , то ряд , то ряд  також розбігається. також розбігається.
|
| 2) | Якщо числові ряди  та та 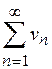 збіжні і збіжні і 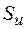 та та 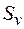 – їхні суми відповідно, то збіжні також ряди – їхні суми відповідно, то збіжні також ряди  і їхні суми дорівнюють і їхні суми дорівнюють 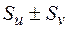 відповідно. відповідно.
|
Необхідна умова збіжності ряду.
Якщо ряд  збіжний, то збіжний, то  . .
|
Достатня умова розбіжності ряду.
Якщо 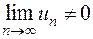 , то ряд
, то ряд  розбіжний.
розбіжний.
Приклад 2. Дослідити на збіжність числовий ряд

Розв’язання. Обчислимо границю
 .
.
Необхідна умова збіжності не виконується, заданий ряд розбіжний.

| Зауваження. Якщо необхідна умова виконується, то висновок про збіжність або розбіжність ряду тільки на основі цього факту зробити не можна. |
Приклад 3. Перевірити, чи виконується необхідна умова збіжності числового
ряду 
Розв’язання. Обчислимо границю
 .
.
Тут виконується необхідна умова збіжності числового ряду, проте вона не є достатньою для того, щоб зробити висновок про збіжність або розбіжність досліджуваного ряду.
Існують достатні ознаки збіжності, які дають можливість з’ясувати питання про поведінку ряду.
Ознака Даламбера.
Якщо для ряду з додатними членами  існує границя
існує границя  , то: 1) при , то: 1) при  ряд збіжний,
2) при ряд збіжний,
2) при  ряд розбіжний. ряд розбіжний.
|
При  слід застосовувати іншу ознаку.
слід застосовувати іншу ознаку.

| Зауваження. Ознаку Даламбера доцільно застосовувати до рядів, загальні члени яких містять показникові множники або факторіали. |
Приклад 4. Дослідити на збіжність ряд
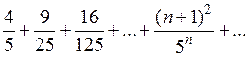
Розв’язання. Застосуємо ознаку Даламбера.
За умовою маємо  ,
,  .
.
Обчислимо 
 . За ознакою Даламбера даний ряд збіжний.
. За ознакою Даламбера даний ряд збіжний.
Приклад 5. Дослідити на збіжність ряд

Розв’язання. Запишемо  –й та
–й та  –й члени заданого ряду
–й члени заданого ряду
 ,
,  .
.

|
Зауваження.  ( в математиці « ( в математиці «  » – знак факторіалу). » – знак факторіалу).
|
 .
.

 – за ознакою Даламбера даний ряд збіжний.
– за ознакою Даламбера даний ряд збіжний.
Приклад 6. Дослідити на збіжність ряд
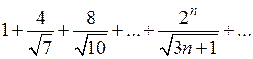
Розв’язання. Оскільки для заданого ряду
 ,
, 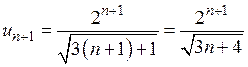 , то
, то

Отже,  – за ознакою Даламбера даний ряд розбіжний.
– за ознакою Даламбера даний ряд розбіжний.
Ознака порівняння рядів (гранична).
Нехай  і і  – знакододатні ряди – знакододатні ряди  , ,  .
Якщо існує скінченна, відмінна від нуля границя .
Якщо існує скінченна, відмінна від нуля границя 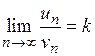 , ,  , ,  , то поведінка рядів однакова: якщо один з рядів збіжний (розбіжний), то і другий ряд також збіжний (розбіжний). , то поведінка рядів однакова: якщо один з рядів збіжний (розбіжний), то і другий ряд також збіжний (розбіжний).
|

| Зауваження. Для застосування цієї ознаки заданий ряд слушно порівнювати з рядом, збіжність (чи розбіжність) якого відома заздалегідь. |
Зокрема, це такі ряди:
· геометричний ряд (сума членів нескінченної геометричної прогресії)
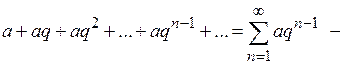 
| (4) |
· гармонічний ряд
 розбіжний; розбіжний;
| (5) |
· узагальнений гармонічний ряд
 
| (6) |
Приклад 7. Дослідити на збіжність ряд
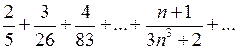
Розв’язання. Застосуємо ознаку порівняння рядів. Запишемо загальний член заданого ряду 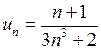 . Для порівняння оберемо ряд із загальним членом
. Для порівняння оберемо ряд із загальним членом  (який отримали, залишивши в чисельнику і знаменнику виразу для
(який отримали, залишивши в чисельнику і знаменнику виразу для  тільки старші степені змінної
тільки старші степені змінної  :
: 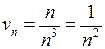 ). Ряд
). Ряд  – збіжний узагальнений гармонічний ряд, оскільки
– збіжний узагальнений гармонічний ряд, оскільки  . Маємо
. Маємо
 .
.
Оскільки границя  скінченна і
скінченна і  , то ряди ведуть себе однаково, тобто заданий ряд збіжний, як і ряд, обраний для порівняння.
, то ряди ведуть себе однаково, тобто заданий ряд збіжний, як і ряд, обраний для порівняння.
Приклад 8. Дослідити на збіжність ряд  .
.
Розв’язання. Запишемо загальний член заданого ряду  . Для порівняння оберемо ряд із загальним членом
. Для порівняння оберемо ряд із загальним членом 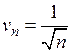
 .
.
Ряд  – розбіжний узагальнений гармонічний ряд, оскільки
– розбіжний узагальнений гармонічний ряд, оскільки  . Обчислимо
. Обчислимо 
 .
.
Оскільки границя  скінченна і
скінченна і  , то ряди ведуть себе однаково, тобто заданий ряд розбіжний, як і ряд, обраний для порівняння.
, то ряди ведуть себе однаково, тобто заданий ряд розбіжний, як і ряд, обраний для порівняння.
Знакозмінним називається ряд  , серед членів якого є як додатні, так і від’ємні (нескінченна кількість кожних).
, серед членів якого є як додатні, так і від’ємні (нескінченна кількість кожних).
Ряд вигляду
 , ,  , ,
| (7) |
знаки членів якого строго чергуються, називається знакопочережним.
Ознака Лейбніца.
Знакопочережний ряд (7) є збіжним, якщо:
1) члени його спадають за абсолютною величиною  , починаючи з деякого , починаючи з деякого  ( (  );
2) );
2)  . .
|
При цьому сума S ряду додатна і не перевищує першого його члена, 

| Зауваження. Перша умова ознаки Лейбніца може виконуватися не з початкових членів ряду, а починаючи з деякого, більш далекого. |

|
Зауваження. Якщо при обчисленні суми  збіжного знакопочережного ряду (7) врахувати тільки збіжного знакопочережного ряду (7) врахувати тільки  перших членів, то похибка наближення перших членів, то похибка наближення  за абсолютною величиною не перевищує абсолютної величини першого з відкинутих членів, тобто за абсолютною величиною не перевищує абсолютної величини першого з відкинутих членів, тобто  , або , або  , де , де  – –  й залишок збіжного ряду (7). й залишок збіжного ряду (7).
|
Знакозмінний ряд  збігається, якщо збігається ряд
збігається, якщо збігається ряд  , утворений з абсолютних величин його членів. В цьому випадку кажуть, що знакозмінний ряд
, утворений з абсолютних величин його членів. В цьому випадку кажуть, що знакозмінний ряд  збігається абсолютно.
збігається абсолютно.
Якщо знакозмінний ряд  збігається, а ряд
збігається, а ряд  розбігається, то знакозмінний ряд
розбігається, то знакозмінний ряд  називається умовно збіжним.
називається умовно збіжним.
Приклад 9. Дослідити на збіжність знакопочережний ряд

Розв’язання. Спочатку розглянемо ряд  , складений з абсолютних величин членів заданого ряду, і дослідимо його на збіжність.
, складений з абсолютних величин членів заданого ряду, і дослідимо його на збіжність.  – загальний член цього ряду. Для порівняння оберемо узагальнений гармонічний ряд
– загальний член цього ряду. Для порівняння оберемо узагальнений гармонічний ряд  , який є збіжним, оскільки
, який є збіжним, оскільки  . Його загальний член
. Його загальний член  . Маємо
. Маємо 
 – границя існує і
– границя існує і  . Це означає, що поведінка порівнюваних рядів однакова: оскільки ряд
. Це означає, що поведінка порівнюваних рядів однакова: оскільки ряд  збіжний, то збіжним є і ряд
збіжний, то збіжним є і ряд  , складений з абсолютних величин членів заданого знакопочережного ряду.
, складений з абсолютних величин членів заданого знакопочережного ряду.
Більш того, збіжним є і заданий знакопочережний ряд  , причому збігається він абсолютно.
, причому збігається він абсолютно.
Приклад 10. Дослідити на збіжність знакопочережний ряд

Розв’язання. Спочатку розглянемо ряд  , складений з абсолютних величин членів заданого ряду, і дослідимо його на збіжність. Застосуємо ознаку порівняння рядів. Для порівняння оберемо узагальнений гармонічний ряд
, складений з абсолютних величин членів заданого ряду, і дослідимо його на збіжність. Застосуємо ознаку порівняння рядів. Для порівняння оберемо узагальнений гармонічний ряд  , який є розбіжним
, який є розбіжним  . Оскільки
. Оскільки  , маємо
, маємо
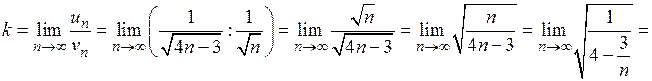
 – границя існує і
– границя існує і  .
.
Це означає, що поведінка порівнюваних рядів однакова, тобто ряд  , складений з абсолютних величин членів заданого ряду, є розбіжним, як і ряд, обраний для порівняння. При цьому питання про збіжність заданого знакопочережного ряду
, складений з абсолютних величин членів заданого ряду, є розбіжним, як і ряд, обраний для порівняння. При цьому питання про збіжність заданого знакопочережного ряду  залишається відкритим (!).
залишається відкритим (!).
Перевіримо, чи виконуються для цього ряду умови ознаки Лейбніца.
1) 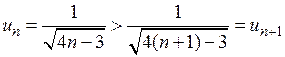 , тобто члени ряду спадають за абсолютною величиною – перша умова виконується.
, тобто члени ряду спадають за абсолютною величиною – перша умова виконується.
2)  – друга умова виконується теж.
– друга умова виконується теж.
Отже, за ознакою Лейбніца знакопочережний ряд  збіжний, але він збігається умовно, оскільки ряд з абсолютних величин його членів розбігається.
збіжний, але він збігається умовно, оскільки ряд з абсолютних величин його членів розбігається.
Приклад 11. Дослідити на збіжність знакопочережний ряд  .
.
Розв’язання. 1) Розглянемо спочатку ряд, складений з абсолютних величин членів заданого ряду, тобто ряд  , і дослідимо його на збіжність.
, і дослідимо його на збіжність.  загальний член цього ряду. Для порівняння обираємо гармонічний ряд
загальний член цього ряду. Для порівняння обираємо гармонічний ряд  , який розбігається. Оскільки загальний член останнього ряду
, який розбігається. Оскільки загальний член останнього ряду  , то за ознакою порівняння рядів маємо
, то за ознакою порівняння рядів маємо
 – границя існує і
– границя існує і  , що означає однакову поведінку рядів; тобто ряд
, що означає однакову поведінку рядів; тобто ряд  є розбіжним, як і ряд, обраний для порівняння.
є розбіжним, як і ряд, обраний для порівняння.
При цьому питання про збіжність заданого знакопочережного ряду  залишається відкритим (!).
залишається відкритим (!).
2) Перевіримо, чи виконуються для цього ряду умови ознаки Лейбніца. Щоб перевірити, чи спадають члени заданого ряду за абсолютною величиною, розглянемо допоміжну неперервну функцію 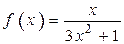 при
при  , яка при
, яка при  приймає значення
приймає значення  . Знайдемо похідну цієї функції:
. Знайдемо похідну цієї функції:
 .
.
При  похідна
похідна  ; отже, функція
; отже, функція 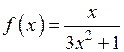 є спадною, тому спадною є і функція
є спадною, тому спадною є і функція  для
для 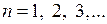
Отже, члени заданого ряду спадають за абсолютною величиною – перша умова ознаки Лейбніца виконується.
 – друга умова виконується теж.
– друга умова виконується теж.
За ознакою Лейбніца знакопочережний ряд  є збіжним, але він збігається умовно, оскільки ряд з абсолютних величин його членів розбігається.
є збіжним, але він збігається умовно, оскільки ряд з абсолютних величин його членів розбігається.
Приклад 12. Обчислити суму ряду  з точністю до
з точністю до  .
.
Розв’язання. Вище було доведено, що заданий знакопочережний ряд абсолютно збіжний (приклад 7). За ознакою Лейбніца він має суму S, яка не перевищує першого члена ряду  ;
;  . Розгорнемо скорочений запис ряду у суму
. Розгорнемо скорочений запис ряду у суму 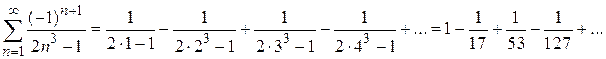
Оскільки при наближеному обчисленні суми збіжного знакопочережного ряду похибка співвідношення  не перевищує абсолютної величини першого з викреслених членів, то для забезпечення точності
не перевищує абсолютної величини першого з викреслених членів, то для забезпечення точності  достатньо залишити тільки три перших члена, поклавши
достатньо залишити тільки три перших члена, поклавши  , і викреслити всі наступні члени ряду, починаючи з четвертого. Дійсно,
, і викреслити всі наступні члени ряду, починаючи з четвертого. Дійсно,  .
.
Отже, сума ряду  з точністю до
з точністю до  .
.
1.2.Завдання для самостійного виконання
З а в д а н н я 1.1.
Для заданого ряду записати: а) чотири перших члена; б)  -й член.
-й член.
| 1.1.1. |  . .
| 1.1.2. |
 . .
| 1.1.3. | 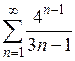 . .
|
| 1.1.4. |  . .
| 1.1.5. |  . .
| 1.1.6. |  . .
|
| 1.1.7. |  . .
| 1.1.8. |  . .
| 1.1.9. |  . .
|
| 1.1.10. |  . .
| 1.1.11. | 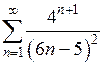 . .
| 1.1.12. |  . .
|
| 1.1.13. |  . .
| 1.1.14. |  . .
| 1.1.15. |  . .
|
| 1.1.16. |  . .
| 1.1.17. |  . .
| 1.1.18. |  . .
|
| 1.1.19. |  . .
| 1.1.20. |  . .
| 1.1.21. |  . .
|
| 1.1.22. |  . .
| 1.1.23. |  . .
| 1.1.24. |  . .
|
| 1.1.25. |  . .
| 1.1.26. |  . .
| 1.1.27. |  . .
|
З а в д а н н я 1.2.
1) Записати послідовність частинних сум  та визначити формулу для
та визначити формулу для  (
(  -ої частинної суми ряду).
-ої частинної суми ряду).
2) Знайти  та зробити висновок про збіжність або розбіжність ряду.
та зробити висновок про збіжність або розбіжність ряду.
| 1.2.1.* | 
|
| 1.2.2.* | 
|
| 1.2.3.* | 
|
| 1.2.4.* | 
|
| 1.2.5.* | 
|
З а в д а н н я 1.3.
Підібрати одну з можливих формул загального члену ряду, перші члени якого задано:
| 1.3.1.* | 
| 1.3.2.* | 
| |
| 1.3.3.* | 
| 1.3.4.* | 
| |
| 1.3.5.* | 
| 1.3.6.* | 
| |
| 1.3.7.* | 
| 1.3.8.* | 
| |
| 1.3.9.* | 
| 1.3.10.* | 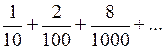
| |
| 1.3.11.* | 
| 1.3.12.* | 
| |
| 1.3.13.** | 
| 1.3.14.** | 
| |
| 1.3.15.** | 
| 1.3.16.** | 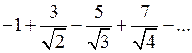
|
З а в д а н н я 1.4.
Дослідити на збіжність числові ряди:
| 1.4.1. |
а)  ; ;
| б)  ; ;
| |
в) 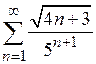 ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.2. | а) 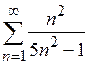 ; ;
|
б)  ; ;
| |
в)  ; ;
| г) 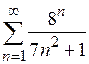 ; ;
| д)* 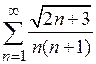 . .
| |
| 1.4.3. |
а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.4. |
а) 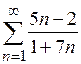 ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.5. |
а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.6. | а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.7. |
а)  ; ;
| б)  ; ;
| |
в)  ; ;
| г)*  ; ;
| д)* 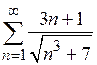 . .
| |
| 1.4.8. | а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.9. |
а)  ; ;
| б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.10. |
а)  ; ;
|
б) 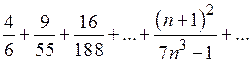 ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.11. |
а) 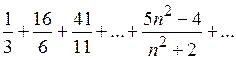 ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.12. | а)  ; ;
|
б) 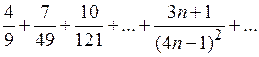 ; ;
| |
в)  ; ;
| г)  ; ;
| д)* 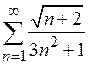 . .
| |
| 1.4.13. |
а)  ; ;
| б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.14. | а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.15. |
а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.16. | а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)* 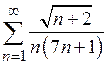 . .
| |
| 1.4.17. |
а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.18. | а)  ; ;
|
б)  ; ;
| |
в) 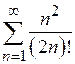 ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.19. |
а) 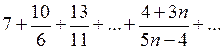 ; ;
| б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.20. | а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.21. |
а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)* 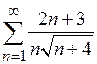 . .
| |
| 1.4.22. | а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.23. |
а)  ; ;
|
б) 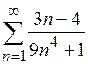 ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.24. | а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
| |
| 1.4.25. |
а)  ; ;
|
б)  ; ;
| |
в)  ; ;
| г)  ; ;
| д)*  . .
|
З а в д а н н я 1.5.
Дослідити на абсолютну та умовну збіжність ряди:
| 1.5.1. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.2. |
а) 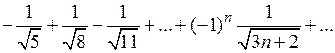 ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.3. |
а)  ; ;
| |
б)  ; ;
| в)* 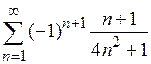 . .
| |
| 1.5.4. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.5. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.6. |
а)  ; ;
| |
б) 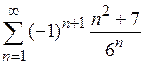 ; ;
| в)*  . .
| |
| 1.5.7. |
а)  ; ;
| |
б)  ; ;
| в)* 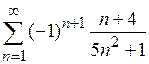 . .
| |
| 1.5.8. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.9. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.10. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.11. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.12. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.13. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.14. |
а)  ; ;
| |
б)  ; ;
| в)* 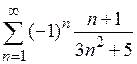 . .
| |
| 1.5.15. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.16. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.17. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.18. |
а) 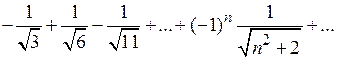 ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.19. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.20. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.21. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.22. |
а)  ; ;
| |
б) 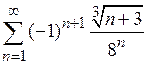 ; ;
| в)*  . .
| |
| 1.5.23. |
а)  ; ;
| |
б)  ; ;
| в)* 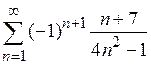 . .
| |
| 1.5.24. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
| |
| 1.5.25. |
а)  ; ;
| |
б)  ; ;
| в)*  . .
|
З а в д а н н я 1.6.
1) Обчислити суму 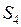 перших чотирьох членів збіжного знакопочережного ряду та оцінити похибку, яка виникає, якщо вважати, що
перших чотирьох членів збіжного знакопочережного ряду та оцінити похибку, яка виникає, якщо вважати, що  .
.
2) Обчислити суму цього ряду з точністю до 0,001.
| 1.6.1. |  . .
| 1.6.2. |  . .
|