Главная | Обратная связь

Полиномиальные коды

При полиномиальном кодировании каждое сообщение отождествляется с многочленом, а само кодирование состоит в умножении на фиксированный многочлен. Полиномиальные коды - блочные и отличаются от рассмотренных ранее только алгоритмами кодирования и декодирования.

Пусть - двоичное сообщение. Тогда сопоставим ему многочлен . Все вычисления происходят в поле классов вычетов по модулю 2, т. е. от результата любой арифметической операции берется остаток от его деления на 2.

Например, последовательности 10011 при соответствует многочлен .

Зафиксируем некоторый многочлен степени ,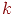

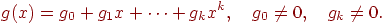
Полиномиальный код с кодирующим многочленом кодирует слово сообщения многочленом или кодовым словом из коэффициентов этого многочлена . Условия и необходимы, потому что в противном случае и не будут нести никакой информации, т.к. они всегда будут нулями.

Пример. Рассмотрим кодирующий многочлен . Сообщение 01011, отвечающее многочлену 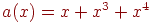, будет закодировано коэффициентами многочлена , т.е. .

Полиномиальный код с кодирующим многочленом степени 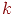является матричным кодом с кодирующей матрицей размерности :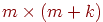

Т е. ненулевые элементы в -й строке - это последовательность коэффициентов кодирующего многочлена, расположенных с -го по -й столбцах.

Например, 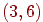-код с кодирующим многочленом отвечает матрице

или отображению: ; ; ; ; ; ; ; .

Полиномиальные коды являются групповыми.

Это следует из того, что коды, получаемые матричным кодированием, - групповые.

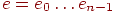Рассмотрим -код с кодирующим многочленом . Строка ошибок останется необнаруженной в том и только в том случае, если соответствующий ей многочлен делится на .

Действительно, 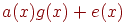делится на тогда и только тогда, когда делится на . Поэтому любая ошибка, многочлен которой не делится на , будет обнаружена и, соответственно, любая ошибка, многочлен которой делится на , не может быть обнаружена.

Таким образом, обнаружение ошибки при использовании полиномиального кода с кодирующим многочленом может быть реализовано при помощи алгоритма деления многочленов с остатком: если остаток ненулевой, то при передаче произошло искажение данных.

Коды Хэмминга можно строить как полиномиальные, например, кодирующий многочлен определяет совершенный 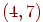-код, отличный от рассмотренного ранее.

Вообще же, если кодирующий многочлен , порождающий соответствующий -код, не является делителем ни одного из многочленов вида 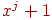при , то минимальное расстояние между кодовыми словами порожденного им кода не меньше 3.

Пусть - минимальное расстояние между кодовыми словами, оно равно минимуму среди весов ненулевых кодовых слов. Предположим . Тогда существует такой, что и степень не больше . Вес равен 2, поэтому и . Следовательно, , что означает, что должен делиться на , а это невозможно по условию. Если предположить, что , то это приведет к утверждению о том, что должен делиться на , что тоже противоречит условию. Итак, .

Кодирующий многочлен определяет совершенный -код Голея (Golay) с минимальным расстоянием между кодовыми словами 7.

В 1971 году финскими и советскими математиками было доказано¹⁾, что кроме кодов Хэмминга и Голея других совершенных кодов нет.

Наиболее интересными среди полиномиальных кодов являются циклические коды, в которых вместе с любым кодовым словом вида есть кодовое слово .

Упражнение 43 По кодирующему многочлену построить полиномиальные коды для двоичных сообщений 0100, 10001101, 11110.

Упражнение 44 Принадлежат ли коду Голея кодовые слова 10000101011111010011111 и 11000111011110010011111?