Главная | Обратная связь

Лінійні диференціальні рівняня другого порядку зі сталими коефіцієнтами.

Ці рівняння мають вигляд:

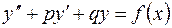, де p, q - є дійсні числа.

Якщо , то маємо однорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами, а саме:

.

Загальний інтеграл такого рівняння має вигляд:

,

де та є лінійно незалежні фундаментальні роз’вязки цього рівняння, вигляд яких визначається в залежності від коренів відповідного характеристичного рівняння.

Характеристичне рівняння, що відповідає однорідному диференціальному рівнянню, має вигляд:

,

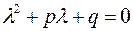яке складається виходячи з заданого однорідного диференціального рівняння за наступним правилом: другій похідній відповідає квадрат деякої невідомої 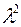, перший похідній відповідає змінна в першому степені , а функції відповідає змінна в нульовому степені, а коефіцієнти переносяться без змін.

Якщо характеристичне рівняння має дійсні різні корені та , то фундаментальні роз’вязки мають вигляд:

, ,

та загальний інтеграл такого однорідного диференціального рівняння є^

.

Якщо характеристичне рівняння має кратні дійсні корені , то загальний інтеграл однорідного диференціального рівняння є

.

Якщо характеристичне рівняння має комплексно сполучені корені:

, , тоді:

.

Задача 9.7. Визначити загальний інтеграл рівняння

.

Розв’язання. Складемо характеристичне рівняння та визначимо його корені. Маємо:

,

що видно за теоремою Вієта.

Тоді рішення диференціального рівняння, яке подано до розгляду, має вигляд:

.

Задача 9.8. Визначити загальний інтеграл рівняння

.

Розв’язання. Маємо характеристичне рівняння

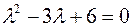, та ; .

Тоді загальний інтеграл має вигляд:

Розглянемо лінійне неоднорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами:

.

Загальний інтеграл такого рівняння має вигляд: , де Y – є загальний інтеграл (загальне рішення) відповідного однорідного диференціального рівняння, а - є частковий інтеграл (часткове рішення ) неоднорідного диференціального рівняння.

Часткове рішення визначається в залежності від типу правої частини неоднорідного диференціального рівняння. Так, наприклад:

1. Якщо , де - довільний многочлен та не співпадає з коренями та характеристичного рівняння, то

,

де - є многочлен, степінь якого співпадає із степеню многочлена , та має коефіцієнти, які визначаються за методом невизначених коефіцієнтів.

2. Якщо та є простий корінь характеристичного рівняння, то

.

3. Якщо та є кратний корінь характеристичного рівняння, то

.

Задача 9.9. Визначити загальний інтеграл диференціального рівняння .

Розв’язання. Подане до розв’язку диференціальне рівняння є лінійним неоднорідним диференціальним рівнянням другого порядку зі сталими коефіцієнтами та праву частину спеціального вигляду, а саме права частина складається з многочлена та степеневої функції.

Характеристичне рівняння відповідного однорідного диференціального рівняння:

, тоді ; ,

тобто корінь характеристичного рівняння є кратним, тому загальне рішення однорідного диференціального рівняння має вигляд:

.

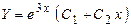При визначені часткового рішення неоднорідного диференціального рівняння звернемо увагу на те, що , як уже відзначалось, є сума многочлена та добутку многочлена на степеневу функцію , тому часткове рішення буде також складатись із суми двох відповідних часткових рішень: , де ; , де 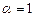та не є коренем характеристичного рівняння, тобто . Визначимо коефіцієнти А, В, С.

Для цього знайдемо першу та другу похідні у: ; , тоді, після підстановки в рівняння, отримаємо:

;

;

.

Порівнюючи коефіцієнти при , отримаємо , , .

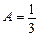Тому:

,

і загальний розв’язок неоднорідного диференціального рівняння має вигляд:

.

У випадку, коли права частина містить функції вигляду: cosβx, або sinβx, діють подібним до попереднього чином.

Задача 9.10. Визначити загальне рішення диференціального рівняння .

Розв’язання. Загальне рішення . де Y – загальне рішення відповідного однорідного диференціального рівняння, а – часткове рішення неоднорідного диференціального рівняння.

Маємо, що однорідне рівняння 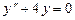, а йому відповідне характеристичне рівняння , корені якого , має загальне рішення

.

Права частина рівняння: , дає підстави часткове рішення визначати як , де – часткове рішення, яке визначається , а – часткове рішення, яке визначається 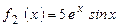. Маємо , так як та не є коренем характеристичного рівняння, , так як не є коренем характеристичного рівняння.

Тоді .

Визначимо загальне рішення даного рівняння. Маємо:

.

Для визначення коефіцієнтів А, В та С прийдемо до системи рівнянь:

;

;

;

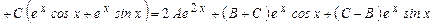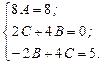
Маємо ; ; .

Тоді загальне рішення неоднорідного диференціального рівняння має вигляд:

.

Доцільно відзначити, що при необхідності розв’язання диференціального рівняння послідовність формування міркувань щодо його роз’вязання може відповідати наступній послідовності. Перш за все, слід визначити порядок диференціального рівняння. Якщо воно є звичайним диференціальним рівнянням першого порядку, то, в подальшому, необхідно з’ясувати його тип: чи воно є рівнянням, яке допускає відокремлювання змінних; чи є однорідним відносно незалежної змінної та шуканої функції, чи воно є лінійним, чи воно є рівнянням Бернуллі. Якщо задане диференціальне рівняння є диференціальним рівнянням другого порядку, то необхідно з’ясувати його тип: диференціальне рівняння, що допускає зниження порядку; лінійне однорідне зі сталими коефіцієнтами чи лінійне неоднорідне зі сталими коефіцієнтами. Після цього застосувати відповідні способи визначення його розв’язку.