 |
|
Необхідна ознака збіжності числового ряду
Розділ 8. РЯДИ
Поняття суми скінченої кількості чисел і її властивості відомі ще з давніх часів. Шукаючи суму геометричної прогресії, математик і механік Стародавньої Греції Архімед зустрівся з нескінченними рядами.
Для детального вивчення функції рядами систематично користувались англійський математик, механік, фізик, астроном І.Ньютон та великі німецькі вчені Г.Лейбніц і К. Гаусс.
Однак точна теорія рядів, в основі якої лежали поняття границі послідовності, була побудована на початку 19 ст. французьким математиком О.Коші. З цього часу ряди стали основним джерелом дослідження в математиці. З’явились цілі розділи математики, повністю побудовані на теорії рядів.
Методи цього розділу застосовуються для знаходження наближених значень інтегралів, які часто зустрічаються в теорії ймовірностей та у страховій справі, і не можуть бути виражені елементарними функціями; при розв’язуванні диференціальних рівнянь; при знаходженні наближених значень функцій, які використовуються при розв’язуванні економічних задач.

§1. Числовий ряд та його збіжність.
Ряд геометричної прогресії
Нехай задана нескінченна послідовність чисел
 ....
....
Означення. Нескінченна сума чисел виду
 називається числовим рядом, а
називається числовим рядом, а  - членами ряду.
- членами ряду.
Коротко ряд записується так:  . Вираз для
. Вираз для  го члена ряду при довільному натуральному
го члена ряду при довільному натуральному 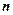 , називається загальним членом цього ряду і позначається
, називається загальним членом цього ряду і позначається 
Ряд вважається заданим, якщо відомо правило , за яким для довільного номера 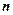 можна записати відповідний член ряду. Загальний член ряду можна задати формулою un=f(n), з допомогою якої записується довільний член ряду.
можна записати відповідний член ряду. Загальний член ряду можна задати формулою un=f(n), з допомогою якої записується довільний член ряду.
Наприклад, якщо 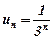 , то ряд матиме відповідно вигляд
, то ряд матиме відповідно вигляд
 .
.
Якщо ряд записано у вигляді  , то легко записати декілька його членів.
, то легко записати декілька його членів.
Наприклад, якщо задано ряд  , то в іншій формі він матиме вигляд
, то в іншій формі він матиме вигляд 
Якщо відомо декілька членів числового ряду, то зрозумівши закономірність їх утворення, можна записати загальний член ряду.
Наприклад, задано чотири перших члени ряду
 .
.
Як бачимо, чисельники кожного члена ряду є натуральними числами. Знаменник першого члена ряду 100=1. Кожен знаменник наступного члена більший від попереднього в 10 разів. Таким чином, загальний член ряду записуємо  .
.
Нехай задано ряд  (8.1)
(8.1)
Суму n перших його членів позначимо через Sn:
 (8.2)
(8.2)
і назвемо n-ою частинною сумою ряду.
Утворимо тепер послідовність частинних сум ряду:

Означення. Якщо при n®¥ існує границя послідовності частинних сум  членів даного ряду
членів даного ряду  , то ряд називається збіжним, а число S - його сумою.
, то ряд називається збіжним, а число S - його сумою.
Записують це так:
 (8.3)
(8.3)
Якщо послідовність частинних сум  не має границі, то ряд називається розбіжним.
не має границі, то ряд називається розбіжним.
Ряд може розбігатися у двох випадках:
1)  ;
;
2) Послідовність  коливається.
коливається.
Як приклад розглянемо ряд нескінченної геометричної прогресії:
 (8.4)
(8.4)
Сума 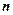 перших членів прогресії рівна
перших членів прогресії рівна 
Якщо  , то
, то  і тому
і тому

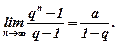
Отже, якщо  ,то нескінченна геометрична прогресія утворює збіжний ряд, сума якого
,то нескінченна геометрична прогресія утворює збіжний ряд, сума якого 
Якщо  , то
, то  тому
тому  , і ряд геометричної прогресії розбігається.
, і ряд геометричної прогресії розбігається.
При  одержимо ряд
одержимо ряд  , який має частинну суму
, який має частинну суму  і
і 
Якщо  , одержимо ряд
, одержимо ряд 
Його частинні суми набирають таких значень: 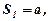


 , тобто
, тобто  коливна послідовність, яка не має границі.
коливна послідовність, яка не має границі.
Наслідок. Якщо ряд (8.1) збігається, то різниця між сумою  і частинною сумою
і частинною сумою  його
його
 (8.5)
(8.5)
називається 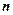 -им залишком ряду.
-им залишком ряду.
Залишок Rn ряду являє собою ту похибку, яка одержиться, якщо замість наближеного значення суми ряду S взяти суму Sn перших n членів цього ряду. Але оскільки S є границя змінної Sn, то очевидно , 
А тому, взявши достатньо велике число членів збіжного ряду, можна суму цього ряду обчислити з любою точністю.
Звідси випливає, що основною задачею теорії рядів є дослідження збіжності ряду.
В наступному прикладі покажемо застосування ряду нескінченно спадної геометричної прогресії в економічних дослідженнях.
Приклад.Нехай I0- початкові інвестиції, вкладені в замкнуту економічну систему, а q- доля національного доходу, яка йде на споживання, то в моделі Кейнса  вартість національного прибутку
вартість національного прибутку  виражається формулою
виражається формулою
 . (8.6)
. (8.6)
Права частина рівності (8.6) є не що інше як сума ряду нескінченно спадної геометричної прогресії із знаменником 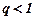 і
і
 . (8.7)
. (8.7)
Ця формула може бути використана для знаходження зміни вартості національного прибутку в залежності від початкових інвестицій  та її долі
та її долі  , що йде на споживання.
, що йде на споживання.
Гармонічний ряд
Ряд  (8.8)
(8.8)
називається гармонічним.
Доведемо розбіжність цього ряду. Скористаємося тим, що змінна  при необмеженому зростанні n прямує до неперового числа e, залишаючись меншим своєї границі. Тому при
при необмеженому зростанні n прямує до неперового числа e, залишаючись меншим своєї границі. Тому при
любому цілому додатному 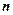 маємо
маємо 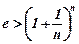 .
.
Звідси  або
або  або
або 
Підставляючи в останню нерівність замість 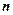 числа 1,2,3,... одержимо нерівності:
числа 1,2,3,... одержимо нерівності:

Додавши почленно ці нерівності, одержимо
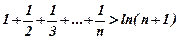 або
або 
Але  а тому і
а тому і  тобто ряд (8.8) розбігається.
тобто ряд (8.8) розбігається.
Необхідна ознака збіжності числового ряду
ТЕОРЕМА. Якщо ряд
 (8.9),
(8.9),
збігається, то його 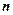 -ий член
-ий член  при необмеженому зростанні номера
при необмеженому зростанні номера 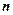 прямує до нуля.
прямує до нуля.
Доведення. Ми маємо  і
і
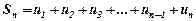 . Звідси
. Звідси  . Оскільки
. Оскільки
даний ряд збігається, то  і
і  . Звідси
. Звідси
 що і
що і