 |
|
Абсолютна та умовна збіжність ряду
Розглянемо знакозмінний ряд, у якому члени з додатними і від’ємними знаками не обов’язково чергуються. Позначимо такий ряд  , де
, де  - числа як додатні, так і від’ємні.
- числа як додатні, так і від’ємні.
Складаємо ряд з абсолютних величин його членів:
 .
.
Якщо ряд з абсолютних величин збігається, то знакозмінний ряд називається абсолютно збіжним. Якщо знакозмінний ряд збігається, а ряд, складений з абсолютних величин, розбігається, то знакозмінний ряд називається неабсолютно збіжним (або умовно збіжним).
ТЕОРЕМА. Якщо ряд, складений із абсолютних величин членів даного ряду, збігається, то збігається і даний ряд.
Доведення. Позначимо через  суму
суму  перших членів ряду
перших членів ряду  (8.21)
(8.21)
через  - суму всіх додатних членів, а через
- суму всіх додатних членів, а через  - суму абсолютних величин всіх від’ємних членів серед перших
- суму абсолютних величин всіх від’ємних членів серед перших  членів ряду.
членів ряду.
Тоді  і
і 
 , (8.22)
, (8.22)
де 
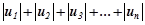 .
.
Оскільки згідно з умовою 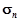 має границю, тобто
має границю, тобто  , a
, a  і
і  - додатні і зростаючі функції від
- додатні і зростаючі функції від  , причому
, причому  і
і  , то і вони мають границі. А отже і
, то і вони мають границі. А отже і  при
при  прямує до границі, що і потрібно було довести.
прямує до границі, що і потрібно було довести.
Це достатня ознака, але не є необхідною, тобто ряд  може збігатися і тоді, коли ряд
може збігатися і тоді, коли ряд  розбігається.
розбігається.
Приклад 1.Дослідити збіжність ряду
 .
.
Розв’язування. Даний ряд називають рядом Лейбніца. Оскільки 
 , то даний ряд збігається (згідно з ознакою Лейбніца). Ряд, складений із абсолютних величин
, то даний ряд збігається (згідно з ознакою Лейбніца). Ряд, складений із абсолютних величин  є гармонічним, який, як відомо, розбіжний. Отже, даний ряд Лейбніца умовно збіжний.
є гармонічним, який, як відомо, розбіжний. Отже, даний ряд Лейбніца умовно збіжний.
Приклад 2.Дослідити збіжність ряду  .
.
Розв’язування. Складемо ряд з абсолютних величин

Він збігається як ряд нескінченно спадної геометричної прогресії із знаменником 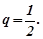 Отже заданий ряд збігається абсолютно.
Отже заданий ряд збігається абсолютно.
Поняття про степеневий ряд та його збіжність
Ряд, членами якого є функції змінної  , називається
, називається
Функціональним.
Це ряд вигляду
 (8.23)
(8.23)
Якщо  набуває будь-якого числового значення, то ряд (8.23) стає числовим.
набуває будь-якого числового значення, то ряд (8.23) стає числовим.
Сукупність всіх значень змінної  , при яких функціональний ряд збігається, називається областю збіжності цього ряду. Будемо розглядати ряди, областями збіжності яких служать різні інтервали осі Ox.
, при яких функціональний ряд збігається, називається областю збіжності цього ряду. Будемо розглядати ряди, областями збіжності яких служать різні інтервали осі Ox.
Якщо для всякого значення  із інтервалу
із інтервалу  функціональний ряд збігається, то його сума є функція
функціональний ряд збігається, то його сума є функція
 (8.24)
(8.24)
Інакше кажучи, функція  в інтервалі
в інтервалі  розкладається в ряд.
розкладається в ряд.
Степеневим рядом називається функціональний ряд виг- ляду 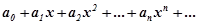 ,(8.25)
,(8.25)
де 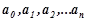 - постійні числа.
- постійні числа.
Іноді розглядають степеневий ряд більш загального вигляду:
 , (8.26)
, (8.26)
де  - деяке постійне число. Останній ряд легко приводиться до попереднього степеневого ряду, якщо перепозначити
- деяке постійне число. Останній ряд легко приводиться до попереднього степеневого ряду, якщо перепозначити  .
.
Доведемо досить важливу теорему на якій буде базуватися вивчення степеневих рядів.
ТЕОРЕМА Абеля. Якщо степеневий ряд (8.25) збігається в точці  , то він збігається абсолютно в інтервалі
, то він збігається абсолютно в інтервалі  , тобто при всякому
, тобто при всякому  , що задовольняє умові
, що задовольняє умові 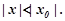
Доведення. Із збіжності ряду (8.25) в точці  випливає, що його загальний член
випливає, що його загальний член  при
при  А тому всі члени цього ряду є обмежені, тобто існує таке постійне додатне число
А тому всі члени цього ряду є обмежені, тобто існує таке постійне додатне число  , що для всякого
, що для всякого  має місце нерівність
має місце нерівність
 .
.  (8.27)
(8.27)
Запишемо ряд (8.25) так:
 (8.28)
(8.28)
і складемо ряд із абсолютних величин членів цього ряду:
 (8.29)
(8.29)
В силу установленої нерівності (8.27) кожний член ряду (8.29) менший відповідного члена геометричної прогресії із знаменником
 :
:
 (8.30)
(8.30)
Якщо  , то
, то  і ряд (8.30) збігається; а тому збігається і ряд абсолютних величин (8.29), а значить, абсолютно збігається сам ряд (8.25). Теорема доведена.
і ряд (8.30) збігається; а тому збігається і ряд абсолютних величин (8.29), а значить, абсолютно збігається сам ряд (8.25). Теорема доведена.
Наслідок. Якщо степеневий ряд (8.25) розбігається при 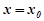 , то він розбігається і при всякому
, то він розбігається і при всякому  більшому за абсолютною величиною, ніж
більшому за абсолютною величиною, ніж  , тобто при
, тобто при 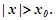
Таким чином можна стверджувати, що для будь-якого степеневого ряду, який має як точки збіжності так і точки розбіжності, існує таке додатне число  , що для всіх
, що для всіх  , по модулю менших
, по модулю менших  ряд абсолютно збігається, а для всіх
ряд абсолютно збігається, а для всіх  , по модулю більших
, по модулю більших  ряд розбігається. Число
ряд розбігається. Число  називається радіусом збіжності степеневого ряду (8.25). Інтервал
називається радіусом збіжності степеневого ряду (8.25). Інтервал  називається інтервалом збіжності. Якщо
називається інтервалом збіжності. Якщо  то інтервал збіжності вироджується в точку, а при
то інтервал збіжності вироджується в точку, а при  - у всю числову вісь.
- у всю числову вісь.
Для степеневих рядів (8.26) все сказане вище залишається в силі, лише з тією різницею, що тепер центр інтервалу збіжності буде лежати не в точці 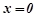 , а в точці
, а в точці  . А отже, інтервалом збіжності буде
. А отже, інтервалом збіжності буде 
В наступній теоремі буде дано спосіб відшукання радіуса збіжності степеневого ряду.
ТЕОРЕМА . Якщо існує 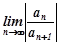 , то радіус збіжності степеневого ряду знаходиться за формулою
, то радіус збіжності степеневого ряду знаходиться за формулою
 (8.31)
(8.31)
Доведення. Складемо ряд із абсолютних величин членів ряду (8.25): 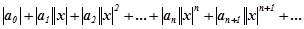 (8.32)
(8.32)
З попереднього параграфа відомо, що якщо збігається ряд (8.32), то збігається ряд (8.25) абсолютно. Припустивши, що  , одержимо
, одержимо  .
.
Згідно з ознакою Даламбера, ряд (8.32) збігається, якщо  , тобто , якщо
, тобто , якщо  , і розбігається, якщо
, і розбігається, якщо

Отже, степеневий ряд (8.25) збігається, для всіх тих значень  , для яких
, для яких  , і розбігається для тих значень
, і розбігається для тих значень  , для яких
, для яких  .
.
Таким чином, для ряду (8.25), радіус збіжності знаходиться за формулою 
Приклад 1. Знайти інтервал збіжності степеневого ряду
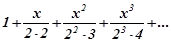 і дослідити його збіжність на кінцях інтервалу.
і дослідити його збіжність на кінцях інтервалу.
Розв’язування. Тут  ,
,  .
.
Знаходимо радіус збіжності ряду
 Отже, ряд збігається в інтервалі
Отже, ряд збігається в інтервалі  . Щоб вирішити питання про збіжність степеневого ряду на кінцях інтервалу, покладемо спочатку х=2. Отримаємо гармонічний ряд
. Щоб вирішити питання про збіжність степеневого ряду на кінцях інтервалу, покладемо спочатку х=2. Отримаємо гармонічний ряд  який, як відомо, розбігається. При
який, як відомо, розбігається. При  одержимо знакозмінний ряд Лейбніца:
одержимо знакозмінний ряд Лейбніца:
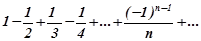 .
.
Цей ряд збігається умовно. Таким чином, степеневий ряд збігається для  .
.
Приклад 2. Знайти інтервал збіжності степеневого ряду
 і дослідити його збіжність на кінцях інтервалу.
і дослідити його збіжність на кінцях інтервалу.
Розв’язування. Оскільки  ,
, 
 радіус збіжності
радіус збіжності
 Отже , даний ряд абсолютно збігається в інтервалі
Отже , даний ряд абсолютно збігається в інтервалі 
Дослідимо степеневий ряд на кінцях інтервалу, тобто в точках 
При  отримуємо числовий ряд
отримуємо числовий ряд  .
.
Для дослідження збіжності ряду використаємо інтегральну ознаку Коші. Для цього обчислимо інтеграл
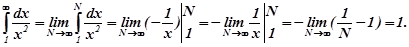 Невласний інтеграл збігається , значить, і числовий ряд теж збігається, тобто правий кінець входить в інтервал збіжності.
Невласний інтеграл збігається , значить, і числовий ряд теж збігається, тобто правий кінець входить в інтервал збіжності.
При  одержимо числовий ряд
одержимо числовий ряд
 який збігається абсолютно, тому що виконуються умови ознаки Лейбніца:
який збігається абсолютно, тому що виконуються умови ознаки Лейбніца:  ;
; 
 і збігається ряд , складений з абсолютних величин. Таким чином, вихідний степеневий ряд абсолютно збігається на відріз- ку
і збігається ряд , складений з абсолютних величин. Таким чином, вихідний степеневий ряд абсолютно збігається на відріз- ку 
Приклад 3. Знайти інтервал збіжності степеневого ряду
 .
.
Розв’язування. Оскільки  ,
,  ,
,
то 
Це означає, що ряд збігається тільки при  і розбігається при інших значеннях.
і розбігається при інших значеннях.
Приклад 4. Знайти інтервал збіжності степеневого ряду
 .
.
Розв’язування. Тут  ,
,  ,
,

Значить, ряд збігається, якщо  , тобто інтервал збіжності степеневого ряду
, тобто інтервал збіжності степеневого ряду  .
.
Дослідимо збіжність степеневого ряду на кінцях інтервалу збіжності. При  одержимо ряд
одержимо ряд  .
.
Даний ряд збігається, оскільки, згідно з інтегральною ознакою Коші, невласний інтеграл

є збіжним.
Якщо  , то одержимо знакозмінний ряд
, то одержимо знакозмінний ряд  .
.
Цей ряд збігається, оскільки виконуються умови ознаки Лейбніца:
1)  , 2)
, 2) 