 |
|
ТЕОРЕМА 2. Степеневий ряд
Диференціювання та інтегрування степеневих рядів.
Розклад деяких функцій в степеневі ряди
Приведемо дві важливі теореми (без доведення).
ТЕОРЕМА 1. Степеневий ряд
 (8.33)
(8.33)
І одержаний із нього почленним диференціюванням ряд
 (8.34)
(8.34)
мають один і той же інтервал збіжності  Сума ряду (8.34) дорівнює похідній
Сума ряду (8.34) дорівнює похідній  суми
суми 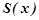 ряду (8.33) при всіх значеннях
ряду (8.33) при всіх значеннях  , для яких
, для яких  .
.
ТЕОРЕМА 2. Степеневий ряд
 (8.35)
(8.35)
і ряд  (8.36)
(8.36)
одержаний із ряду (8.35) почленним інтегруванням, мають однаковий інтервал збіжності. Сума ряду (8.36) дорівнює  де
де 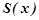 - сума ряду (8.35).
- сума ряду (8.35).
Для практики важливо вміти дану функцію 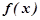 розкласти в степеневий ряд, тобто функцію
розкласти в степеневий ряд, тобто функцію 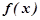 представити у вигляді степеневого ряду, що дає можливість досить просто обчислювати значення цієї функції.
представити у вигляді степеневого ряду, що дає можливість досить просто обчислювати значення цієї функції.
Спочатку розглянемо деякі часткові випадки. Розглянемо степеневий ряд
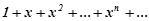 . (8.37)
. (8.37)
Цей ряд являє собою ряд геометричної прогресії із знаменником  , який збіжний при
, який збіжний при  і його сума рівна
і його сума рівна  .
.
Отже, ми можемо записати:
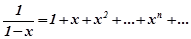 (8.38)
(8.38)
На останню рівність можна дивитися як на розклад функції  в степеневий ряд. Із розкладу (8.38) можна легко одержати інші розклади функцій.
в степеневий ряд. Із розкладу (8.38) можна легко одержати інші розклади функцій.
Розклад функції  .
.
Замінивши в розкладі (8.38)  на
на  , будемо мати:
, будемо мати:
 . (8.39)
. (8.39)
Якщо 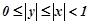 , то рівність (8.39), як було сказано в попередньому параграфі, можна проінтегрувати почленно по
, то рівність (8.39), як було сказано в попередньому параграфі, можна проінтегрувати почленно по  в межах від 0 до
в межах від 0 до  , тобто
, тобто 
Звідси маємо: 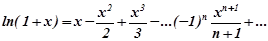 ,
,  <1.
<1.
Такий розклад справедливий також для  і відповідно ряд
і відповідно ряд
 є збіжним. Область збіжності буде множина
є збіжним. Область збіжності буде множина 
 .
.
Розклад функції 
Покладемо в розкладі (8.38) 
 (8.40)
(8.40)
Помноживши останню рівність на  і проінтегрувавши почленно в межах від 0 до
і проінтегрувавши почленно в межах від 0 до  , де
, де 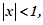 одержимо:
одержимо:
 або
або
 .
.
Оскільки  то маємо:
то маємо:
 , якщо
, якщо  <1. (8.41)
<1. (8.41)
Можна довести, що цей розклад є справедливим при  і
і 
При  маємо:
маємо: 
 .
.
При  маємо:
маємо: 
 .
.
Отже, область збіжності даного степеневого ряду буде відрізок  .
.
Ми бачимо, що деякі функції, як, наприклад  ,
,  і тому подібні, допускають розклад в степеневий ряд відносно аргументу
і тому подібні, допускають розклад в степеневий ряд відносно аргументу  . Природно поставити загальне питання про розклад даної функції
. Природно поставити загальне питання про розклад даної функції 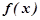 по зростаючим цілим додатнім степеням
по зростаючим цілим додатнім степеням  . Цим питанням ми займемось в наступному параграфі.
. Цим питанням ми займемось в наступному параграфі.
§ 9. Розклад функції в ряд Маклорена
Припустимо, що дана функція 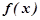 може бути розкладена в степеневий ряд
може бути розкладена в степеневий ряд 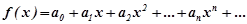 , (8.42)
, (8.42)
де  - невизначені коефіцієнти, причому інтервал збіжності
- невизначені коефіцієнти, причому інтервал збіжності 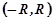 не зводиться до точки, тобто
не зводиться до точки, тобто  .
.
Як було сказано вище, степеневий ряд (8.42) в його інтервалі збіжності можна диференціювати почленно будь-яке число раз, причому всі одержані ряди будуть збігатися і їх суми будуть дорівнювати відповідним похідним від суми даного ряду 
Продиференціювавши почленно ряд (8.42)  раз , будемо мати:
раз , будемо мати:
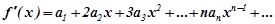 ,
,


 .
.
Поклавши в цих рівностях, включаючи (8.42), х=0 одержимо:



 ;
; 
Звідси 



 .
.
Підставивши значення коефіцієнтів  в (8.42), одержимо формулу Маклорена:
в (8.42), одержимо формулу Маклорена:
 , (8.43)
, (8.43)
де  (
(  ) – залишковий член у формі Лагранжа. Число
) – залишковий член у формі Лагранжа. Число  можна записати у вигляді
можна записати у вигляді  ,
, 
Якщо при необмеженому зростанні n, тобто при 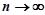
 (8.44)
(8.44)
то із формули Маклорена одержимо розклад функції 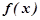 в ряд по степенях
в ряд по степенях  , який називається рядом Маклорена:
, який називається рядом Маклорена:
 (8.45)
(8.45)
А умова (8.44) являє собою необхідну і достатню умову того, що ряд Маклорена для функції 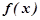 , яка диференційована необмежене число разів, збігається до цієї функції.
, яка диференційована необмежене число разів, збігається до цієї функції.
Приведемо приклади на застосування ряду Маклорена до розкладу деяких елементарних функцій в степеневі ряди.
Розклад функції 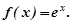
Нехай  Тоді
Тоді 
 …
… 
Поклавши  , одержимо:
, одержимо:
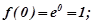

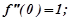 …
… 
Підставивши ці значення в формулу Маклорена (8.43) , будемо мати:
 ,
,
де 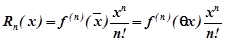 .
.
Оскільки  - величина обмежена при обмеженому
- величина обмежена при обмеженому 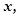 то, для того, щоб довести, що
то, для того, щоб довести, що  , потрібно показати,що
, потрібно показати,що  . Для того зафіксуємо
. Для того зафіксуємо  і розглянемо ряд
і розглянемо ряд 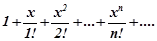
Якщо він збігається, то його загальний член  при
при 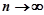 прямує до нуля. Використаємо ознаку Даламбера до ряду абсолютних величин:
прямує до нуля. Використаємо ознаку Даламбера до ряду абсолютних величин:

Отже,  .
.
Таким чином  і функція
і функція  розкладається в інтервалі
розкладається в інтервалі  в слідуючий ряд Маклорена
в слідуючий ряд Маклорена
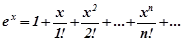 (8.46)
(8.46)
Розклад функцій 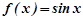 ,
, 
Нехай 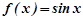 ; звідси
; звідси
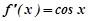 ,
,  ,
,  ,
, 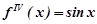 ,…
,…
Поклавши х=0, маємо :


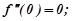

 …
…
Підставивши ці значення у формулу (8.45), одержимо:
 . (8.47)
. (8.47)
Можна легко переконатися, що ряд збігається для будь-якого 

Зробивши аналогічні викладки, можна знайти розклад функції  в ряд:
в ряд:
 для
для  (8.48).
(8.48).
Розклад бінома Ньютона 
Нехай 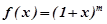 , де
, де  число ціле або дробове, додатне або від’ємне.
число ціле або дробове, додатне або від’ємне.
Тоді маємо: 
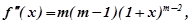

…….…………………………………………

………….……………………………………………………
Поклавши  у всіх цих формулах, одержимо:
у всіх цих формулах, одержимо:

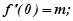


 .
.
Підставивши вирази для  в ряд Маклорена (8.45) будемо мати
в ряд Маклорена (8.45) будемо мати
 (8.49)
(8.49)
Користуючись формулою 
 , знайдемо інтервал збіжності
, знайдемо інтервал збіжності  ряду (8.49).
ряду (8.49).
Ми маємо:


Звідси  , і відповідно
, і відповідно
 (8.50)
(8.50)
Таким чином, біноміальний ряд збігається для 
 і розбігається зовні. Чи збігається цей ряд в точках
і розбігається зовні. Чи збігається цей ряд в точках  і
і  , необхідно досліджувати для кожного випадку окремо.
, необхідно досліджувати для кожного випадку окремо.
§10. Розклад функції в ряд Тейлора
В деяких випадках функція 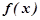 або її похідні втрачають зміст в точці
або її похідні втрачають зміст в точці  , як, наприклад
, як, наприклад  або
або  .
.
Такі функції не можуть бути розкладені в ряд Маклорена. Для розкладу такого роду функцій можна скористатись більш загальними степеневими рядами, розкладеними за степенями 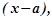 де
де  підібране, в конкретному випадку, постійне число.
підібране, в конкретному випадку, постійне число.
В розділі 4 було доведено, що якщо функція 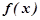 диференційована
диференційована  раз в інтервалі
раз в інтервалі  ,то має місце формула Тейлора:
,то має місце формула Тейлора:

 (8.51)
(8.51)
де  (
(  ) – залишковий член у формі Лагранжа. Число с можна записати у вигляді
) – залишковий член у формі Лагранжа. Число с можна записати у вигляді 
 , де
, де 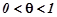 .
.
Якщо при необмеженому зростанні  , тобто при
, тобто при 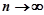 ,
,
 (8.52)
(8.52)
то із формули Тейлора одержимо розклад функції 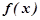 в ряд по степенях
в ряд по степенях  , який називається рядом Тейлора:
, який називається рядом Тейлора:
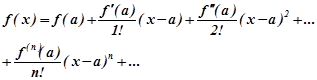 (8.53)
(8.53)
Умова (8.52) служить необхідною і достатньою умовою того, що ряд Тейлора для функції, яка необмежене число раз диференційована, збігається до цієї функції.
Приклад. Розкласти в ряд за степенями  функцію
функцію
 .
.
Розв’язування. Продиференціюємо функцію 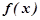 :
:  Підставивши
Підставивши  в попередні формули, одержимо:
в попередні формули, одержимо:  Використовуючи ряд Тейлора (8.53), одержимо такий розклад функції
Використовуючи ряд Тейлора (8.53), одержимо такий розклад функції 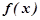 по степенях
по степенях  :
: 
Знаходимо радіус збіжності даного ряду:  . Тут
. Тут
 .
. 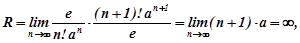 при будь-якому
при будь-якому 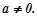
Отже, область збіжності ряду буде 
§11. Застосування степеневих рядів до
наближених обчислень
Одержані розклади деяких функцій в степеневі ряди в §10,11 дають можливість наближено обчислювати значення функції, визначені інтеграли, границі функції і т.д.
Приклад 1. Обчислити  , обмежившись двома членами розкладу.
, обмежившись двома членами розкладу.
Розв’язування. Використаємо формулу розкладу  в ряд за зростаючими степенями
в ряд за зростаючими степенями  :
:  .
.
Переведемо  в радіанну міру:
в радіанну міру: 
Тоді  . Підставивши замість
. Підставивши замість  одержимо
одержимо 
Приклад 2. Обчислити число  .
.
Розв’язування. Використаємо розклад функції  в ряд Маклорена:
в ряд Маклорена:
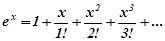 .
.
Поклавши  , одержимо
, одержимо  . Якщо за наближене значення числа
. Якщо за наближене значення числа  взяти суму перших семи членів цього ряду
взяти суму перших семи членів цього ряду  то одержимо
то одержимо 
Приклад 3. Обчислити  з точністю до 0,001.
з точністю до 0,001.
Розв’язування. Використаємо формулу біноміального ряду
 .
.
Якщо  ,
,  то одержимо
то одержимо

Оскільки в знакопереміжному ряді із спадними по абсолютній величині членами 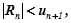 то похибка в наших обчисленнях не перевищує 0,0008, що забезпечує необхідну точність.
то похибка в наших обчисленнях не перевищує 0,0008, що забезпечує необхідну точність.
Приклад 4. Обчислити  обмежившись двома членами розкладу.
обмежившись двома членами розкладу.
Розв'язування. Запишемо число  у вигляді
у вигляді

У нашому випадку , поклавши в біноміальному ряді 
 матимемо
матимемо 
Приклад 5. Обчислити  , обмежившись трьома членами розкладу.
, обмежившись трьома членами розкладу.
Розв'язування. Число  представимо так:,
представимо так:,
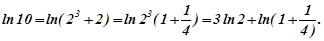 Поклавши у фор- мулі
Поклавши у фор- мулі  значення
значення 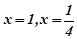 , одержимо
, одержимо
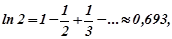

Тоді 
Приклад 6. Обчислити визначений інтеграл  обмежившись чотирма членами розкладу функції
обмежившись чотирма членами розкладу функції 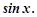
Розв’язування. Оскільки невизначений інтеграл  не може бути виражений в елементарних функціях і формулу Ньютона-Лейбніца не можна використати, даний інтеграл обчислимо наближено, використовуючи теорію рядів. Розділимо праву частину розкладу функції
не може бути виражений в елементарних функціях і формулу Ньютона-Лейбніца не можна використати, даний інтеграл обчислимо наближено, використовуючи теорію рядів. Розділимо праву частину розкладу функції  в ряд
в ряд
 на х і проінтегруємо одержаний вираз:
на х і проінтегруємо одержаний вираз: 
Приклад 7. Обчислити 
Розв’язування. Замінивши в рівності 
 на ”-
на ”-  ” і проінтегрувавши в межах від 0 до 0,3, одержимо
” і проінтегрувавши в межах від 0 до 0,3, одержимо 
Приклад 8. Знайти 
Розв’язування. Оскільки  ,
,
 то
то

Приклад 9. Знайти розв’язок диференціального рівняння
 (8.54)
(8.54)
який задовольняє початковим умовам
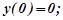
 . (8.55)
. (8.55)
Розв’язування. Шукаємо розв’язок  у вигляді ряду
у вигляді ряду
 (8.56)
(8.56)
Знайшовши похідну  і використавши (8.55), одержимо
і використавши (8.55), одержимо 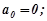
 Тоді
Тоді 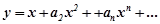
Продиференціювавши розклад  два рази, одержимо:
два рази, одержимо:

Підставивши  в (8.54) і замінивши
в (8.54) і замінивши  його розкладом (8.48), знаходимо:
його розкладом (8.48), знаходимо:

Прирівнявши коефіцієнти при однакових степенях  , одержимо:
, одержимо:


Звідси випливає, що 

 (8.57)
(8.57)
Підставивши постійні (8.57) в розклад (8.56) маємо:  , що відповідає розкладу функції
, що відповідає розкладу функції  по степенях
по степенях 
Перевірка. Підставимо 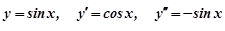 у рівняння (8.54):
у рівняння (8.54):
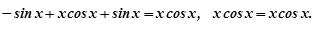
Розв’язок рівняння (8.54) знайдено правильно.