 |
|
Знакочередующиеся ряды. Исследование на сходимость
Определение. Знакочередующимся рядомназывается ряд вида
 ,
,
где  для всех
для всех 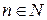 , т. е. ряд, в котором положительные и отрицательные члены чередуются.
, т. е. ряд, в котором положительные и отрицательные члены чередуются.
Для знакочередующихся рядов имеет место достаточный признак сходимости Лейбница.
Теорема (признак Лейбница). Знакочередующийся ряд  сходится, если выполняются следующие два условия:
сходится, если выполняются следующие два условия:
1. Последовательность абсолютных величин членов ряда  монотонно убывает, т. е.
монотонно убывает, т. е.  ;
;
2. Общий член ряда по абсолютной величине  стремится к нулю:
стремится к нулю:  .
.
При этом сумма ряда 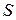 удовлетворяет неравенствам
удовлетворяет неравенствам 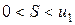 .
.
Если хотя бы одно из условий не выполняется, то знакочередующийся ряд расходится.
Замечание.Теорема Лейбница справедлива, если условие 1) выполняется, начиная только с некоторого номера  .
.
Замечание. Исследование на сходимость знакочередующегося ряда  , начинающегося с отрицательного числа, проводится также по признаку Лейбница.
, начинающегося с отрицательного числа, проводится также по признаку Лейбница.
Пример 14.1.Исследовать на сходимость ряд  .
.
□Решение. Применим признак Лейбница. Здесь  .
.
1.  ,
,  ,
,
 ,
,  ,….
,….
 – условие 1:
– условие 1:  не выполняется. Следовательно, второе условие проверять нет необходимости. Если хотя бы одно из условий не выполняется, то знакочередующийся ряд расходится.■
не выполняется. Следовательно, второе условие проверять нет необходимости. Если хотя бы одно из условий не выполняется, то знакочередующийся ряд расходится.■
Пример 14.2.Исследовать на сходимость ряд  .
.
□Решение. Применим признак Лейбница. Здесь  .
.
1.  ,
,  ,
,  ,…
,…
 – условие 1:
– условие 1:  выполняется.
выполняется.
2.  – условие 2:
– условие 2:  выполняется.
выполняется.
Следовательно, ряд сходится.■
14.2. Абсолютная и условная сходимость знакочередующихся рядов
Сходящийся знакочередующийся ряд  , где
, где  для всех
для всех 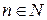 имеет два вида сходимости: абсолютную и условную.
имеет два вида сходимости: абсолютную и условную.
Определение.Знакочередующийся ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.
Определение.Знакочередующийся ряд называется условно сходящимся, если ряд, составленный из модулей его членов, расходится.
Если знакочередующийся ряд имеет вид  , то ряд, составленный из модулей его членов
, то ряд, составленный из модулей его членов 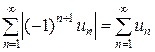 – числовой ряд с положительными членами.
– числовой ряд с положительными членами.
Свойство.Если знакочередующийся ряд сходится абсолютно и имеет сумму 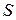 , то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму
, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму 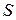 , что и исходный.
, что и исходный.
Свойство.Переставляя члены условно сходящегося ряда, можно добиться того, что сумма ряда изменится или получится вообще расходящийся ряд.
Пример 14.3.Исследовать на сходимость ряд  .
.
□Решение. Применим признак Лейбница. Здесь  .
.
1.  ,
,  ,
,  ,
,  ,….
,….
 – условие 1:
– условие 1:  выполняется.
выполняется.
2.  – условие 2:
– условие 2:  выполняется.
выполняется.
Следовательно, ряд сходится. Выясним характер сходимости, т. е. как сходится: условно или абсолютно. Для этого составим ряд из модулей его членов.
 – числовой ряд с положительными членами, являющийся обобщенным гармоническим рядом вида
– числовой ряд с положительными членами, являющийся обобщенным гармоническим рядом вида 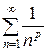 . Известно, что он сходится при
. Известно, что он сходится при 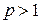 и расходится при
и расходится при 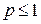 . Здесь
. Здесь  ,следовательно, ряд
,следовательно, ряд 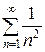 сходится. В итоге, исходный знакочередующийся ряд
сходится. В итоге, исходный знакочередующийся ряд  сходится абсолютно.■
сходится абсолютно.■
Пример 14.4.Исследовать на сходимость ряд  .
.
□Решение. Применим признак Лейбница. Здесь  .
.
1. 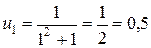 ,
,  ,
,
 ,
, 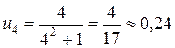 ,…
,…
 – условие 1:
– условие 1:  выполняется.
выполняется.
2. 
 – условие 2:
– условие 2:  выполняется.
выполняется.
Следовательно, ряд сходится. Выясним характер сходимости, т. е. как сходится: условно или абсолютно. Для этого составим ряд из модулей его членов.
 – числовой ряд с положительными членами,
– числовой ряд с положительными членами,
Применим второй признак сравнения.Сравним данный ряд с “эталонным” – гармоническим рядом 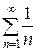 , который расходится. Вычислим предел
, который расходится. Вычислим предел

Так как предел конечен и отличен от нуля, то ряд 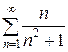 тоже расходится, следовательно, исходный ряд
тоже расходится, следовательно, исходный ряд  сходится условно.■
сходится условно.■