 |
|
Сходимость степенных рядов
Область сходимости степенного ряда (15.2) содержит, по крайней мере, одну точку: 
. Так как в этом случае ряд будет иметь вид 
, т. е. сумма ряда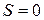 
– конечное число. А это означает, что ряд сходится.
Аналогично, область сходимости степенного ряда (15.3) содержит, по крайней мере, одну точку: 
.
Теорема Абеля(основное свойство степенных рядов).Если степенной ряд (15.2)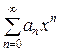 
сходится при 
, то он сходится (и притом абсолютно, т. е. ряд из модулей тоже сходится) при любом значении 
, удовлетворяющем неравенству 
, 
(или при 
).
Определение. Областью сходимости степенного ряданазывается множество значений переменной , при которых ряд сходится.
Область сходимости степенного ряда (15.2) 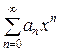определяется из условия
, где число 
называется радиусом сходимости. Внутри интервала или 
ряд (15.2) сходится абсолютно, вне интервала – расходится. Для определения сходимости ряда на концах интервала , т. е. в точках 
требуется дополнительное исследование, т. к. ряд может вести себя по-разному.
Замечание.Если 
, то степенной ряд (15.2) сходится абсолютно лишь при , и интервал сходимости не существует.
Замечание.Если 
, то степенной ряд (15.2) сходится абсолютно на всей числовой оси, т. е. при любом 
.
Область сходимости степенного ряда (15.3) 
определяется из условия
. Внутри интервала или 
, ряд (15.3) сходится абсолютно, вне интервала – расходится. Для определения сходимости ряда на концах интервала , т. е. в точках 
требуется дополнительное исследование, т. к. ряд (15.3), так же как и ряд (15.2), на концах интервала может вести себя по-разному.
Для определения интервала и радиуса сходимости степенных рядов (15.2) 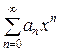и (15.3) можно пользоваться одним из следующих способов.
1 способ.Если среди коэффициентов 
нет равных нулю, т. е. ряд содержит все целые положительные степени для ряда (15.2) 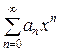или 
для ряда (15.3) , то 
при условии, что этот предел (конечный или бесконечный) существует.
2 способ.Если среди коэффициентов нет равных нулю, т. е. ряд содержит все целые положительные степени для ряда (15.2) 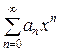или для ряда (15.3) , то 
при условии, что этот предел (конечный или бесконечный) существует.
3 способ.Во всех случаях интервал сходимости можно находить, применяя непосредственно признак Даламбера или радикальный признак Коши к ряду, составленному из абсолютных величин членов ряда. Так, если степенной ряд имеет вид
,
то интервал сходимости можно определить из неравенства 
или 
.
Пример 15.1.Найти область сходимости ряда 
.
□Решение. Здесь 
, 
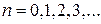Среди коэффициентов нет равных нулю, поэтому область сходимости можно найти путем нахождения радиуса сходимости 1-м или 2-м способом. С учетом вида коэффициента рациональней применить формулу .
Так как , то 
. Определим радиус сходимости:
.
Следовательно, и интервал сходимости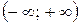 
, т. е. данный ряд сходится абсолютно на всей числовой оси.■
Пример 15.2. Найти область сходимости ряда 
.
□Решение. Здесь 
, 
Среди коэффициентов нет равных нулю, поэтому область сходимости можно найти путем нахождения радиуса сходимости 1-м или 2-м способом. С учетом вида коэффициента рациональней применить формулу .
Так как , то 
. Определим радиус сходимости:
.
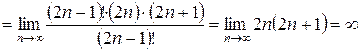Следовательно, и интервал сходимости 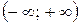, т. е. данный ряд сходится абсолютно на всей числовой оси.■
Пример 15.3.Найти область сходимости ряда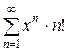 
.
□Решение. Здесь 
, Среди коэффициентов нет равных нулю, поэтому область сходимости можно найти путем нахождения радиуса сходимости 1-м или 2-м способом. С учетом вида коэффициента рациональней применить формулу .
Так как , то 
. Определим радиус сходимости:
.
Следовательно, и ряд сходится абсолютно в единственной точке 
.■
Пример 15.4. Найти область сходимости ряда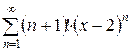 
.
□Решение. Здесь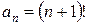 
, Среди коэффициентов нет равных нулю, поэтому область сходимости можно найти путем нахождения радиуса сходимости 1-м или 2-м способом. С учетом вида коэффициента 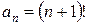рациональней применить формулу .
Так как 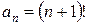, то 
. Определим радиус сходимости:
.
Следовательно, и ряд сходится абсолютно в единственной точке 
.■
Пример 15.5.Найти область сходимости ряда 
.
□Решение. Здесь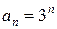 
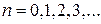, Среди коэффициентов нет равных нулю, поэтому область сходимости можно найти путем нахождения радиуса сходимости 1-м или 2-м способом. С учетом вида коэффициента 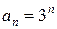рациональней применить формулу .
Определим радиус сходимости:
.
Следовательно, 
и ряд сходится абсолютно при 
.
Исследуем сходимость ряда на концах интервала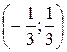 
, т. е. в точках 
.
а) Подставим 
в исходный ряд . Получим
.
Очевидно, что сумма ряда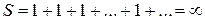 
, т. е. ряд расходится, и, следовательно, исходный степенной ряд при расходится.
б) Подставим 
в исходный ряд . Получим
– знакочередующийся числовой ряд.
Исследуем его на сходимость с помощью признака Лейбница. Здесь 
, поэтому оба условия в признаке Лейбница не выполняются, и, следовательно, ряд расходится. Таким образом, исходный степенной ряд при тоже расходится
В итоге ряд сходится при .■
Пример 15.6.Найти область сходимости ряда 
.
□Решение. Здесь 
, Среди коэффициентов нет равных нулю, поэтому область сходимости можно найти путем нахождения радиуса сходимости 1-м или 2-м способом. С учетом вида коэффициента рациональней применить формулу .
Так как , то 
. Определим радиус сходимости:
.
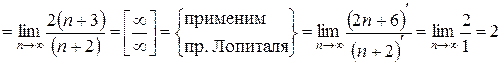Следовательно, 
и ряд сходится абсолютно при 
.
Исследуем сходимость ряда на концах интервала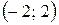 
, т. е. в точках 
.
а) Подставим в исходный ряд . Получим
– числовой ряд с положительными членами.
Исследуем его на сходимость. Для этого применим второй признак сравнения.Сравним данный ряд с “эталонным” рядом – гармоническим рядом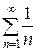 
, который расходится. Вычислим предел
.
Так как предел конечен и отличен от нуля, то ряд 
тоже расходится, т. е. исходный степенной ряд при расходится.
б) Подставим 
в исходный ряд . Получим
– знакочередующийся числовой ряд.
Исследуем его на сходимость. Для этого применим признак Лейбница. Здесь 
.
1. 
, 
, 
, 
,…
– условие 1: 
выполняется.
2. 
– условие 2: 
выполняется.
Следовательно, ряд 
сходится. Выясним характер сходимости, т. е. как сходится: условно или абсолютно. Для этого составим ряд из модулей его членов.
– числовой ряд с положительными членами.
В пункте а) мы показали, что он расходится. Это означает, что ряд сходится условно, т. е. исходный степенной ряд при сходится, но условно.
Таким образом, ряд сходится при 
, причем при сходимость условная.■
Пример 15.7. Найти область сходимости ряда 
.
□Решение. Здесь 
, Среди коэффициентов нет равных нулю, поэтому область сходимости можно найти путем нахождения радиуса сходимости 1-м или 2-м способом. С учетом вида коэффициента рациональней применить формулу .
Так как , то 
. Определим радиус сходимости:
.
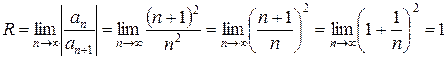Следовательно,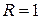 
и ряд сходится абсолютно при 
.
Исследуем сходимость ряда на концах интервала 
, т. е. в точках 
.
а) Подставим 
в исходный ряд . Получим
– числовой ряд с отрицательными членами.
Составим ряд из модулей его членов:
– числовой ряд с положительными членами, являющийся обобщенным гармоническим рядом вида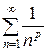 
. Известно, что он сходится при 
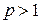. Следовательно, ряд 
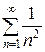сходится, и ряд с отрицательными членами 
сходится абсолютно. Это означает, что исходный степенной ряд при сходится абсолютно.
б) Подставим 
в исходный ряд . Получим
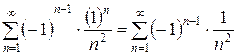– знакочередующийся числовой ряд.
Исследуем его на сходимость. Для этого применим признак Лейбница. Здесь 
.
1. 
, 
, 
, 
,…
– условие 1: выполняется.
2. 
– условие 2: выполняется.
Следовательно, ряд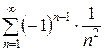 
сходится. Выясним характер сходимости, т. е. как сходится: условно или абсолютно. Для этого составим ряд из модулей его членов.
– числовой ряд с положительными членами, являющийся сходящимся обобщенным гармоническим рядом (пункт а). В итоге, исходный знакочередующийся ряд 
сходится абсолютно, т. е. исходный степенной ряд при 
сходится абсолютно.
Таким образом, ряд сходится при 
, причем при 
сходимость абсолютная.■
Пример 15.8. Найти область сходимости ряда 
.
□Решение. Здесь 
, Среди коэффициентов нет равных нулю, но сам ряд не имеет вид 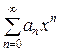, поэтому воспользуемся универсальным способом 3. С учетом вида общего члена ряда 
рациональней использовать неравенство .
Так как , то 
. Вычислим отношение 
и его предел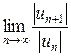 
:
.
.
Определим, при каких значениях предел 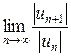будет меньше единицы. Для этого решим неравенство 
:
.
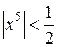
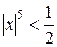
Следовательно, исходный ряд сходится абсолютно при 
. Исследуем сходимость ряда на концах интервала 
, т. е. в точках 
.
а) Подставим 
в исходный ряд . Получим
– числовой ряд с положительными членами.
Исследуем его на сходимость. Для этого применим второй признак сравнения.Сравним данный ряд с “эталонным” рядом – гармоническим рядом 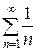, который расходится. Вычислим предел
.
Так как предел конечен и отличен от нуля, то ряд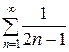 
тоже расходится, т. е. исходный степенной ряд при расходится.
б) Подставим 
в исходный ряд . Получим
– знакочередующийся числовой ряд.
Исследуем его на сходимость. Для этого применим признак Лейбница. Здесь 
.
1. 
, 
, 
, 
,…
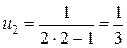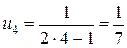– условие 1: выполняется.
2. 
– условие 2: выполняется.
Следовательно, ряд 
сходится. Выясним характер сходимости, т. е. как сходится: условно или абсолютно. Для этого составим ряд из модулей его членов.
– числовой ряд с положительными членами.
В пункте а) мы показали, что он расходится. Это означает, что ряд сходится условно, т. е. исходный степенной ряд при сходится, но условно.
Таким образом, ряд сходится при 
, причем при сходимость условная.■