 |
|
Интегрирование четных и нечетных функций в симметричных пределах
Определение. Функция  , определенная на множестве
, определенная на множестве  , называется четной, если для любого
, называется четной, если для любого  выполняются условия
выполняются условия  и
и  ;нечетной, если для любого
;нечетной, если для любого  выполняются условия
выполняются условия  и
и  .
.
Например:
функция  – четная, т. к.
– четная, т. к.  ;
;
функция  – нечетная, т. к.
– нечетная, т. к.  .
.
График четной функции симметричен относительно оси  , а нечетной – относительно начала координат.
, а нечетной – относительно начала координат.
Пример 17.1. Установить четность или нечетность функций:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  .
.
□Решение. В рассматриваемых примерах область каждой из функций симметрична относительно нуля:  .
.
1) Заменяя  на
на  , получим
, получим
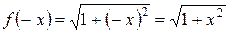 ,
,
т. е.  . Значит, данная функция является четной.
. Значит, данная функция является четной.
2) Заменяя  на
на  , получим
, получим
 ,
,
т. е.  и
и  . Значит, данная функция не является ни четной, ни нечетной.
. Значит, данная функция не является ни четной, ни нечетной.
3) Заменяя  на
на  , получим
, получим
 ,
,
т. е.  . Значит, данная функция является четной.
. Значит, данная функция является четной.
4) Заменяя  на
на  , получим
, получим
 ,
,
т. е.  . Значит, данная функция является нечетной.
. Значит, данная функция является нечетной.
5) Заменяя  на
на  , получим
, получим
 ,
,
т. е.  . Значит, данная функция является четной.
. Значит, данная функция является четной.
6) Заменяя  на
на  , получим
, получим
 ,
,
т. е.  . Значит, данная функция является нечетной.■
. Значит, данная функция является нечетной.■
Интегрирование четных и нечетных функций на отрезке  , симметричном относительно точки
, симметричном относительно точки  , упрощается при использовании следующих свойств:
, упрощается при использовании следующих свойств:
Если  – нечетная функция, то
– нечетная функция, то  . (17.1)
. (17.1)
Если  – четная функция, то
– четная функция, то  . (17.2)
. (17.2)
Благодаря свойствам (17.1) и (17.2) можно, например, сразу, не производя вычислений, сказать, что
 ,
,  ,
,  .
.
17.2. Разложение в ряд Фурье  -периодических функций
-периодических функций
Определение.Функция 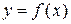 , определенная на множестве
, определенная на множестве  , называется периодической с периодом
, называется периодической с периодом  , если при каждом
, если при каждом  значение
значение  и выполняется равенство
и выполняется равенство  .
.
Если  – период функции, то ее периодами будут также числа
– период функции, то ее периодами будут также числа  , где
, где  Так, для функций
Так, для функций  и
и  периодами будут числа
периодами будут числа  Основной период (наименьший положительный) – это период
Основной период (наименьший положительный) – это период  .
.
Для построения графика периодической функции периода  достаточно построить его на любом отрезке длины
достаточно построить его на любом отрезке длины  и периодически продолжить его во всю область определения.
и периодически продолжить его во всю область определения.
Определение. Рядом Фурье (тригонометрическим рядом) периодической функции  с периодом
с периодом  , определённой на сегменте
, определённой на сегменте  , называется ряд вида
, называется ряд вида
 , (17.3)
, (17.3)
где действительные числа  ,
,  ,
, 
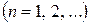 называются коэффициентами ряда Фурье.
называются коэффициентами ряда Фурье.
Коэффициенты ряда (17.3) определяются по формулам

 ,
,  ,
,  . (17.4)
. (17.4)
Пример 17.2.Разложить в ряд Фурье на промежутке  периодическую с периодом
периодическую с периодом  функцию
функцию  .
.
□Решение. Проверим функцию на четность, нечетность. Заменяя  на
на  , получим
, получим
 ,
,
т. е.  и
и  . Значит, данная функция не является ни четной, ни нечетной.
. Значит, данная функция не является ни четной, ни нечетной.
Найдем коэффициенты  ,
,  , и
, и  по формулам (17.4):
по формулам (17.4):

 ;
;


 ;
;




 .
.
Следовательно, на промежутке  исходной функции
исходной функции  соответствует ряд Фурье(17.3) вида
соответствует ряд Фурье(17.3) вида  .■
.■
17.3. Разложение в ряд Фурье четных и нечетных функций на отрезке 
Если разлагаемая на отрезке  в ряд Фурье функция
в ряд Фурье функция  является четной или нечетной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится неполным).
является четной или нечетной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится неполным).
Если периодическая функция  с периодом
с периодом  , определённая на отрезке
, определённая на отрезке  , является четной, то ее ряд Фурье имеет вид
, является четной, то ее ряд Фурье имеет вид
 , (17.5)
, (17.5)
где коэффициенты  и
и  (
(  ) определяются по формулам
) определяются по формулам
 ,
,  ,
, 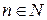 . (17.6)
. (17.6)
Если периодическая функция  с периодом
с периодом  , определенная на сегменте
, определенная на сегменте  , является нечетной, то ее ряд Фурье имеет вид
, является нечетной, то ее ряд Фурье имеет вид
 , (17.7)
, (17.7)
где коэффициент  (
(  ,
,  ) определяется по формуле
) определяется по формуле
 . (17.8).
. (17.8).
Пример 17.3.Разложить в ряд Фурье на промежутке  периодическую с периодом
периодическую с периодом  функцию
функцию  .
.
□Решение. Проверим функцию на четность, нечетность. Заменяя  на
на  , получим
, получим
 ,
,
т. е.  . Значит, данная функция является четной. Следовательно,
. Значит, данная функция является четной. Следовательно,  ,
, 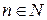 .
.
Найдем коэффициенты  и
и  по формулам (17.6):
по формулам (17.6):
 ;
;


 .
.
Следовательно, на промежутке  исходной функции
исходной функции 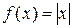 соответствует ряд Фурье(17.5)
соответствует ряд Фурье(17.5)  .■
.■
Пример 17.4.Разложить в ряд Фурье на промежутке  периодическую с периодом
периодическую с периодом  функцию
функцию  .
.
□Решение: Проверим функцию на четность, нечетность. Заменяя  на
на  , получим
, получим
 ,
,
т. е.  . Значит, данная функция является нечетной. Следовательно,
. Значит, данная функция является нечетной. Следовательно,  ,
,  ,
, 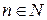 .
.
Найдем коэффициент  по формуле (17.8):
по формуле (17.8):


 .
.
Следовательно, на промежутке  исходной функции
исходной функции  соответствует ряд Фурье (17.7)
соответствует ряд Фурье (17.7)  .■
.■
17.4. Разложение в ряд Фурье функций произвольного периода 
Определение. Рядом Фурье периодической функции  с периодом
с периодом  , определённой на сегменте
, определённой на сегменте 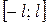 называется ряд вида
называется ряд вида
 , (17.9)
, (17.9)
где действительные числа  ,
,  ,
, 
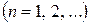 называются коэффициентами ряда Фурье.
называются коэффициентами ряда Фурье.
Коэффициенты ряда (17.9) определяются по формулам
 . (17.10)
. (17.10)
Пример 17.5. Разложить в ряд Фурье периодическую функцию  заданную на интервале-периоде
заданную на интервале-периоде 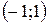 .
.
□Решение.
Поскольку функция  является кусочно-заданной, то для проверки ее на четность, нечетность лучше воспользоваться графиком этой функции (см. рис. 17.1). По чертежу видно, что для произвольной точки является кусочно-заданной, то для проверки ее на четность, нечетность лучше воспользоваться графиком этой функции (см. рис. 17.1). По чертежу видно, что для произвольной точки   и и  . Значит, данная функция не является ни четной, ни нечетной. . Значит, данная функция не является ни четной, ни нечетной.
|  Рис. 17.1
Рис. 17.1
|
Из условия задачи следует, что т. к.  , то период
, то период  . Вычислим все коэффициенты ряда Фурье
. Вычислим все коэффициенты ряда Фурье  ,
,  , и
, и  по формулам (17.10):
по формулам (17.10):
 ;
;



 ;
;



 .
.
Следовательно, на промежутке  исходной функции соответствует ряд Фурье (17.9)
исходной функции соответствует ряд Фурье (17.9)  .■
.■
17.5. Разложение в ряд Фурье четных и нечетных функций на отрезке 
Если периодическая функция  с периодом
с периодом  , определённая на отрезке
, определённая на отрезке  , является четной, то ее ряд Фурье имеет вид
, является четной, то ее ряд Фурье имеет вид
 , (17.11)
, (17.11)
где коэффициенты  и
и  (
(  ) определяются по формулам
) определяются по формулам
 ,
,  ,
, 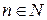 . (17.12)
. (17.12)
Если периодическая функция  с периодом
с периодом  , определенная на сегменте
, определенная на сегменте  , является нечетной, то ее ряд Фурье имеет вид
, является нечетной, то ее ряд Фурье имеет вид
 , (17.13)
, (17.13)
где коэффициент  (
(  ,
,  ) определяется по формуле
) определяется по формуле
 . (17.14).
. (17.14).