 |
|
Абсолютная и условная сходимость числовых рядов.
Свойства абсолютно сходящихся рядов.
Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.
Знакопеременный ряд называется условно сходящимся, если сам сходится, а ряд, составленный из модулей его членов, расходится.
Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место: на такие ряды переносятся основные свойства конечных сумм:
- Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд (теорема Дирихле)
- Абсолютно сходящиеся ряды с суммами
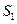и 
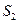можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна 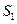+ 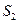(или соответственно 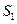- 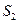) - Под произведением двух рядов
и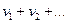 
понимают ряд вида
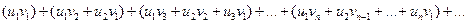
Произведение двух абсолютно сходящихся рядов с суммам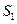и и 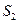есть абсолютно сходящийся ряд, сумма которого равна .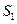
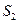Степенные ряды
Функциональные ряды
Основные понятия
Ряд, членами которого являются функции от х, называется функциональным:
Придавая х определенное значение 
, мы получим числовой ряд
,
который может быть как сходящимся, так и расходящимся.
Если полученный числовой ряд сходится, то точка называется точкой сходимости ряда ; если же ряд расходится – точкой расходимости функционального ряда.
Совокупность числовых значений аргумента х, при которых функциональный ряд сходится, называются его областью сходимости.
В области сходимости функционального ряда его сумма является некоторой функцией от х: S=S(x). Определяется она в области сходимости равенством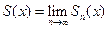 
,где 
– частичная сумма ряда.
Среди функциональных рядов особую роль играет ряд, членами которого являются степенные функции аргумента х, т.е. так называемый степенной ряд:
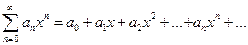
Действительные (или комплексные) числа 
называются коэффициентами ряда, 
- действительная переменная.
Ряд 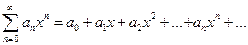расположен по степеням х. Рассматривают также степенной ряд, расположенный по степеням 
, т.е. ряд вида 
, где – некоторое постоянное число.
Сходимость степенных рядов.
Область сходимости степенного ряда содержит по крайней мере одну точку: х=0 (ряд сходится в точке)
Теорема Н. Абеля
Теорема
Если степенной ряд 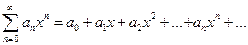сходится при 
, то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству 
По условию ряд 
сходится. Следовательно, по необходимому признаку сходимости 
. Отсюда следует, что величина 
ограничена, т.е. найдется такое число М>0, что для всех n выполняется неравенство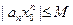 
, n=1, 2,..
Пусть , тогда величина 
и, следовательно, 
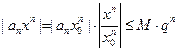, т.е. модуль каждого члена ряда 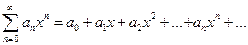не превосходит соответствующего члена сходящегося (q<1) ряда геометрической прогрессии. Поэтому по признаку сравнения при ряд 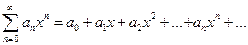абсолютно сходящийся.
Следствие
Если ряд 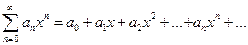расходится при 
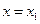, то он расходится и при всех х, удовлетворяющих неравенству 
Действительно, если допустить сходимость ряда в точке 
, для которой 
, то по теореме Абеля ряд сходится при всех х, для которых 
, и, в частности, в точке 
, что противоречит условию.