Главная | Обратная связь

Простейшие свойства сходящихся рядов.

Министерство образования и науки Украины

ЮЖНЫЙ ФИЛИАЛ «КРЫМСКИЙ АГРОТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ» НАЦИОНАЛЬНОГО АГРАРНОГО УНИВЕРСИТЕТА

 

Кафедра физики и математики

 

Е.И. Степанова

 

 

КОНСПЕКТ ЛЕКЦИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ

 

Часть 3

 

Симферополь – 2007 г.

Лекция 1.

Числовые ряды. Сходимость и сумма ряда. Примеры. Простейшие свойства сходящихся рядов. Необходимое условие сходимости. Остаток ряда. Ряды с неотрицательными членами, критерий сходимости.

Определение 1.1. Бесконечная сумма чисел

u₁ + u₂ +…+ u_n +… (или ), (1.1)

где каждое число и_п можно вычислить, зная его номер п, называется числовым рядом.

При этом формула u_n = f(n), позволяющая найти каждый член ряда, называется формулой общего членаряда.

 

Определение 1.2. Сумма конечного числа п первых членов ряда называется частичной суммой ряда:

s_n = u₁ + u₂ +…+ u_n (1.2)

 

Определение 1.3. Если существует конечный предел частичных сумм ряда:

, (1.3)

то говорят, что ряд сходится, а число s называется суммой ряда. Если конечный 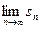не существует, то ряд (1.1) называется расходящимся.

 

Замечание. Таким образом, свойства числовых рядов во многом определяются свойствами числовых последовательностей {s_n}.

 

Пример 1. Ряд сходится, так как представляет собой бесконечно убывающую геометрическую прогрессию со знаменателем 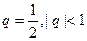, сумму которой можно найти по формуле .

Пример 2. Рассмотрим ряд 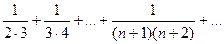. Представим общий член ряда в виде: . Тогда частичная сумма s_n будет выглядеть так:

. Тогда . Следовательно, ряд сходится, и его сумма равна .

Пример 3. Ряд 1+1+1+…+1+… расходится, так как

 

Пример 4. Ряд 1-1+1-1+…+(-1)^п+1+… тоже расходится, так как последовательность его частичных сумм имеет вид: s₁ = 1, s₂ = 0, s₃ = 1, s₄ = 0 и т.д., а такая последовательность предела не имеет.

 

Простейшие свойства сходящихся рядов.

Теорема 1.1. Исключение или добавление конечного числа слагаемых не влияет на сходимость ряда.

Доказательство.

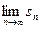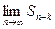Исключим из ряда (1.1) произвольные k членов и выберем значение п, при котором все отброшенные члены содержатся в частичной сумме s_n. Тогда s_n = c_k + S_n-k , где c_k – сумма отброшенных членов ряда, а S_n-k – сумма членов, входящих в s_n, но не входящих в c_k . Тогда , так как c_k – постоянная величина, не зависящая от п. Следовательно, конечные пределы и существуют или не существуют одновременно, что и доказывает утверждение теоремы.

 

Теорема 1.2. Если сходится ряд u₁ + u₂ +…+ u_n +… и его сумма равна s, то сходится и ряд cu₁ + cu₂ +…+ cu_n +…, сумма которого равна cs.

Доказательство. Обозначим частичную сумму второго ряда c_n . Тогда

, что и требовалось доказать.

 

Теорема 1.3. Если ряды а₁ + а₂ +…+ а_п +… (1.4)

и b₁ + b₂ +…+ b_n +… (1.5)

сходятся и их суммы соответственно равны s_a и s_b, то ряды (a₁ + b₁) + (a₂ + b₂) +… (1.6)

и (a₁ – b₁) + (a₂ – b₂) +… (1.7)

тоже сходятся, и их суммы равны s_a + s_b и s_a – s_b .

Доказательство. Пусть σ_n – частичная сумма ряда (1.6), а (s_a)_n и (s_b)_n – частичные суммы из того же числа слагаемых рядов (1.4) и (1.5). Тогда σ_n = (s_a)_n + (s_b)_n, поэтому

. Следовательно, ряд (1.6) сходится, и его сумма равна

s_a + s_b . Аналогичным образом доказывается сходимость ряда (1.7).