Главная | Обратная связь

Знакопеременные ряды. Абсолютная и условная сходимости. Признак Лейбница. Свойства абсолютно сходящихся рядов.

Для числовых рядов, члены которых имеют разные знаки, задаются два вида сходимости.

 

Определение 3.1. Ряд называется абсолютно сходящимся, если сходится ряд из его модулей, то есть ряд .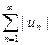

Теорема 3.1.. Если ряд абсолютно сходится, то он сходится и в обычном смысле, то есть существует конечный предел его частичных сумм.

Доказательство.

Пусть s_n = u₁ + u₂ +…+ u_n , s`_n – сумма всех положительных членов среди первых п членов данного ряда, s``_n – сумма модулей всех отрицательных членов среди них. Если обозначить σ_n = |u₁| + |u₂| +…+ |u_n|, то

s_n = s`<sub>n</sub> – s``<sub>n</sub> , σ<sub>n</sub> = s`_n + s``_n .

Так как по условию теоремы σ_п имеет предел σ, а s`<sub>n</sub> и s``<sub>n</sub> – положительные возрастающие величины, меньшие σ, то они тоже имеют пределы s` и s``. Следовательно,

,

то есть знакопеременный ряд сходится.

 

Замечание. Так как ряд 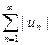является знакоположительным, то для исследования знакопеременного ряда на абсолютную сходимость мы можем использовать все известные признаки сходимости знакоположительных рядов.

 

Пример. Для ряда ряд из модулей имеет вид . Такой ряд сходится (см. пример из лекции 1), поэтому рассматриваемый ряд сходится абсолютно.

 

Определение 3.2. Если ряд, составленный из модулей членов данного ряда, расходится, а сам данный ряд сходится, то говорят, что он сходится условно.

 

Признак Лейбница.

Если знакопеременный ряд не обладает абсолютной сходимостью, то требуется ответить на вопрос, будет ли он сходиться хотя бы условно. Ответ на него можно дать, применяя признак Лейбница:

 

Теорема 3.2. Если исследуемый ряд:

1) знакочередующийся, то есть имеет вид u₁ – u₂ + u₃ – u₄ +… , где u_i > 0; (3.1)

2) u₁ > u₂ > u₃ >… > u_n > u_n+1 >… (последующий член ряда по модулю меньше предыдущего);

3)

то ряд сходится (хотя бы условно), его сумма положительна и .

 

Доказательство. Рассмотрим первых 2т членов ряда:

s_2m = (u₁ – u₂) + (u₃ – u₄) +…+ (u_2m-1 – u_2m) > 0,

так как u_2i-1 – u_2i > 0. Итак, последовательность {s_2m} положительна и возрастает с возрастанием т. С другой стороны, s_2m можно записать в ином виде:

s_2m = u₁ – (u₂ – u₃) – (u₄ – u₅) -…- (u_2m-2 – u_2m-1) – u_2m < u₁ .

Следовательно, последовательность {s_2m} ограничена сверху и поэтому имеет предел:

Докажем, что тот же предел имеет и последовательность частичных сумм, составленных их нечетного числа слагаемых:

Таким образом, 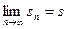при любом п, то есть ряд (3.1) сходится.

 

Пример. Исследуем на абсолютную и условную сходимость ряд .

|u_n| = (так как ln n < n), поэтому по первому признаку сравнения ряд 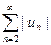расходится, то есть абсолютной сходимостью рассматриваемый ряд не обладает.

Проверим для него выполнение условий теоремы 3.2. Знакочередование обеспечивается множителем (-1)^п, а из монотонного возрастания функции

y = ln x следует, что ln(n + 1) > ln n, a . Следовательно, по признаку Лейбница ряд сходится условно.