Главная | Обратная связь

Свойства степенных рядов.

Теорема 5.2 (2-я теорема Абеля). Если R – радиус сходимости ряда (5.2) и этот ряд сходится при x = R, то он равномерно сходится на интервале (-R, R).

Доказательство.

знакоположительный ряд 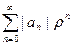сходится по теореме 5.1. Следова-тельно, ряд (5.2) равномерно сходится в интервале [-ρ, ρ] по теореме 4.1. Из выбора ρ следует, что интервал равномерной сходимости – (- R, R), что и требовалось доказать.

 

Следствие 1. На всяком отрезке, целиком лежащем внутри интервала сходимости, сумма ряда (5.2) есть непрерывная функция.

Доказательство.

Члены ряда (5.2) являются непрерывными функциями, и ряд равномерно сходится на рассматриваемом отрезке. Тогда непрерывность его суммы следует из теоремы 4.2.

 

Следствие 2. Если пределы интегрирования α, β лежат внутри интервала сходимости степенного ряда, то интеграл от суммы ряда равен сумме интегралов от членов ряда:

(5.5)

Доказательство этого утверждения следует из теоремы 4.3.

 

Теорема 5.3. Если ряд (5.2) имеет интервал сходимости (-R, R ), то ряд

φ(x) = a₁ + 2a₂x + 3a₃x² +…+ na_nx^n-1 +…, (5.6)

полученный почленным дифференцированием ряда (5.2), имеет тот же интервал сходимости (-R, R). При этом

φ΄(х) = s΄(x) при |x| < R , (5.7)

то есть внутри интервала сходимости производная от суммы степенного ряда равна сумме ряда, полученного его почленным дифференцированием.

Доказательство.

Выберем ρ: 0 < ρ < R и ζ: ρ < ζ < R. Тогда ряд 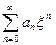сходится, следовательно, то есть Если |x| ≤ ρ, то

где Таким образом, члены ряда (5.6) по модулю меньше членов знакоположительного ряда , который сходится по признаку Даламбера:

то есть является мажорантой для ряда (5.6) при Поэтому ряд (5.6) равно-мерно сходится на [-ρ, ρ]. Следовательно, по теореме 4.4 верно равенство (5.7). Из выбора ρ следует, что ряд (5.6) сходится в любой внутренней точке интервала (-R, R).

Докажем, что вне этого интервала ряд (5.6) расходится. Действительно, если бы он сходился при x₁ > R, то, интегрируя его почленно на интервале (0, x₂), R < x₂ < x₁ , мы получили бы, что ряд (5.2) сходится в точке х₂ , что противоречит условию теоремы. Итак, теорема полностью доказана.

 

Замечание. Ряд (5.6) можно, в свою очередь, почленно дифференцировать и проделы-вать эту операцию сколько угодно раз.

Вывод: если степенной ряд сходится на интервале (-R, R), то его сумма представляет собой функцию, имеющую внутри интервала сходимости производные любого порядка, каждая из которых есть сумма ряда, полученного из исходного с помощью почленного дифференцирования соответствующее количество раз; при этом интервал сходимости для ряда из производных любого порядка есть (-R, R).

 

 

Лекция 6.