 |
|
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Уравнение гармонических колебаний точки вдоль оси Ox: 
,
где 
- амплитуда колебаний, 
- циклическая (круговая) частота, 
- начальная фаза колебаний в момент времени 
=0, 
- фаза колебаний в момент времени .
Циклическая частота колебаний: 
,
где 
- линейная частота колебаний, 
- период колебаний.
Скорость точки, совершающей гармонические колебания вдоль оси Ox : 
.
Ускорение точки, совершающей гармонические колебания вдоль оси Ox : 
.
Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний с одинаковыми частотами, происходящих по одной прямой
и 
,
определяется по формуле
,
где 
, 
и 
, 
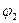- амплитуды и начальные фазы складываемых колебаний.
Начальная фаза 
результирующего гармонического колебания определяется по формуле:
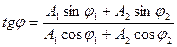
Уравнение траектории точки, участвующей в двух взаимно перпендикулярных гармонических колебаниях с амплитудами и , и начальными фазами и :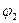
.
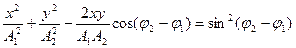Если начальные фазы и 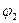складываемых колебаний одинаковы, то уравнение траектории принимает вид
.
Дифференциальное уравнение гармонических колебаний материальной точки, на которую действует упругая сила Fупр =-kx :
или 
,
где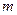 
- масса материальной точки, 
- коэффициент упругости, 
- циклическая частота свободных незатухающих колебаний.
Кинетическая энергия материальной точки, совершающей гармонические колебания:
.
Потенциальная энергия материальной точки, совершающей гармонические колебания:
.
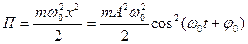Полная энергия материальной точки, совершающей гармонические колебания:
.
Период колебаний пружинного маятника: 
,
где 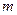- масса маятника, - коэффициент упругости пружины.
Период колебаний математического маятника: 
,
где 
- длина маятника, 
- ускорение свободного падения.
Период колебаний физического маятника: 
,
где 
- приведенная длина физического маятника, - ускорение свободного падения, - расстояние между точкой подвеса и центром масс маятника, 
- момент инерции маятника относительно оси, проходящей через точку подвеса.
Дифференциальное уравнение затухающих колебаний пружинного маятника:
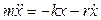или
,
где 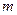- масса маятника, - коэффициент упругости пружины, 
- коэффициент сопротивления среды,
- коэффициент затухания, - циклическая частота свободных незатухающих колебаний.
Решение дифференциального уравнения затухающих колебаний: 
,
где 
- амплитуда затухающих колебаний, 
- амплитуда колебаний в момент времени = 0,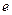 
- основание натурального логарифма, 
- коэффициент затухания,
- начальная фаза затухающих колебаний.
Циклическая частота затухающих колебаний: 
.
Логарифмический декремент затухания: 
,
где - период затухающих колебаний, 
- время релаксации, 
- число колебаний, совершаемых за время уменьшения амплитуды в 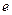раз.
ВОЛНОВЫЕ ПРОЦЕССЫ
Длина гармонической волны: 
,
где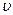 
- скорость распространения волны, - период колебаний физических величин в данной точке пространства.
Для всех типов волн скорость их распространения: 
,
где 
- линейная частота колебаний физических величин.
Уравнение плоской гармонической волны, распространяющейся вдоль положитель-ного направления оси O 
: 
,
где 
- колеблющаяся физическая величина, - амплитуда колеблющейся физической величины, 
- фаза волны, 
- циклическая частота,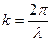 
- волновое число, - начальная фаза волны.
Уравнения плоской монохроматической электромагнитной волны, распространяющейся вдоль положительного направления оси O :
,
,
где 
- проекция вектора 
напряженности электрического поля на ось O 
, 
- проекция вектора 
напряженности магнитного поля на ось O 
, 
и 
- амплитуды, соответственно, электрического и магнитного полей.
Две волны называются когерентными, если разность их фаз остается постоянной во времени: 
.
Когерентные волны имеют одинаковые частоты: 
.
При наложении в пространстве двух когерентных волн происходит увеличение или уменьшение амплитуды результирующей волны в разных его точках. Это явление называется интерференцией волн.