Главная | Обратная связь

Функціональні ряди. Степеневі ряди

 

Нехай задана нескінченна послідовність функцій

що мають спільну область визначення .

Вираз вигляду

 

 

називається функціональним рядом.

Функції називаються членами ряду 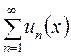, – загальним або м членом ряду.

Множина значень змінної , при яких відповідний числовий ряд збіжний, називається областю збіжності функціонального ряду.

Сумою функціонального ряду називається функція , якщо

 

, де .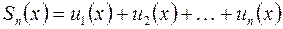

 

Степеневим рядом називається функціональний ряд виду

 

,

 

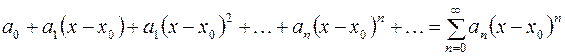де – дійсні числа, які називаються коефіцієнтами степеневого ряду.

 

Зокрема, при одержуємо ряд за степенями :

 

 

Т е о р е м а А б е л я.

Якщо степеневий ряд 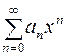збігається при деякому значенні , то він абсолютн6о збіжний для всіх значень , що задовольняють нерівність . Якщо ряд 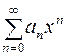розбіжний при деякому , то він розбіжний для всіх таких, що .

 

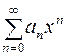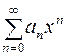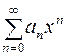Радіусом збіжності степеневого ряду називається таке число , що для всіх , які задовольняють умову , степеневий ряд збігається, а для всіх таких, що , ряд розбіжний.

Радіус збіжності знаходиться за формулами

(2)

або

(3)

Інтервал 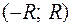, де – радіус збіжності степеневого ряду 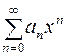, називається інтервалом збіжності цього ряду.

Питання про збіжність чи розбіжність степеневого ряду 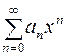на кінцях інтервалу збіжності (тобто при ) вирішується окремо шляхом дослідження на збіжність числових рядів та . Таким чином, область збіжності степеневого ряду 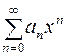може відрізнятися від інтервалу збіжності 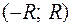не більше ніж двома точками .

У деяких степеневих рядів інтервал збіжності вироджується в точку , у інших охоплює всю числову вісь . Для таких рядів вважають відповідно, що і .

Радіус збіжності степеневого ряду знаходиться за формулами (2), (3), а інтервал збіжності такого ряду визначається з нерівності і має вигляд .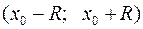

 

Приклад. Знайти радіус та область збіжності степеневого ряду

.

Розв’язання. Знайдемо радіус збіжності даного степеневого ряду, для чого скористаємося формулою

.

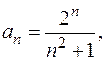тоді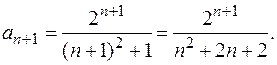

Отже, радіус збіжності ряду . Таким чином, інтервал збіжності степеневого ряду .

Дослідимо збіжність ряду на кінцях інтервалу.

При маємо знакозмінний числовий ряд . Дослідимо його за ознакою Лейбніца. Розглянемо абсолютні величини членів ряду

, тобто ,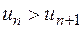

отже, члени ряду утворюють монотонно спадну послідовність.

Оскільки обидві умови ознаки Лейбніца виконуються, ряд збіжний.

При 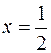отримаємо числовий ряд з додатними членами

.

Дослідимо його на збіжність з допомогою інтегральної ознаки Коші.

Загальний член ряду має вигляд . Розглянемо функцію , яка є неперервною і спадною на проміжку . Дослідимо на збіжність невласний інтеграл 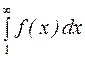. Маємо

Невласний інтеграл збіжний, тому і заданий ряд збіжний.

Таким чином, областю збіжності степеневого ряду є відрізок .