Главная | Обратная связь

Навигационные системы отсчета. Основные навигационные элементы полёта летательного аппарата. Способы решения навигационных задач.

2.1.Навигационные системы отсчёта.

Для определения и изучения характера движения ЛА необходимо проанализировать его положение и перемещение относительного другого тела или связанной с ним системы координат. В зависимости от масштабов перемещений ЛА системы отсчёта могут быть местными, глобальными и космическими.

Местные системы координат, начало которых связывается с Землей, используется в качестве систем отсчёта при сравнительно небольших перемещениях, когда поверхность Земли можно считать плоской.

В качестве примера приведём местную сферическую систему координат (рис.2).

В такой системе ось ОХ совмещают с северным направлением меридиана, проходящего через радионавигационную точку (РНТ), в которой установлена наземная радионавигационная аппаратура. Ось OY направляют по местной вертикали, а ось OZ проводят в горизонтальной плоскости. Место ЛА в системе координат определяется дальностью Д, азимутом и углом места .

В навигации ЛА используются следующие прямоугольные системы координат (рис.3):

нормальная земная система координат (НЗСК): O_g, X_g, Y_g, Z_g;

нормальная система координат (НСК): O, X_g, Y_g, Z_g;

связанная система координат (ССК): O, X, Y, Z.

 

Начало НЗСК фиксировано по отношению к Земле, ось O_gY_g проходит по местной вертикали, а оси O_gX_g, O_gZ_g направляются в горизонтальной плоскости в соответствии с решаемой задачей.

Начало НСК и ССК совмещается с центром масс ЛА.

Оси НСК (O, X_g, Y_g, Z_g) направляются параллельно осям НЗСК.

Оси ССК совмещаются со строительными осями самолёта. Оси OX и OY ССК, называемые соответственно продольной и нормальной осями, лежат в плоскости симметрии самолёта, а боковая ось OZ – перпендикулярна этой плоскости. Перемещение ЛА относительно своего центра масс характеризуется изменением положения осей ССК ЛА относительно НСК. Положение осей ССК определяется углами рыскания , тангажа и крена .

Угол рыскания ( ) – угол между осью OX_g и проекцией продольной оси ЛА на горизонтальную плоскость OX_gZ_g. Положительное направление отсчёта угла – влево от оси OX_g.

Угол тангажа ( ) – угол между продольной осью ЛА и горизонтальной плоскостью. Положительное направление отсчёта угла – вверх от горизонтальной плоскости.

Угол крена ( ) – угол между боковой осью ЛА и горизонтальной плоскостью. Положительное направление отсчёта угла – при правом крене.

Задание конечного положения ССК производится последовательным поворотом её вокруг осей OY, OZ и OX на углы , и соответственно.

Глобальные системы координат жёстко связаны с Землёй и применяются для воздушной навигации, охватывающей всю или значительную часть земной поверхности. Наиболее распространенными глобальными системами координат являются: географическая, геоцентрическая, а также левая и правая ортодромические системы координат.

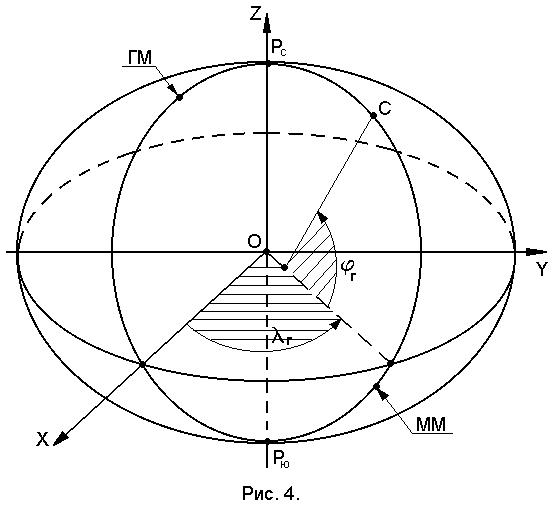
В географической системе координат за поверхность Земли принимают поверхность эллипсоида вращения (Крассовского). Положение точки на поверхности эллипсоида определяется геодезическими координатами – широтой и геодезической долготой 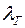(рис.4).

Геодезической широтой точки называется угол между нормалью к поверхности эллипсоида в этой точке и плоскостью экватора. Широта отсчитывается от плоскости экватора к северному Р_с и южному Р_ю полюсам от до .

Геодезической долготой 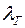называют двугранный угол, заключённый между плоскостями Гринвичского меридиана (ГМ-Гринвичский меридиан, нулевой меридиан, земной меридиан, проходящий через ось пассажного инструмента Гринвичской обсерватории. Город Гринвич — место расположения старой Гринвичской астрономической обсерватории в предместье города Лондон) и местного меридиана (ММ) точки С. Долгота измеряется либо центральным углом в плоскости экватора, либо дугой экватора в пределах от до 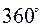. Долгота, отсчитываемая в восточном направлении, имеет знак плюс, а в западном – минус.

На топографические карты наносятся меридианы и параллели геодезической системы координат, поэтому положение точек на земной поверхности принято определять геодезическими координатами. Хотя поверхность земного эллипсоида имеет строгое математическое описание, но формулы, описывающие решение задач воздушной навигации, оказывается столь сложным, что практически могут быть реализованы лишь с помощью БЦВМ. Поэтому модель Земли упрощают, представляя её в виде шара радиусом 6 371 110 м.

Система координат, в которой Земля представляется в виде шара, называется геоцентрической. Отсчёт геоцентрической широты производится между плоскостью экватора и направлением радиуса – вектора. Способ отсчёта геоцентрической долготы совпадает со способом отсчёта географической долготы. Однако даже и в этом случае требуются сложные программы при решении навигационных задач, и реализации их в БЦВМ, так как в формулы входят тригонометрические функции координат и . При решении задач воздушной навигации вблизи экватора в полосе + 400-900 км при допустимых погрешностях 0,2-1 % можно записать: sin ≈0, . В этом случае навигационные формулы существенно упрощаются.

Для решения навигационных задач по упрощённым алгоритмам в районах, удалённых от экватора, используются произвольные сферические координаты, называемые ортодромическими. Подробнее ортодромическая система координат будет рассмотрена при изучении радиотехнической системы ближней навигации.

 

Рис. 4а Ортодромическая система координат.

Ортодромическая сферическая система координат (ОСК) с сеткой ортодромических параллелей и меридианов и «северным» полюсом ортодромическим Ро подобна географической, но повернута относительно нее, как это поясняется на рисунке 4 а. Ортодромический экватор (ОЭ) проходит обычно через две характерные точки маршрута 1 и 2, например соседние поворотные пункты маршрута (ППМ). Название системы связано с термином «ортодромия». Так называют дугу большого круга на сферической поверхности Земли, т. е. линию кратчайшего расстояния между двумя точками на земной сфере.

Координатами точки М местоположения в рассматриваемой системе служат ортодромические широта Ф и долгота . Широта отсчитывается от плоскости ортодромического экватора (ортодромии), а долгота — от точки А пересечения ортодромического и географического экваторов (ГЭ).

Ортодромическая система координат основная в самолетовождении и современных навигационных системах. Заданный маршрут обычно программируют из нескольких ортодромических этапов, называемых частными ортодромиями. При этом на каждом этапе используют свою ОСК, причем широта Ф характеризует боковое отклонение от заданной ортодромической траектории.

2.2. Основные навигационные элементы полёта ЛА

Навигационные элементы (параметры) характеризуют положение и перемещение ЛА.

2.2.1.Угловые навигационные элементы

В горизонтальной плоскости определяется весьма важный для навигации параметр – угол курса. Курсом ЛА называется угол в горизонтальной плоскости между северным направлением меридиана, походящего через центр масс ЛА и проекцией продольной оси ЛА (ОХ). Курс отсчитывается по часовой стрелке от северного направления в пределах от до 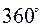. В зависимости от направления, выбранного для начала отсчёта, различают следующие разновидности определения курса (рис.5):

Истинный курс (ИК), отсчитывается от северного направления географического меридиана С_И, проходящего через центр масс ЛА;

Магнитный курс (МК), отсчитывается от северного направления магнитного меридиана С_М, проходящего через центр масс ЛА;

Компасный курс (КК), отсчитывается от северного направления С_К, указываемого самолётным магнитным компасом.

Разность между ИК и МК, вызванная несовпадением географического и магнитного полюсов Земли, называется магнитным склонением . Разность между магнитным и компасным курсом называется девиацией компаса и представляет собой инструментальную погрешность в показаниях магнитного компаса, вызываемую искажением магнитного поля Земли за счёт влияния ферромагнитных материалов.

В ряде случаев требуется определить угловое положение какой либо радионавигационной точки (РНТ) относительно продольной оси ЛА (рис.6).

Курсовым углом радиоориентира (КУР) называется угол между проекцией продольной оси ЛА на горизонтальную плоскость и направлением на РНТ.

Пеленгом радиоориентира относительно ЛА называют угол в горизонтальной плоскости между северным направлением меридиана, проходящего через центр масс ЛА и направлением на РНТ. Различают истинный пеленг радиостанции (ИПР) и магнитный пеленг радиостанции (МПР), которые связаны зависимостью:

(1).

В РНТ можно определить истинный пеленг ЛА. Истинный пеленг самолёта (ИПС) – угол в горизонтальной плоскости между северным направлением меридиана, проходящего через РНТ, и направлением на ЛА:

(2)

где: – соответствует расположению ЛА западнее РНТ;

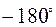– восточнее РНТ.

Значение поправки берётся из таблиц для заданной разности географических долгот места самолёта и радиостанции в зависимости от типа картографической проекции или непосредственно с карты.

2.2.2. Скорость и высота полёта ЛА

Различают воздушную, земную, путевую и вертикальную скорости ЛА.

Воздушной скоростью называется скорость полёта ЛА относительно воздушной среды.

Земная скорость называется скорость полёта ЛА относительно НЗСК. Она равна векторной сумме воздушной скорости ЛА и переносной скорости его движения вместе с воздушной средой (скорости ветра) относительно НЗСК, т.е. W_g = + (3)

В навигации под скоростью ветра понимают скорость горизонтального перемещения воздушных масс.

Путевая скорость ЛА называется составляющая вектора земной скорости в горизонтальной плоскости.

Вертикальная составляющая вектора W_Y – это скорость подъема или спуска ЛА.

Проекцию треугольника, составленного векторами скоростей W_g, , полёта ЛА, на горизонтальную плоскость называют навигационным треугольником скоростей (рис.7). Для простоты полёт ЛА считаем горизонтальным.

МПУ – магнитный путевой угол; ИПУ – истинный путевой угол;

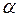– угол сноса ЛА.

Высотой полёта ЛА Н называется расстояние между центром масс ЛА и земной поверхностью, измеренное по вертикали.

Различают абсолютную, истинную, относительную и условную барометрическую высоты (рис.8).

Абсолютная высота полёта – это высота, отсчитываемая от среднего уровня Балтийского моря.

Истинная высота – это действительное расстояние от нижней точки ЛА до ближайшей точки на земной поверхности. Измеряется с помощью радиовысотомеров.

Относительная высота отсчитывается барометрическим высотомерами по отношению к уровню аэродромов взлёта или посадки. Информация об этой высоте устанавливается при взлёте либо заходе на посадку по барометрическому высотомеру.

Условная барометрическая высота – отсчитывается по показаниям барометрического высотомера от условного уровня, соответствующего давлению 760 мм рт. ст., на который устанавливается нуль шкалы высотомера. Эта высота принята основной для выдерживания экипажами заданных уровней полёта на маршруте, называемых эшелонами.

Кроме того, в воздушной навигации при выборе траектории полёта ЛА, расчёте и определении их текущих координат выполняют геометрические построения, основанные на использовании так называемых линий положения ЛА.

Линией положения называется ГМТ положения ЛА, определяемых постоянным значением одного из измеряемых навигационных параметров. 2.3 Способы решения навигационных задач

Способы решения навигационных задач подразделяются на способы определения МПЛА и способы полёта ЛА по заданной траектории.

Для определения МПЛА применяются различные способы, которые можно разделить на три группы:

обзорно-сравнительные способы (визуальная ориентировка: сравнение телевизионных, радиолокационных и других изображений местности с соответствующими картами);

способы линий положения с использованием радиотехнических систем;

способы счисления пути (доплеровское, воздушное, инерциальное и их комбинации).

Для обеспечения полёта ЛА по заданной траектории необходимо непрерывно или дискретно управлять его движением.

 

Способы вывода ЛА в заданную точку в зависимости от того, по какому параметру осуществляется управление полётом или в какой системе координат решаются основные задачи навигации, а также от дальности полёта ЛА и требуемой точности различают: маршрутный, путевой и курсовой.

В маршрутном способе задача навигации решается с использованием ортодромической системы координат, одной из осей которой служит линия заданного пути. Для управления полётом в этом случае непрерывно измеряются боковое уклонение Z от линии заданного пути (ЛЗП) и оставшееся расстояние S до заданной точки (ЗТ). Также необходимо знать время выхода ЛА в ЗТ (рис.9).

При путевом способе (рис.10) необходимо измерять курс ЛА ( ), заданный путевой угол ( ), угол сноса ( ).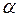

Параметр рассогласования определяется как:

(4)

При курсовом способе (рис.11) необходимо непрерывно измерять параметр ( ).

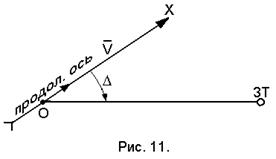В этом случае координаты ЛА, угол сноса, путевая скорость могут быть неизвестны. Такой способ может быть реализован с помощью автоматического радиокомпаса.

Способы определения МПЛА подробнее будут рассмотрены при изучении конкретного оборудования.