Главная | Обратная связь

Разложение функции в ряд Тейлора

 

Разложение математических функций в ряд Тейлора позволяет определить функция taylor, например:

 

>> syms x

>> taylor(sin(x))

ans =

x^5/120 - x^3/6 + x

 

По умолчанию выводятся шесть членов ряда разложения в окрестностях точки ноль. Число членов разложения можно задать во втором дополнительном параметре. Точка, в окрестности которой проводится разложение, указывается в третьем входном аргументе.

Например, получим 8 членов разложения функции в окрестности точки .

>> g=taylor(sin(x),8,1)

ans =

sin(1) - (sin(1)*(x - 1)^2)/2 + (sin(1)*(x - 1)^4)/24 - (sin(1)*(x - 1)^6)/720 + cos(1)*(x - 1) - (cos(1)*(x - 1)^3)/6 + (cos(1)*(x - 1)^5)/120 - (cos(1)*(x - 1)^7)/5040

 

Это соответствует выражению

Убедимся в то, что в точке значения функции и ряда Тейлора совпадают:

 

>> subs(g,x,1)

ans =

0.8415

 

>> sin(1)

ans =

0.8415

 

Для более наглядного представления функции можно использовать функцию pretty:

 

>> pretty(g)

 

Так как ряд Тейлора представляет собой полином, то всегда можно перейти от символьного представления к векторному

 

>> v=sym2poly(g)

ans =

-0.0001 -0.0004 0.0093 -0.0012 -0.1656 -0.0005 1.0002 -0.0000

 

и построить график функции на заданном отрезке

 

>> x=0:0.001:2;

>> f=polyval(v,x);

>> plot(x,f)

 

С увеличением числа членов ряда растет точность приближения исходной функции в окрестности точки, относительно которой проводится разложение. На рис. 1-2 представлены графики функции и рядов Тейлора для данной функции с заданным числом членов разложения.

Рис. 1. Графики функции и ее аппроксимации

Рис. 2. Графики функции и ее аппроксимации вблизи точки, относительно которой происходит разложение в ряд Тейлора

 

Для оценки точности аппроксимации функции рядом Тейлора на заданном отрезке может служить следующий подход.

Задаем число членов ряда n.

1. Разбиваем отрезок на узлов . i=1..N, число узлов выбирается достаточно большим.

2. Для каждого узла i=1:N находим значения исходной функции и ряда Тейлора степени n и находим ошибку аппроксимации для данной точки

.

3. Критериями точности аппроксимации могут быть следующие целевые функции: средний модуль ошибки

,

или средний квадрат ошибки

.

И в том, и в другом случае, чем ближе значение критерия к нулю, тем точнее аппроксимация.

 

В состав Symbolic Math Toolbox входит приложение taylortool с графическим интерфейсом, предназначенное для наглядной демонстрации разложения в ряд различных функций, в том числе и определенных пользователем. Команда taylortool приводит к появлению окна приложения, изображенного на рис. 3.

 

Рис. 3. Пример работы приложения taylortool. Синим показана исходная функция, а красным – частичная сумма ряда Тейлора

 

Пользователь может вводить формулы различных функций в строке f(x)= в соответствии с правилами MATLAB и исследовать приближение функции на произвольном интервале отрезком ряда Тейлора, содержащим различное число членов разложения. Интерфейс приложения taylortool достаточно простой и не требует дополнительных пояснений.

 

Пример 2. Построим график ошибки и модуля ошибки для функции f=sin(x) при использовании аппроксимации полиномом третьей степени на отрезке [-2; 2].

 

% интервал разбиения с небольшим шагом

t=-2:0.01:2;

N=numel(t); % число узлов разбиения

% исходная функция

f=sin(t);

 

syms x

% частичная сумма ряда Тейлора при n=3 g(x,3)

g3=taylor(sin(x),3,0);

g=subs(g3,x,t);

% график функции и ее разложения в ряд Тейлора

% figure

% plot(t,f,t,g)

% grid on

% ошибка аппроксимации

e=f-g;

% абсолютное значение ошибки аппроксимации

e1=abs(e);

% графики ошибки и модуля ошибки

figure

plot(t,e,t,e1)

grid on

legend('e','e_1')

 

% целевая функция

eps1(i)=sum(e1)/N;

 

Задание 1.

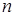Найти разложения Тейлора заданной функции (табл. 1) в точке при числе слагаемых от 1 до 4 с помощью приложения taylortool и функции taylor.

 

Табл. 1. К заданию 3.

№
		sinh(x)		[-1; 3]
		cosh(x)		[0; 4]
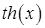
		tahg(x)	-0.5	[-1; 1]
		sqrt(1+x)	0.5	[-0.5; 1]
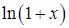
		log(1+x)	0.2	[-0.5; 1]
		exp(x)		[-1; 3]
		cos(x)		[0; 4]
		sin(x)	1.5	[-1; 4]
		sec(x)	0.2	[-1;1]
		asin(x)	-0.2	[-1;1]

 

Построить графики исходной функции, рядов Тейлора (на одних осях, как на рис. 1) и ошибки аппроксимации при n=1..4 на интервале . При этом все графики должны иметь разный стиль оформления (цвет и тип линий, тип маркера и т.д.).

Найти значения целевых функций , на заданном интервале для n=1..8. Полученные результаты занести в табл. 2.

Постройте графики целевых функций в логарифмическом масштабе. Для этого вместо функции plot используйте функцию semilogy.

Сделайте вывод о влиянии числа членов разложения на точность аппроксимации.

 

Табл. 2. Зависимость ошибки аппроксимации от числа членов разложения в ряд Тейлора.

…