 |
|
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ (МОМЕНТЫ) СЛУЧАЙНЫХ ПРОЦЕССОВ
Одномерная плотность вероятности
= 
.
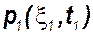статистически полностью характеризует случайный процесс x(t) в любом конкретном сечении, например, t1. Аналогично находятся одномерные плотности вероятностей и для других сечений - p1(x2,t2). . . p1(xn,tn).
Более полную характеристику случайного процесса даёт двумерная плотность вероятности, рассматривающая значения реализаций в сечениях t1..и t2 взаимосвязано:
где py(x2,t2½x1,t1) - условная плотность вероятности в сечении t2 относительно сечения t1.
Рассматривая совместно n сечений случайного процесса, можно найти n-мерную или многомерную плотность вероятности 
.
Многомерная плотность вероятности является наиболее полной характеристикой случайного процесса, причем тем более точной, чем больше число сечений n.
У простейшей разновидности случайных процессов – абсолютно случайного процесса – значенияxв разных сечениях считаются невзаимозависимыми (некоррелированными). Для него n-мерная плотность вероятности полностью определяется безусловными одномерными плотностями вероятностей всех сечений:
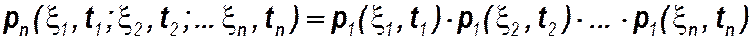
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ (МОМЕНТЫ) СЛУЧАЙНЫХ ПРОЦЕССОВ
В основе определения числовых характеристик – моментов случайных величин – также лежит понятие среднего арифметического, причём усреднение проводят по множеству реализаций (по ансамблю).
Если случайная величина xi принимает m1 раз значение x1(1), m2 раз – значение x1(2), . . . mn раз – значение x1(n), то среднее арифметическое при m2 + m2 + …+ mn =M будет
x i ср.ар.= 
= 
.
При достаточно большом М можно принять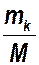 
= pk . Тогда
xi ср.ар = 
.
При непрерывном распределении значений случайной величины переходят от суммы к интегралу:
· Для случайного процесса среднее по множеству значение, называемое математическим ожиданием случайной величины x, определяется как начальный момент первого порядка:
.
Характеризует среднее значение соответствующих сечений процесса и меняется для различных сечений, но уже не является случайной величиной.
· Начальный момент второго порядка (или математическое ожидание квадрата случайной величины) 
.
Называется средним ква-драта и определяет в широком смысле среднюю мощность случайной величины, а
представляет собой среднеквадратичное значение x(t).
· Если рассматривать отклонение случайного процесса от математического ожидания-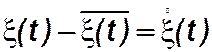 
, то получим центрированный процесс, характеризующийся центральнымимоментами. При этом центральный момент первого порядка равен нулю (среднее значение отклонения математического ожидания от него самого)
· Центральный момент второго порядка
[М( 
)]=M{[ 
]2} 
называется дисперсией и определяет среднее квадрата или мощность отклонений x(t) от математического ожидания. А среднее квадратическое отклонение 
характеризует разброс случайного процесса x(t) вокруг его математического ожидания.
Аналогично находятся моменты более высоких порядков, которые, как и математическое ожидание mx,и дисперсия Dx = sx 2, также являются неслучайными величинами и характеризуют поведение случайного процесса в отдельных сечениях.
· Количественно связь между сечениями t1 и t2 устанавливается смешанным центральным моментом второго порядка (математическим ожиданием произведения центрированных величин):
.
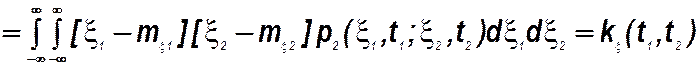Эта характеристика называется корреляционной функцией и зависит от двух переменных t1 и t2. Если kx(t1,t2) характеризует один и тот же случайный процесс, ее называют функцией автокорреляции. При kx(t1,t2)>0 значения x(t1) и x(t2) коррелированы (взаимосвязаны)
· Функция взаимной корреляции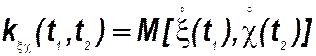 
устанавливает связь между сечениями двух случайных процессов x(t) и 
(t). При равенстве её нулю для любых значений аргументов случайные процессы некоррелированы.