 |
|
Функциональные последовательности и ряды
Числовые ряды.
 1º. Основные понятия.
1º. Основные понятия.
Пусть {z k} - некоторая последовательность чисел, вообще говоря, комп- лексных . Рассмотрим последовательность {S n}, где S 1 = z 1 , а при любом натуральном n > 1 S n = z 1 + z 2 + … + z n . Последовательность {S n} мо -жет оказаться либо сходящейся, либо расходящейся.
Пусть последовательность {S n} сходится, а S есть ее предел: lim S n = S . Будем говорить в этом случае, что числовой ряд
z 1 + z 2 + … + z k + … ( 1 )
сходится, а число S назовем суммой этого ряда. Члены последовательности {z k} назовем членами ряда (1) ; S n назовем его n – ой частичной суммой .
Замечание. Хотя число S и называют суммой, на самом деле оно не явля- ется суммой в привычном понимании этого термина, согласно которому сумма - это результат сложения некоторого конечного количества слагаемых. Суммой является. например, всякий член последовательности {S n}, начиная с S 2 . Но сложить бесконечное множество членов ряда невозможно, и число S представляет собой результат другого математического действия – преде- льного перехода, примененного к последовательности сумм {S n}.
Для обозначения ряда (1) мы обычно будем пользоваться символом  , а также упрощенным символом
, а также упрощенным символом  . В этих символах z k называют общим членом ряда. Если ряд сходится, а S является его суммой, т.е. если lim Sn = S, будем записывать:
. В этих символах z k называют общим членом ряда. Если ряд сходится, а S является его суммой, т.е. если lim Sn = S, будем записывать:  = S.
= S.
В случае, когда последовательность {S n} расходится, будем говорить, что ряд (1) расходится; суммы такой ряд не имеет. Однако, если S n → + ∞ или S n → - ∞ , принято говорить. что сумма расходящегося ряда (1) равна + ∞ или - ∞ соответственно.
Пример 1. Пусть q – некоторое комплексное число; положим при вском натуральном k z k = q  и рассмотрим ряд
и рассмотрим ряд  = 1 + q + q
= 1 + q + q  +…+ q
+…+ q  + ... ( его члены образуют геометрическую прогрессию). Имеем: S n = 1 + q + q
+ ... ( его члены образуют геометрическую прогрессию). Имеем: S n = 1 + q + q  + … + q
+ … + q  =
=  . Если |q| < 1, то
. Если |q| < 1, то  → 0 и, значит, S n
→ 0 и, значит, S n  ; если же |q | > 1, то q
; если же |q | > 1, то q 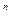 → ∞ и , следовательно, S n
→ ∞ и , следовательно, S n  . Итак, при |q| < 1 рассматриваемый
. Итак, при |q| < 1 рассматриваемый
ряд сходится, его сумма равна 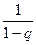 ; при |q | > 1 ряд расходится.
; при |q | > 1 ряд расходится.
Пример 2. Рассмотрим ряд  . Здесь z k =
. Здесь z k =  , Sn = =
, Sn = =  =
=  ln2 + ( ln3 – ln2) + (ln4 – ln3) + … + ( ln n – ln(n-1)) + + ( ln(n+1) – ln n ) = ln (n+1). Очевидно, S n→ +∞ . Значит, ряд расходится, его сумма равна + ∞.
ln2 + ( ln3 – ln2) + (ln4 – ln3) + … + ( ln n – ln(n-1)) + + ( ln(n+1) – ln n ) = ln (n+1). Очевидно, S n→ +∞ . Значит, ряд расходится, его сумма равна + ∞.
Пример 3. Пусть z k =(-1)  , S n =
, S n =  1 – 1 + … …+ (-1)
1 – 1 + … …+ (-1)  . При четных n эта сумма равна нулю, а при нечетных – единице ; значит, последовательность {S n} частичных сумм ряда
. При четных n эта сумма равна нулю, а при нечетных – единице ; значит, последовательность {S n} частичных сумм ряда  не имеет предела, ни конечного, ни бесконечного. Ряд расходится.
не имеет предела, ни конечного, ни бесконечного. Ряд расходится.
2˚. Общие свойства числовых рядов
1. ( Критерий сходимости Коши) Для того, чтобы числовой ряд  сходился, необходимо и достаточно, чтобы для всякого положительного ε можно было указать натуральное n ε такое,что при всех натуральных n > n ε и любых натуральных р справедливо неравенство
сходился, необходимо и достаточно, чтобы для всякого положительного ε можно было указать натуральное n ε такое,что при всех натуральных n > n ε и любых натуральных р справедливо неравенство  .
.
► Сходимость числового ряда означает сходимость последовательности {S n} его частичных сумм. Напомним формулировку критерия Коши сходимости последовательности : для того, чтобы последовательность {S n} сходилась, необходимо и достаточно, чтобы
 .
.
Не ограничивая общности можно считать, что m > n , т.е. что m = n + p , где р - некоторое натуральное число. Если n > n ε, то подавно n + p > n ε , поэтому написанную выше строчку можно заменить следующей, ей равно- сильной :
 .
.
Заметим :  ; Таким образом, из критерия Коши для последовательности {S n} вытекает: ряд
; Таким образом, из критерия Коши для последовательности {S n} вытекает: ряд  сходится тогда и только тогда, когда
сходится тогда и только тогда, когда

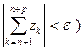 ,
,
что и требовалось доказать. ◄
Приведем пример применения критерия Коши.
Пример 4, Ряд  называют гармоническим рядом. Покажем, что это расходящийся ряд. Пусть n - некоторое натуральное число; а p = n +2 . Рассмотрим
называют гармоническим рядом. Покажем, что это расходящийся ряд. Пусть n - некоторое натуральное число; а p = n +2 . Рассмотрим  В этой сумме n +2 слагаемых, причем
В этой сумме n +2 слагаемых, причем  - наименьшее из них ; поэтому
- наименьшее из них ; поэтому 
 Здесь n - любое натуральное число. Зададим ε, удовлетворяющее неравенствам 0 < ε < ½ . Тогда при всяком натуральном n и p = n +2 будет выполнено
Здесь n - любое натуральное число. Зададим ε, удовлетворяющее неравенствам 0 < ε < ½ . Тогда при всяком натуральном n и p = n +2 будет выполнено  , а это означает, что для такого ε нельзя указать n ε , которое удовлетвори- ло бы требованию критерия сходимости Коши . Значит, ряд расходится. ◄
, а это означает, что для такого ε нельзя указать n ε , которое удовлетвори- ло бы требованию критерия сходимости Коши . Значит, ряд расходится. ◄
2. ( Необходимое условие сходимости ) Если ряд  .сходится, то его общий член стремится к нулю : z k → 0 .
.сходится, то его общий член стремится к нулю : z k → 0 .
► Пусть S n =  . Обозначим сумму ряда через S : S n → S. При всяком n ≥2 , очевидно, z n = S n - S n -1 . Перейдем в этом равенстве к пределу ; так как последовательности
. Обозначим сумму ряда через S : S n → S. При всяком n ≥2 , очевидно, z n = S n - S n -1 . Перейдем в этом равенстве к пределу ; так как последовательности  имеют один и тот же предел S , получим : z n → 0. ◄
имеют один и тот же предел S , получим : z n → 0. ◄
Замечание. Обратное утверждение (если z k → 0 , то  сходится ) неверно. Действительно, для гармонического ряда имеем z k → 0 , однако ряд расходится. Можно указать еще и на ряд
сходится ) неверно. Действительно, для гармонического ряда имеем z k → 0 , однако ряд расходится. Можно указать еще и на ряд  , рассмотренный выше (см. пример 2 ): его общий член,очевидно, стремится к нулю, но ряд расходится.
, рассмотренный выше (см. пример 2 ): его общий член,очевидно, стремится к нулю, но ряд расходится.
3. ( Достаточное условие расходимости ) Если общий член ряда не стремится к нулю, то ряд расходится.
► Действительно, если общий член ряда не стремится к нулю, ряд не может оказаться сходящимся, так как общий член сходящегося ряда обязательно стремится к нулю. ◄
Пример 5. Выше ( см. пример 1) мы показали, что ряд  сходится, если |q| < 1 и расходится, если |q| > 1. Рассмотрим случай |q| = 1. Имеем :
сходится, если |q| < 1 и расходится, если |q| > 1. Рассмотрим случай |q| = 1. Имеем :  при всяком натуральном k, поэтому последовательность
при всяком натуральном k, поэтому последовательность 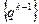 заведомо не стремится к нулю; значит. при любом комплексном q, |q| = 1, рассматриваемый ряд расходится.
заведомо не стремится к нулю; значит. при любом комплексном q, |q| = 1, рассматриваемый ряд расходится.
4. ( Умножение числа на ряд) Пусть заданы ряд  и некоторое отличное от нуля число λ , вообще говоря , комплексное. Произведением числа λ на ряд
и некоторое отличное от нуля число λ , вообще говоря , комплексное. Произведением числа λ на ряд  называют ряд
называют ряд  , где wk = λzk . Справаедливы утверждения: 1) ряды
, где wk = λzk . Справаедливы утверждения: 1) ряды  и
и 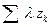 либо оба сходятся, либо оба расходятся ; 2) если
либо оба сходятся, либо оба расходятся ; 2) если  = S, то
= S, то 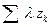 = λ S.
= λ S.
► Пусть n - некоторое натуральное число. Обозначим : 
 . Очевидно,
. Очевидно,  .Отсюда и из теоремы об арифметических действиях со сходящимися последовательностями ( [3], п. 3.5) вытекает : 1) последовательности частичных сумм
.Отсюда и из теоремы об арифметических действиях со сходящимися последовательностями ( [3], п. 3.5) вытекает : 1) последовательности частичных сумм  либо обе сходятся, либо обе расходятся ; 2 ) если
либо обе сходятся, либо обе расходятся ; 2 ) если  ◄
◄
5. ( Сложение рядав ) Ряд  называют суммой рядов
называют суммой рядов 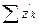 и
и  . Справедливы утверждения: 1) пусть ряды
. Справедливы утверждения: 1) пусть ряды  сходятся, причем
сходятся, причем  ; тогда сходится и
; тогда сходится и  , причем
, причем  =
=  ; 2) если один из рядов
; 2) если один из рядов  сходится, а другой расходится, то ряд
сходится, а другой расходится, то ряд  расходится.
расходится.
► Обозначим :  Очевидно,
Очевидно, 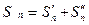 . Из теоремы об арифметических действиях со сходящимися последовательностями следует : 1) если последовательности частичных сумм
. Из теоремы об арифметических действиях со сходящимися последовательностями следует : 1) если последовательности частичных сумм  сходятся,
сходятся,  то сходится и их сумма - последовательность
то сходится и их сумма - последовательность  , причем Sn → →S’+S”; 2) если одна из последовательностей
, причем Sn → →S’+S”; 2) если одна из последовательностей  сходится , а другая расходится, то
сходится , а другая расходится, то  не может быть сходящейся последовательностью, значит, ряд расходится. ◄
не может быть сходящейся последовательностью, значит, ряд расходится. ◄
Замечание. Если оба ряда  расходятся, то их сумма, т.е. ряд
расходятся, то их сумма, т.е. ряд  может оказаться как сходящимся, так и расходящимся рядом. На- пример, положим
может оказаться как сходящимся, так и расходящимся рядом. На- пример, положим 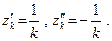 Тогда ряды
Тогда ряды  расходятся ( см. пример 4) , а ряд
расходятся ( см. пример 4) , а ряд  сходится, так как каждый его член равен нулю.
сходится, так как каждый его член равен нулю.
6. Пусть задан ряд  , а m - некоторое натуральное число . Ряд
, а m - некоторое натуральное число . Ряд  , где wl = = zm+l , т.е. ряд zm+1+zm+2+ …+ zm+l + … =
, где wl = = zm+l , т.е. ряд zm+1+zm+2+ …+ zm+l + … =  , называют остатком ряда
, называют остатком ряда  . Справедливо утверждение: ряд
. Справедливо утверждение: ряд  и его остаток
и его остаток  либо оба сходятся, либо оба расходятся.
либо оба сходятся, либо оба расходятся.
► Очевидно, при любом натуральном p  т.е.
т.е.  где А = =
где А = =  . Ввиду такой связи между последовательностями частичных сумм
. Ввиду такой связи между последовательностями частичных сумм 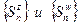 очевидно, что если сходится одна из них, то сходится и другая; если одна из них расходится, то другая не может быть сходящейся. ◄
очевидно, что если сходится одна из них, то сходится и другая; если одна из них расходится, то другая не может быть сходящейся. ◄
7. Пусть  и
и 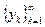 - последовательности вещественных чисел . Обозначим : zk = xk + i yk , Sn=
- последовательности вещественных чисел . Обозначим : zk = xk + i yk , Sn= 
 . Если ряды
. Если ряды  ,
,  сходятся, то их суммы обозначаем через S ,
сходятся, то их суммы обозначаем через S ,  и
и  соответственно. Справедливы утверждения: 1) ряд
соответственно. Справедливы утверждения: 1) ряд  сходится тогда и только тогда, когда сходятся оба ряда
сходится тогда и только тогда, когда сходятся оба ряда  ; 2) если
; 2) если  сходится, то S =
сходится, то S =  + i
+ i  .
.
► Заметим : Sn = S  + i S
+ i S  . Утверждения 1) и 2) вытекают непосредственно из свойств последовательностей комплексных чисел. ◄
. Утверждения 1) и 2) вытекают непосредственно из свойств последовательностей комплексных чисел. ◄
3º. Признаки сходимости рядов с неотрицательными членами.
Ряды находят разнообразные применения в прикладной математике. Имея дело с числовым рядом,прежде всего следует выяснить, сходится ли этот ряд. Выяснить это часто удается с помощью свойств, описанных в предыдущем пункте ( например, если общий член не стремится к нулю, то ряд расходится). Если указанных средств оказалось недостаточно, обращаются к признакам сходимости и расходимости рядов, наиболее употребительные из которых составляют содержание этого и следующего пунктов.
В этом пункте мы рассматриваем числовые ряды  члены которых неотрицательны. Обозначим через Sn частичную сумму такого ряда.: S n = =
члены которых неотрицательны. Обозначим через Sn частичную сумму такого ряда.: S n = =  .Так как a k ≥ 0, то S n ≤ S n +1, т.е. {S n } - монотонная неубывающая последовательность. Если эта последовательность ограничена сверху, она сходится, в противном случае она стремится к + ∞ ([3], п.3.6 ). Таким образом, справедлива следующая теорема.
.Так как a k ≥ 0, то S n ≤ S n +1, т.е. {S n } - монотонная неубывающая последовательность. Если эта последовательность ограничена сверху, она сходится, в противном случае она стремится к + ∞ ([3], п.3.6 ). Таким образом, справедлива следующая теорема.
Теорема 1.( Критерий сходимости ряда с неотрицательными членами) Для того, чтобы ряд  a k ≥ 0, сходился, необходимо и достаточно, что- бы последовательность его частичных сумм {S n } была ограничена сверху .
a k ≥ 0, сходился, необходимо и достаточно, что- бы последовательность его частичных сумм {S n } была ограничена сверху .
Пусть f - некоторая функция, определенная на промежутке [ 1, +∞). Обозначим : a k= f(k) , где k  , и рассмотрим числовой ряд
, и рассмотрим числовой ряд  . Будем называть f производящей функцией для числового ряда
. Будем называть f производящей функцией для числового ряда  . Например, f (x) =
. Например, f (x) = 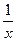 является производящей функцией для гармонического ряда
является производящей функцией для гармонического ряда  , так как при всех натуральных k f (k) =
, так как при всех натуральных k f (k) =  . Если производящая функция неотрицательна на [1, +∞), то
. Если производящая функция неотрицательна на [1, +∞), то  - ряд с неотрицатеьными членами.
- ряд с неотрицатеьными членами.
Теорема 2.(Интегральный признак Коши) Пусть производящая функция f числового ряда  непрерывна, неотрицательна и монотонно не возрастает на промежутке [1;+∞). Для того, чтобы ряд
непрерывна, неотрицательна и монотонно не возрастает на промежутке [1;+∞). Для того, чтобы ряд  был сходящимся, необходимо и достаточно, чтобы сходился несобственный интеграл
был сходящимся, необходимо и достаточно, чтобы сходился несобственный интеграл  .
.
► Напомним: по определению  =
= 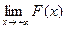 , где F(x) =
, где F(x) =  ; интеграл
; интеграл  сходится, если предел
сходится, если предел 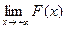 конечен, и расходится в противном случае, т.е. если этот предел равен ∞ или не существует ( [4], п. 2.1). По условию теоремы f (x) неотрицательна на [1, +∞) , поэтому F(x) моно -тонно не убывает [ 1,∞) ; следовательно,
конечен, и расходится в противном случае, т.е. если этот предел равен ∞ или не существует ( [4], п. 2.1). По условию теоремы f (x) неотрицательна на [1, +∞) , поэтому F(x) моно -тонно не убывает [ 1,∞) ; следовательно, 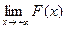 конечен тогда и только тог- да, когда F(x) ограничена на [ 1, +∞) сверху. Отметим еще, что если интег- рал
конечен тогда и только тог- да, когда F(x) ограничена на [ 1, +∞) сверху. Отметим еще, что если интег- рал  сходится, то F(x) ≤
сходится, то F(x) ≤  при всех х
при всех х  1.
1.
Пусть k – натуральное число. Так как f (x) - монотонная невозрастающая функция, то  т.е.
т.е.  при
при  Интегрируя последние неравенства, получим:
Интегрируя последние неравенства, получим:  , т.е.
, т.е. 
 . Отсюда:
. Отсюда:  , т.е.
, т.е.
 N Sn –an ≥
N Sn –an ≥  ≥ Sn –a1 (2)
≥ Sn –a1 (2)
Необходимость. Пусть  сходится, а S – его сумма : lim Sn = S, где
сходится, а S – его сумма : lim Sn = S, где  . Так как
. Так как  , то {Sn} – неубывающая последовательность, и при всяком натуральном n Sn ≤ Sn+1 ≤ S. Из (2) имеем:
, то {Sn} – неубывающая последовательность, и при всяком натуральном n Sn ≤ Sn+1 ≤ S. Из (2) имеем:  N
N  ≤ Sn –- an , и так как Sn ≤ S , то при всех натуральных n справедливо F(n) ≤ S. Отсюда вытекает: функция F ограничена на [1;+∞) cверху числом S; следователь- но (см. выше), интеграл
≤ Sn –- an , и так как Sn ≤ S , то при всех натуральных n справедливо F(n) ≤ S. Отсюда вытекает: функция F ограничена на [1;+∞) cверху числом S; следователь- но (см. выше), интеграл  сходится.
сходится.
Достаточность. Пусть интеграл  сходится. Так как F(x) ≤
сходится. Так как F(x) ≤  , то из (2) имеем: при всех натуральных n :
, то из (2) имеем: при всех натуральных n :  ≥ F(n) =
≥ F(n) =  ≥ Sn –a1 . Отсюда :
≥ Sn –a1 . Отсюда :  NSn ≤
NSn ≤  + а1 , т.е. последовательность {S n } ограниче- на сверху; значит ( см. теорему 1) , ряд
+ а1 , т.е. последовательность {S n } ограниче- на сверху; значит ( см. теорему 1) , ряд  сходится. ◄
сходится. ◄
Пример 6. Пусть λ – некоторое вещественное число.Рассмотрим ряд  . Этот ряд называют обобщенным гармоническим рядом ( в частном случае λ =1 получим гармонический ряд, см. пример 4). Если λ ≤ 0 , то
. Этот ряд называют обобщенным гармоническим рядом ( в частном случае λ =1 получим гармонический ряд, см. пример 4). Если λ ≤ 0 , то 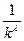 не стремится к нулю; значит (см. достаточное условие расходимости, 2˚), при λ≤0 обобщенный гармонический ряд расходится. Пусть λ>0. Функция f (x) = =
не стремится к нулю; значит (см. достаточное условие расходимости, 2˚), при λ≤0 обобщенный гармонический ряд расходится. Пусть λ>0. Функция f (x) = =  , очевидно, является производящей функцией для ряда
, очевидно, является производящей функцией для ряда  ; она положительна и убывает на [1;+∞) . Таким образом, f (x) удовлетворяет тре- бованиям интегрального признака Коши.
; она положительна и убывает на [1;+∞) . Таким образом, f (x) удовлетворяет тре- бованиям интегрального признака Коши.
Имеем: при λ≠ 1  , при λ = 1
, при λ = 1  . Из этих равенств нетрудно вывести, что
. Из этих равенств нетрудно вывести, что  расходится при 0 < λ ≤ 1 и сходится при λ > 1. По интегральному признаку Коши обобщенный гармонический ряд ведет себя так же.
расходится при 0 < λ ≤ 1 и сходится при λ > 1. По интегральному признаку Коши обобщенный гармонический ряд ведет себя так же.
Итак, ряд  расходится при λ ≤ 1 и сходится при λ > 1.
расходится при λ ≤ 1 и сходится при λ > 1.
Следующие теоремы дают достаточные условия сходимости или расходимости ряда с неотрицательными членами.
Теорема 3.( Первый признак сравнения ) Пусть {ak} и{bk} - две последовательности неотрицательных чисел, причем  . Тогда :
. Тогда :
1) если  сходится, то сходится и ряд
сходится, то сходится и ряд  ;
;
2) если ряд  расходится, то расходится и ряд
расходится, то расходится и ряд  .
.
► Обозначим :  1) Очевидно,
1) Очевидно,  Пусть
Пусть  сходится, а
сходится, а  - его сумма :
- его сумма : 
 . Так как последовательность частичных сумм монотонно не убывает, то
. Так как последовательность частичных сумм монотонно не убывает, то  ≤
≤  . Значит, при всех натуральных n
. Значит, при всех натуральных n  ≤
≤  , т.е. последовательность {
, т.е. последовательность {  } ограничена свер- ху числом
} ограничена свер- ху числом  , и поэтому она сходится. 2) Пусть
, и поэтому она сходится. 2) Пусть  расходится; тогда
расходится; тогда  Так как
Так как  , то и
, то и  → +∞, т.е. ряд
→ +∞, т.е. ряд  расходится.◄
расходится.◄
Пример 7. Рассмотрим ряд  . При всяком натуральном k k! ≥
. При всяком натуральном k k! ≥  Следовательно, при всех натуральных k
Следовательно, при всех натуральных k 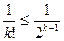 Ряд
Ряд  сходится (пример 1, q = = ½), значит,сходится и рассматриваемый ряд.
сходится (пример 1, q = = ½), значит,сходится и рассматриваемый ряд.
Теорема 3.( Второй признак сравнения ) Пусть {ak} – последовательность неотрицательных чисел, а {bk} – последовательность положительных чисел. Пусть, далее, 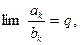 где q - либо неотрицательное число, либо символ +∞. Тогда :
где q - либо неотрицательное число, либо символ +∞. Тогда :
1) если 0 < q < + ∞, то ряды  и
и  ведут себя одинаково – либо
ведут себя одинаково – либо
оба сходятся, либо оба расходятся ;
2) если q = 0, а ряд  сходится, то сходится и ряд
сходится, то сходится и ряд  ;
;
3) если q = + ∞, а ряд  расходится, то расходится и ряд
расходится, то расходится и ряд  .
.
► 1) Достаточно показать, что из сходимости  вытекает сходи –
вытекает сходи –
мость  , а из расходимости
, а из расходимости  следует расходимость
следует расходимость  . Зададим
. Зададим
ε, 0 < ε < q . Найдется натуральное kε , такое, что при всех k > kε справедливо неравенство  , т.е.
, т.е.
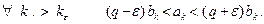 (3)
(3)
Пусть  сходится . Тогда сходится и его остаток
сходится . Тогда сходится и его остаток  . Из неравенств
. Из неравенств
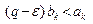 ( см.(3) ) и первого признака сравнения вытекает сходимость ряда
( см.(3) ) и первого признака сравнения вытекает сходимость ряда  ( заметим, что q – ε > 0 ). Этот ряд представляет собой остаток ряда
( заметим, что q – ε > 0 ). Этот ряд представляет собой остаток ряда  , который, следовательно, является сходящимся. Значит (см. свойство 4, п. 2º ),
, который, следовательно, является сходящимся. Значит (см. свойство 4, п. 2º ),  сходится.
сходится.
Пусть  расходится. Чтобы вывести отсюда расходимость ряда
расходится. Чтобы вывести отсюда расходимость ряда  ,
,
следует воспользоваться неравенствами 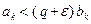 , справедливыми при k > > kε ( см. (3) ). Рассуждения аналогичны изложенным выше.
, справедливыми при k > > kε ( см. (3) ). Рассуждения аналогичны изложенным выше.
2) Пусть  сходится. Зададим некоторое ε > 0. Так как
сходится. Зададим некоторое ε > 0. Так как  най- дется kε , такое, что при всех k > kε справедливо неравенство
най- дется kε , такое, что при всех k > kε справедливо неравенство  , т.е.
, т.е.  Так как
Так как  сходится, то сходится и его остаток
сходится, то сходится и его остаток  . По свойству 4, п. 2º, сходится ряд
. По свойству 4, п. 2º, сходится ряд  . Отсюда и из первого признака сравнения вытекает сходимость ряда
. Отсюда и из первого признака сравнения вытекает сходимость ряда 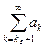 , который представляет собой остаток ряда
, который представляет собой остаток ряда  . Значит,
. Значит,  сходится.
сходится.
3) Пусть  расходится. Так как
расходится. Так как  найдется натуральное k1 та
найдется натуральное k1 та
кое, что при всех k > k1 справедливо  По первому признаку сравнения из
По первому признаку сравнения из  вытекает расходимость ряда
вытекает расходимость ряда  , который представляет собой остаток ряда
, который представляет собой остаток ряда  . Значит,
. Значит,  расходится. ◄
расходится. ◄
Замечание. Доказанная теорема производит сравнение двух рядов по “ско- рости” убывания их общих членов. Если общие члены рядов  и
и  являются бесконечно малыми одинакового порядка (
являются бесконечно малыми одинакового порядка (  , q ≠ 0, +∞ ), то ряды ведут себя одинаково; в частности, ряды ведут себя одинаково, когда их общие члены эквивалентны ( случай q = 1 ). Если общий член ряда
, q ≠ 0, +∞ ), то ряды ведут себя одинаково; в частности, ряды ведут себя одинаково, когда их общие члены эквивалентны ( случай q = 1 ). Если общий член ряда  является бесконечно малой более высокого порядка по сравнению с об- щим членом сходящегося ряда
является бесконечно малой более высокого порядка по сравнению с об- щим членом сходящегося ряда  (ak =o( bk) ), то
(ak =o( bk) ), то  также сходится; если общий член ak убывает “медленнее“ общего члена расходящегося ряда
также сходится; если общий член ak убывает “медленнее“ общего члена расходящегося ряда  , то ряд
, то ряд  также расходится.
также расходится.
Чтобы эффективно применять признаки сравнения, нужно располагать набором рядов, относительно которых уже известно, сходятся они или расходятся, и чем больше различных рядов в этом наборе, тем больше шансов най- ти среди них такой, сравнение с которым позволит выяснить, сходится ли интересующий нас ряд. Мы уже можем включить в этот набор различные ря- ды вида  , где a и q положительные числа – такой ряд сходится, если 0 < q < 1, и расходится, если q ≥ 1 (cм.примеры 1 и 5). В этот набор можем включить также обобщенный гармонический ряд
, где a и q положительные числа – такой ряд сходится, если 0 < q < 1, и расходится, если q ≥ 1 (cм.примеры 1 и 5). В этот набор можем включить также обобщенный гармонический ряд  при всевозможных вещественных λ (пример 6). Вообще, каждый ряд, сходимость которого исследована, пополняет указанный набор рядов.
при всевозможных вещественных λ (пример 6). Вообще, каждый ряд, сходимость которого исследована, пополняет указанный набор рядов.
На второй признак сравнения опирается метод выделения главной части в иследовании рядов на сходимость. Пусть f (x) есть производящая функция ряда  : ak = f (k) . Пусть, далее, С
: ak = f (k) . Пусть, далее, С 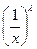 , где С > 0 и λ > 0 , - главная часть f (x) при х → +∞ , т.е. f (x) эквивалентна С
, где С > 0 и λ > 0 , - главная часть f (x) при х → +∞ , т.е. f (x) эквивалентна С 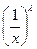 при х → +∞. Из второго признака сравнения следует, что ряд
при х → +∞. Из второго признака сравнения следует, что ряд  ведет себя так же, как ряд
ведет себя так же, как ряд  : он расходится, если λ ≤ 1, и сходится, если λ > 1.
: он расходится, если λ ≤ 1, и сходится, если λ > 1.
Пример 8. Исследуем на сходимость ряд  . Запишем его производящую функцию :
. Запишем его производящую функцию :  . Выделим ее главную часть при х→ +∞ :
. Выделим ее главную часть при х→ +∞ :
 ~
~ 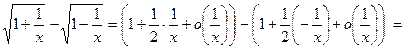
=  ~
~ 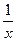 , х→ +∞.
, х→ +∞.
Итак, С = 1 , λ = 1, поэтому рассматриваемый ряд ведет себя так же, как гармонический ряд  , т.е. расходится.
, т.е. расходится.
Теорема 4 .(Признак Даламбера) Пусть {ak} – последовательность положительных чисел, и пусть 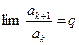 , где q – либо неотрицательное число, либо + ∞. Тогда : 1) если 0≤ q < 1, то ряд
, где q – либо неотрицательное число, либо + ∞. Тогда : 1) если 0≤ q < 1, то ряд  сходится; 2) если q > 1 или q =+ ∞ , то ряд
сходится; 2) если q > 1 или q =+ ∞ , то ряд  расходится.
расходится.
► 1) Пусть р – число, удовлетворяющее неравенствам q < p < 1. По теореме о стабилизации знака неравенства ( [3], п. 3.3 ) найдется натуральное kр такое, что при всех k > kр справедливо  , т.е. аk+1 < p ak. Отсюда при k = kp+1 получим
, т.е. аk+1 < p ak. Отсюда при k = kp+1 получим  при k = kp+2 получим
при k = kp+2 получим  , при k= kp+3 будет
, при k= kp+3 будет  и т.д. Вообще, при всяком натуральном m справедливо неравенство
и т.д. Вообще, при всяком натуральном m справедливо неравенство  . Рассмотрим два ряда :
. Рассмотрим два ряда :  и
и 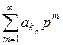 . Для их общих членов справедливо неравенство
. Для их общих членов справедливо неравенство  , причем ряд с бóльшим общим членом сходится, ибо его члены образуют геометрическую прогрессию, знаменатель р которой меньше единицы. По первому признаку сравнения сходится ряд
, причем ряд с бóльшим общим членом сходится, ибо его члены образуют геометрическую прогрессию, знаменатель р которой меньше единицы. По первому признаку сравнения сходится ряд  , который представляет собой остаток ряда
, который представляет собой остаток ряда  ; значит, этот последний ряд сходится.
; значит, этот последний ряд сходится.
2) И в случае q > 1, и в случае q = + ∞ найдется натуральное k0 такое, что при всех k > k0 справедливо  , т.е. начиная с номера k0 члены пос- ледовательности { ak } возрастают, поэтому эта последовотельность не стремится к нулю. Значит, ряд
, т.е. начиная с номера k0 члены пос- ледовательности { ak } возрастают, поэтому эта последовотельность не стремится к нулю. Значит, ряд  расходится. ◄
расходится. ◄
Замечание. В случае q = 1 признак Даламбера не дает ответа на вопрос о сходимости ряда: если 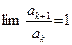 , ряд
, ряд  может оказаться сходящимся , но может окзаться и расходящимся.
может оказаться сходящимся , но может окзаться и расходящимся.
Пример 9. Применим признак Даламбера к ряду  : ak =
: ak =  ,
,
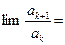
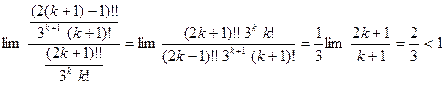 .
.
Значит, ряд сходится.
Теорема 5.( Радикальный признак Коши ) Пусть {ak} – последовательность неотрицательных чисел, и пусть  , где q – либо неотрицательное число, либо +∞. Тогда : 1) если 0 ≤ q < 1, то ряд
, где q – либо неотрицательное число, либо +∞. Тогда : 1) если 0 ≤ q < 1, то ряд  сходится , 2) если q > 1 или q = + ∞, то ряд
сходится , 2) если q > 1 или q = + ∞, то ряд  расходится.
расходится.
► 1) Пусть р – число, удовлетворяющее неравенствам q < р < 1. Най- дется натуральное kр такое, что при всех k > kр справедливо 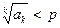 , т.е. ak< <
, т.е. ak< <  . По первому признаку сравнения отсюда следует, что ряд
. По первому признаку сравнения отсюда следует, что ряд 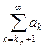 (остаток ряда
(остаток ряда  ) сходится, так как его члены меньше соответствующих членов бесконечно убывающей геометрической прогрессии. Поскольку сходится остаток, то сходится и сам ряд.
) сходится, так как его члены меньше соответствующих членов бесконечно убывающей геометрической прогрессии. Поскольку сходится остаток, то сходится и сам ряд.
2) И в случае q > 1, и в случае q =+ ∞ найдется натуральное k0 такое, что при всех k > k0 справедливо  ; поэтому при указанных k
; поэтому при указанных k  Значит, последовательность {ak} не может стремиться к нулю; ряд
Значит, последовательность {ak} не может стремиться к нулю; ряд  расходится.◄
расходится.◄
Замечание. При q = 1 радикальный признак Коши не не дает ответа на вопрос о сходимости ряда : в этом случае ряд  может оказаться сходящимся, но может и расходиться.
может оказаться сходящимся, но может и расходиться.
Пример 10. Применим радикальный признак Коши к ряду 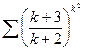 :
:  =
= 
Следовательно, ряд расходится.
4°. Признаки сходимости произвольных рядов
Здесь мы рассматриваем ряды, члены которых могут быть любыми вещественными или мнимыми числами. Начнем с частного, но весьма важного для приложений случая – с рядов, которые принято называть знакочередующимися.
Пусть {ak} – последовательность положительных чисел. Рассмотрим. ряд  . Ряды такой структуры и называют знакочередующимися.
. Ряды такой структуры и называют знакочередующимися.
Теорема 7.( Признак Лейбница ) Пусть последовательность {ak} строго убывает и стремится к нулю. Тогда ряд  сходится; а его сумма S удовлетворяет неравенствам 0 < S ≤ a1.
сходится; а его сумма S удовлетворяет неравенствам 0 < S ≤ a1.
► Пусть n – некоторое четное число: n = 2l , l  N.В сумме S2l сгруппируем слагаемые :
N.В сумме S2l сгруппируем слагаемые :
S2l =  = (а1 –a2) + ( a3 – a4) + … +(a2l-3 –a2l-2 ) + (a2l-1 –a2l )
= (а1 –a2) + ( a3 – a4) + … +(a2l-3 –a2l-2 ) + (a2l-1 –a2l )
Так как {ak} строго убывает,то разность в каждой из скобок положительна; значит, S2l > 0 и S2(l+1) > S2l , т.е. последовательность {S2l } 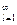 - это строго возрастающая последовательность положительных чисел. Сгруппируем теперь слагаемые в сумме S2l иначе :
- это строго возрастающая последовательность положительных чисел. Сгруппируем теперь слагаемые в сумме S2l иначе :
S2l = a1 – ( a2 –a3 ) – ( a4 –a5 ) - … - ( a2l-2 –a 2l-1 ) – a2l .
Отсюда ясно, что S2l < a1. Таким образом, строго возрастающая последова- тельность { S2l} ограничена сверху числом a1; значит, она сходится. Обозна- чим ее предел через S. Из свойств { S2l } следует: 0 < S ≤ a1
Покажем, что S есть сумма ряда  , т.е., что S = lim Sn , где Sn = =
, т.е., что S = lim Sn , где Sn = =  . Пусть n – некоторое нечетное число: n = 2l –1 , l
. Пусть n – некоторое нечетное число: n = 2l –1 , l  N. Заметим : S2l-1 = = S2l - a2l → S, так как S2l → S, а a2l → 0. Таким образом, обе подпосле- довательности {S2l} частичных сумм с четными номерами и {S2l-1} частичных сумм с нечетными номерами сходятся к S; значит, вся последовательность {Sn}
N. Заметим : S2l-1 = = S2l - a2l → S, так как S2l → S, а a2l → 0. Таким образом, обе подпосле- довательности {S2l} частичных сумм с четными номерами и {S2l-1} частичных сумм с нечетными номерами сходятся к S; значит, вся последовательность {Sn}  имеет тот же предел
имеет тот же предел
Итак, ряд сходится, а его сумма S удовлетворяет неравенствам 0< S ≤ a1. ◄
Пример 10. Рассмотрим ряд  , где λ – некоторое вещественное число. Это знакочередующийся ряд; здесь ak =
, где λ – некоторое вещественное число. Это знакочередующийся ряд; здесь ak = 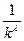 . Если λ ≤0 , последователь- ность {ak}, очевидно, не стремится к нулю, и поэтому при таких λ ряд расхо- дится. При λ > 0 последовательность {ak} строго убывает и стремится к ну- лю; значит, по признаку Лейбница ряд сходится.
. Если λ ≤0 , последователь- ность {ak}, очевидно, не стремится к нулю, и поэтому при таких λ ряд расхо- дится. При λ > 0 последовательность {ak} строго убывает и стремится к ну- лю; значит, по признаку Лейбница ряд сходится.
В следующей теореме члены ряда  - любые числа, быть может, мнимые. Из их модулей составим новый ряд
- любые числа, быть может, мнимые. Из их модулей составим новый ряд  ; члены этого ряда неотрицательны.
; члены этого ряда неотрицательны.
Теорема 8.Если сходится ряд  , то сходится и ряд
, то сходится и ряд  .
.
► Зададим некоторое ε > 0. Так как  сходится, в силу критерия Коши (свойство 1, 2˚ ) существует натуральное nε такое, что при всех n > nε и любых натуральных р справедливо
сходится, в силу критерия Коши (свойство 1, 2˚ ) существует натуральное nε такое, что при всех n > nε и любых натуральных р справедливо  . Ho при этих n и p
. Ho при этих n и p 
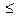
 , т.е., для ряда
, т.е., для ряда  выполнены требования критерия Коши:
выполнены требования критерия Коши:
 N
N 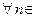 N
N  N ( n > nε
N ( n > nε 

 ) ,
) ,
поэтому ряд  сходится . ◄
сходится . ◄
Пример 11. Рассмотрим ряд  , где φ и λ – вещественные числа. Так как │exp(ikφ)│= 1, то
, где φ и λ – вещественные числа. Так как │exp(ikφ)│= 1, то 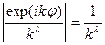 . Отсюда ясно, что при λ ≤ 0 общий член рассматриваемого ряда не стремится к нулю, поэтому ряд расходится, а при λ > 1 ряд
. Отсюда ясно, что при λ ≤ 0 общий член рассматриваемого ряда не стремится к нулю, поэтому ряд расходится, а при λ > 1 ряд  сходится ( см. пример 6), значит, сходится и рассматриваемый ряд. Его поведение при
сходится ( см. пример 6), значит, сходится и рассматриваемый ряд. Его поведение при  будет выяснено ниже с помощью признака Дирихле.
будет выяснено ниже с помощью признака Дирихле.
Лемма Абеля.Пусть  и
и  - наборы комплексных чисел Обозначим: Vq=
- наборы комплексных чисел Обозначим: Vq= 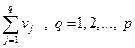 ; V = max { |V1| , |V2| , … , |Vp| } . Тогда :
; V = max { |V1| , |V2| , … , |Vp| } . Тогда :
1) 
2)2) если u1 ≥ u2 ≥ … ≥ up > 0 , то  .
.
► Заметим : V1 = v1, а при j = 2,3, …, p vj = Vj – Vj-1. Значит,

Раскрыв здесь скобки и приведя затем подобные, получим равенство 1).
 ◄
◄
Теорема 9.( Признак Дирихле ) Пусть  - монотонная невозрастающая последовательность положительных чисел, а
- монотонная невозрастающая последовательность положительных чисел, а  - последовательность комплексных чисел. Обозначим: Вр =
- последовательность комплексных чисел. Обозначим: Вр = 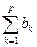 . Если 1)
. Если 1)  и 2) существует М > 0 такое, что
и 2) существует М > 0 такое, что  М при всех р
М при всех р  N, то ряд
N, то ряд  сходится.
сходится.
► Покажем, что ряд  удовлетворяет требованиям критерия Коши
удовлетворяет требованиям критерия Коши  N
N  N
N  N( n > nε
N( n > nε  )
)
Зададим ε > 0. По условию 1)  , значит, найдется натуральное n ε такое, что из k > n ε следует
, значит, найдется натуральное n ε такое, что из k > n ε следует  . Пусть n и р – натуральные числа, причем n > n ε. Имеем:
. Пусть n и р – натуральные числа, причем n > n ε. Имеем:  , где u j = an+j , v j = b n+j . Заметим: u1 ≥ u2 ≥ … ≥ up > 0 . Обозначим: Vq =
, где u j = an+j , v j = b n+j . Заметим: u1 ≥ u2 ≥ … ≥ up > 0 . Обозначим: Vq =  , V = max { |V1| , |V2| , … , |Vp| }. Так как Vq =
, V = max { |V1| , |V2| , … , |Vp| }. Так как Vq =  = Bn+q – Bq, то при любом натуральном q имеем : | Vq | ≤ ≤ | Bn+q| + |Bq| ≤ 2M . Значит, V ≤ 2M . В силу утверждения 2) леммы Абеля
= Bn+q – Bq, то при любом натуральном q имеем : | Vq | ≤ ≤ | Bn+q| + |Bq| ≤ 2M . Значит, V ≤ 2M . В силу утверждения 2) леммы Абеля  , т.е. |
, т.е. |  | ≤ 2М an+1. Отсюда и из неравенствa
| ≤ 2М an+1. Отсюда и из неравенствa 
 следует : |
следует : |  | < ε . Таким образом, для произвольно заданного ε>0 существует натуральное n ε , удовлетворяющее требованию критерия Коши ; поэтому ряд сходится. ◄
| < ε . Таким образом, для произвольно заданного ε>0 существует натуральное n ε , удовлетворяющее требованию критерия Коши ; поэтому ряд сходится. ◄
Пример 12. Вернемся к рассмотрению ряда  . Пусть 0 < λ ≤ 1. Ввиду 2π – периодичности exp(ikφ), достаточно рассматривать
. Пусть 0 < λ ≤ 1. Ввиду 2π – периодичности exp(ikφ), достаточно рассматривать  . Если φ = 0, ряд превращается в
. Если φ = 0, ряд превращается в  , который при 0 < λ ≤ 1 расходится ( пример 6). Пусть φ
, который при 0 < λ ≤ 1 расходится ( пример 6). Пусть φ 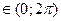 . При всяком k
. При всяком k  Nположим
Nположим 
 где q
где q  . Заметим: при 0 < λ ≤ 1 последовательность
. Заметим: при 0 < λ ≤ 1 последовательность  убывает и стремится к нулю; далее, при φ
убывает и стремится к нулю; далее, при φ 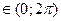 q отлично от единицы, поэтому Bp =
q отлично от единицы, поэтому Bp = 
 , и, значит, |Bp|
, и, значит, |Bp| 
 , где М от р не зависит. Таким образом, последовательности
, где М от р не зависит. Таким образом, последовательности  и
и  удовлетворяют требованиям признака Дирихле, значит, ряд
удовлетворяют требованиям признака Дирихле, значит, ряд  , т.е.
, т.е.  при 0 < λ ≤ 1 и φ
при 0 < λ ≤ 1 и φ 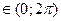 сходится.
сходится.
Теорема 10.( Признак Абеля) Пусть  - невозрастающая последова- тельность положительных чисел, а
- невозрастающая последова- тельность положительных чисел, а  - последовательность комплексных чисел. Если сходится ряд
- последовательность комплексных чисел. Если сходится ряд  , то сходится и ряд
, то сходится и ряд  .
.
► Обозначим:  . Заметим: {ck} – невозрастающая бесконечно малая последовательность положительных чисел; {Bp} – последовательность частичных сумм сходящегося ряда, значит, это сходя- щаяся и потому ограниченная последовательность. По признаку Дирихле ряд
. Заметим: {ck} – невозрастающая бесконечно малая последовательность положительных чисел; {Bp} – последовательность частичных сумм сходящегося ряда, значит, это сходя- щаяся и потому ограниченная последовательность. По признаку Дирихле ряд  , т.е.
, т.е.  сходится. Но
сходится. Но  , а это означает, что ряд
, а это означает, что ряд  является суммой двух сходящихся рядов
является суммой двух сходящихся рядов  и
и  . Следовательно ( свойство 5, 2˚ ), ряд
. Следовательно ( свойство 5, 2˚ ), ряд  сходится. ◄
сходится. ◄
5 ˚. Абсолютно сходящиеся ряды
Если сходится ряд  , то ряд
, то ряд  также сходится ( теорема 8 ). Если же
также сходится ( теорема 8 ). Если же  расходится, то
расходится, то  может оказаться как сходящимся, так и расхо- дящимся рядом. Ряд
может оказаться как сходящимся, так и расхо- дящимся рядом. Ряд  называют абсолютно сходящимся рядом, если сходится
называют абсолютно сходящимся рядом, если сходится  . Если
. Если  сходится, а
сходится, а  расходится, то говорят, что
расходится, то говорят, что  сходится неабсолютно или условно.
сходится неабсолютно или условно.
Пример 13. При λ ≤ 0 ряд  расходится, а при λ > 0 он сходится ( пример 10) . Заметим:
расходится, а при λ > 0 он сходится ( пример 10) . Заметим:  , а
, а  расходится при 0 < λ ≤ 1 и сходится при λ > 1. Значит, при 0 < λ ≤ 1 ряд
расходится при 0 < λ ≤ 1 и сходится при λ > 1. Значит, при 0 < λ ≤ 1 ряд  сходится условно, а при λ > 1 его сходимость абсолютная.
сходится условно, а при λ > 1 его сходимость абсолютная.
Пример 14. Пусть φ 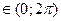 . Ряд
. Ряд  сходится при λ > 0 ( при- меры 11 и 12). Так как
сходится при λ > 0 ( при- меры 11 и 12). Так как 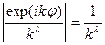 , то при 0 < λ ≤ 1 сходимость этого ряда условная, а при λ > 1 - абсолютная.
, то при 0 < λ ≤ 1 сходимость этого ряда условная, а при λ > 1 - абсолютная.
Абсолютно сходящиеся ряды представляют особый интерес, ибо они обладают свойствами, сближающими их с конечными суммами. Ниже эти свойства будут рассмотрены подробно; а пока отметим, что их наличие упрощает обращение с абсолютно сходящимися рядами; поэтому, имея дело со сходящимся рядом  , важно выяснить, является ли он абсолютно схо- дящимся, для чего нужно исследовать сходимость ряда
, важно выяснить, является ли он абсолютно схо- дящимся, для чего нужно исследовать сходимость ряда  . Так как члены его неотрицательны, применимы теоремы, изложенные в 3˚. Кроме того, если z k- мнимые числа, часто оказывается полезной следующая теорема.
. Так как члены его неотрицательны, применимы теоремы, изложенные в 3˚. Кроме того, если z k- мнимые числа, часто оказывается полезной следующая теорема.
Теорема 11 .Пусть  и
и 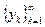 - последовательности вещественных чисел . Обозначим : zk = xk + i yk. Для того чтобы ряд
- последовательности вещественных чисел . Обозначим : zk = xk + i yk. Для того чтобы ряд  абсолютно сходился, необходимо и достаточно, чтобы абсолютно сходились оба ряда
абсолютно сходился, необходимо и достаточно, чтобы абсолютно сходились оба ряда  и
и 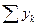 .
.
► Необходимость. Так как |x k| ≤ |z k|, то в силу первого признака сравнения из сходимости  вытекает сходимость
вытекает сходимость  . Доказательство схо- димости
. Доказательство схо- димости  аналогично.
аналогично.
Достаточность. Пусть  и
и  сходятся; тогда сходится и
сходятся; тогда сходится и  . Из неравенства |z k| ≤ |x k| + |yk| и первого признака сравне- ния вытекает сходимость
. Из неравенства |z k| ≤ |x k| + |yk| и первого признака сравне- ния вытекает сходимость  . ◄
. ◄
Пример 15. Рассмотрим ряды  и
и