 |
|
Знакочередующиеся ряды
Ряд вида  , где
, где  (5) называется знакочередующимся рядом.
(5) называется знакочередующимся рядом.
Признак Лейбница. Если члены ряда (5) по модулю монотонно убывают с ростом  , то есть
, то есть  , начиная с некоторого n и
, начиная с некоторого n и  , то ряд (5) сходится . Если нарушено хотя бы одно из указанных условий, то ряд расходится.
, то ряд (5) сходится . Если нарушено хотя бы одно из указанных условий, то ряд расходится.
Пример. Даны числовые ряды:
А) 
В) 
Выяснить характер сходимости этих рядов. Ответ. А сходится, В расходится.
Решение. Для ряда А модулем общего члена ряда является 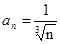 . Ясно, что он монотонно уменьшается , начиная с n=1,
. Ясно, что он монотонно уменьшается , начиная с n=1,  . Условия признака Лейбница выполнены, следовательно ряд А сходится.
. Условия признака Лейбница выполнены, следовательно ряд А сходится.
Для ряда В модулем общего члена ряда является 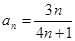 . Очевидно, что второе условие признака Лейбница не выполнено, так как
. Очевидно, что второе условие признака Лейбница не выполнено, так как  , следовательно ряд В расходится.
, следовательно ряд В расходится.
Определение. Знакочередующийся ряд сходится абсолютно, если сходится ряд составленный из абсолютных значений его членов, то есть если сходится ряд  .
.
Утверждение. Если знакочередующийся ряд сходится абсолютно, то он просто сходится, то есть справедлива схема:
 -сходится
-сходится 
 - сходится
- сходится
Определение. Если ряд  сходится, а ряд
сходится, а ряд  расходится ( расходится абсолютно), то говорят, что ряд
расходится ( расходится абсолютно), то говорят, что ряд  сходится условно.
сходится условно.
Пример. Укажите правильное утверждение относительно сходимости знакочередующихся рядов:
А)  и В)
и В)  . Ответ. А расходится, В сходится условно.
. Ответ. А расходится, В сходится условно.
Обоснование.  , то есть нарушено второе условие признака Лейбница, следовательно ряд А расходится. Относительно ряда В). Так как коэффициенты
, то есть нарушено второе условие признака Лейбница, следовательно ряд А расходится. Относительно ряда В). Так как коэффициенты  убывают монотонно с ростом
убывают монотонно с ростом  и
и  , то есть выполнены оба условия признака Лейбница, ряд В) сходится. Но ряд
, то есть выполнены оба условия признака Лейбница, ряд В) сходится. Но ряд 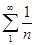 расходится, следовательно ряд В) сходится условно.
расходится, следовательно ряд В) сходится условно.
Степенные ряды
Ряд вида  называется
называется
степенным рядом. Здесь  - коэффициенты ряда (действительные числа),
- коэффициенты ряда (действительные числа), 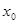 - центр ряда.
- центр ряда.
Существует положительное число 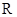 такое , что степенной ряд сходится при всех
такое , что степенной ряд сходится при всех  из интервала
из интервала  и расходится при всех
и расходится при всех  , лежащих вне этого интервала.
, лежащих вне этого интервала.
Такое  называется радиусом сходимости степенного ряда, а интервал
называется радиусом сходимости степенного ряда, а интервал 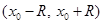 - интервалом или областью сходимости.
- интервалом или областью сходимости.
Радиус сходимости можно найти по формулам
 или
или 
Пример. Найти область сходимости степенного ряда  и исследовать сходимость на границе этой области.
и исследовать сходимость на границе этой области.
Решение. Здесь  . Радиус сходимости
. Радиус сходимости 
 . Центр ряда
. Центр ряда  , интервал или область сходимости
, интервал или область сходимости  . На левом конце при
. На левом конце при  получим
получим
числовой ряд  который расходится, так как
который расходится, так как  . На правом конце при
. На правом конце при  получим числовой ряд
получим числовой ряд
 , который расходится, так как
, который расходится, так как  . Таким образом областью сходимости степенного ряда является интервал
. Таким образом областью сходимости степенного ряда является интервал 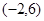 .
.