 |
|
Признаки сходимости рядов с положительными членами
Основной вопрос, на который надо ответить при исследовании данного ряда ─ сходится он или нет. И если да, то по возможности найти его сумму. Как мы видели, полный ответ был получен для суммы бесконечно убывающей геометрической прогрессии. Но это скорее исключение. Сходимость ряда устанавливают с помощью так называемых признаков сходимости . Мы начнем с рядов с положительными членами и приведем для них основные признаки сходимости.
Итак, будем рассматривать ряды  с
с  . ( Заметим, что если члены ряда неотрицательны, то все нулевые слагаемые можно отбросить и ряд перенумеровать, тогда получим ряд с положительными членами).
. ( Заметим, что если члены ряда неотрицательны, то все нулевые слагаемые можно отбросить и ряд перенумеровать, тогда получим ряд с положительными членами).
Частичные суммы такого ряда положительны и возрастают. Поэтому, исходя из признака существования предела последовательности, можно сразу сформулировать достаточный признак ряда сходимости ряда с положительными членами.
Если частичные суммы  ограничены, т.е. существует такое
ограничены, т.е. существует такое  что для всех
что для всех 
 , то последовательность частичных сумм имеет предел, т.е. ряд сходится.
, то последовательность частичных сумм имеет предел, т.е. ряд сходится.
Пользоваться этим признаком затруднительно, его мы используем для доказательства других достаточных признаков.
I. Признак сравнения в форме неравенства.
Теорема 1.Пусть даны два ряда
(А)  и
и
(В)  .
.
Если начиная с некоторого номера  выполняется неравенство
выполняется неравенство
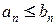 ,
,
то из сходимости ряда (В) следует сходимость ряда (А), из расходимости ряда (А) следует расходимость ряда (В).
Доказательство.
Не ограничивая общности можно считать 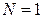 (почему?).
(почему?).
Обозначим частичные суммы ряда (А) 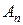 , а ряда (В) ─
, а ряда (В) ─  . Тогда в силу условия верно неравенство
. Тогда в силу условия верно неравенство  .
.
Пусть ряд (В) сходится. Значит, существует 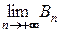
 величины
величины  ограничены
ограничены 
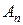 ограничены
ограничены  существует
существует 
 ряд (А) сходится.
ряд (А) сходится.
Пусть теперь ряд (А) расходится. Тогда 
 также не может иметь конечный предел. ■
также не может иметь конечный предел. ■
Замечание. Часто ряд (В) называют мажорантой ряда (А), тогда говорят, что из сходимости мажоранты следует сходимость ряда. Реже ряд (А) называют минорантой ряда (В).
Чтобы использовать признак сравнения для исследования сходимости данного ряда следует найти либо сходящуюся мажоранту либо расходящуюся миноранту.
Примеры.
1.  .
.
Верно неравенство  . Ряд
. Ряд  сходится как сумма бесконечно убывающей геометрической прогрессии, значит, сходится и ряд
сходится как сумма бесконечно убывающей геометрической прогрессии, значит, сходится и ряд  .
.
2.  . Очевидно, что при
. Очевидно, что при  этот ряд расходится. Поэтому рассмотрим два следующих случая.
этот ряд расходится. Поэтому рассмотрим два следующих случая.
а).  . Верно, что
. Верно, что  . Известно, что гармонический ряд
. Известно, что гармонический ряд  расходится,
расходится,  расходится ряд
расходится ряд  при
при  .
.
б).  . Запишем
. Запишем  в виде
в виде  . Возьмем вспомогательный ряд
. Возьмем вспомогательный ряд  . Найдем частичные суммы этого ряда
. Найдем частичные суммы этого ряда 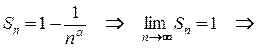 этот ряд сходится. Теперь к функции
этот ряд сходится. Теперь к функции  применим теорему Лагранжа на отрезке
применим теорему Лагранжа на отрезке  , получим
, получим
 , где точка
, где точка  расположена между
расположена между  и
и  , поэтому
, поэтому  .
.
Итак, для некоторого 
 верно равенство
верно равенство  .
.
Так как  , то
, то 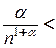
 .
.
Таким образом, сходящийся ряд  является мажорантой ряда
является мажорантой ряда 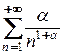
 ряд
ряд 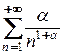 сходится
сходится  ряд
ряд  при
при  сходится.
сходится.
Приведенные примеры показывают, что необходимо иметь набор эталонных рядов, сходящихся и расходящихся, с которыми следует сравнить исследуемый ряд.
Эталонные ряды.
| Сходящиеся ряды | Расходящиеся ряды |
 при при 
|  при при 
|
 при при  , , 
|  при при 
|