 |
|
Сходимость знакопеременных рядов
10. Будем рассматривать ряд
(А)  ,
,
члены которого могут быть как положительными, так и отрицательными. Наряду с рядом (А) рассмотрим ряд с неотрицательными членами
(А*)  .
.
Теорема 1 .
Если ряд (А*) сходится, то сходится и ряд (А).
Доказательство.
Построим два вспомогательных положительных ряда
(Р) 
(Q) 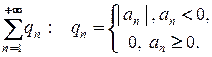
Каждый из рядов (Р) и (Q) сходится, т.к. их частичные суммы не превышают частичных сумм ряда (А*), значит, они ограничены, и ряды сходятся по достаточному признаку сходимости положительных рядов. Нетрудно видеть, что
 =
= 
 .
.
Поэтому ряд (А) как разность двух сходящихся рядов сходится. ■
Определение. Ряд (А) называется абсолютно сходящимся, если сходится ряд (А*). Если же ряд (А*) расходится, а ряд (А) сходится, то он называется условно сходящимся.
20. Знакочередующиеся ряды.
Определение. Ряд
(С)  , где все
, где все 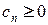 называется знакочередующимся.
называется знакочередующимся.
Теорема 2.(Признак Лейбница)
Пусть для ряда (С) выполнены условия:
1. 
2. 
3. 
Тогда ряд (С) сходится.
Доказательство.
Сначала рассмотрим поведение частичных сумм ряда (С) с четными номерами

Так как  ,
,  , то выражения во всех скобках положительны, и поэтому
, то выражения во всех скобках положительны, и поэтому  и
и  возрастают. С другой стороны,
возрастают. С другой стороны,
 , что означает ограниченность
, что означает ограниченность  .
.
Итак, частичные суммы с четными номерами возрастают и ограничены сверху 
 .
.
Частичные суммы с нечетными номерами  и при
и при  , поэтому
, поэтому  . ■
. ■
Примеры.
1) Рассмотрим знакопеременный ряд  . Верно неравенство
. Верно неравенство  .
.
Так как ряд  сходится, то сходится ряд
сходится, то сходится ряд 
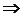 ряд
ряд  сходится абсолютно.
сходится абсолютно.
2). Знакочередующийся ряд  очевидно удовлетворяет условиям признака Лейбница
очевидно удовлетворяет условиям признака Лейбница 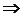 он сходится. С другой стороны, ряд из модулей
он сходится. С другой стороны, ряд из модулей  расходится
расходится 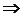 ряд
ряд  сходится условно.
сходится условно.
Введем понятие скорости сходимости сходящегося ряда. Пусть  . Для любого остатка
. Для любого остатка  можно записать
можно записать  . Как было показано,
. Как было показано,  , т.е.
, т.е.  является бесконечно малой при
является бесконечно малой при  . Порядок малости назовем скоростью сходимости ряда. Рассмотрим сумму бесконечно убывающей прогрессии
. Порядок малости назовем скоростью сходимости ряда. Рассмотрим сумму бесконечно убывающей прогрессии  . Остаток
. Остаток 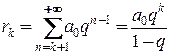 . Говорят, что скорость сходимости соответствует
. Говорят, что скорость сходимости соответствует  .
.
Любой сходящийся знакочередующийся ряд, удовлетворяющий признаку Лейбница, также позволяет узнать скорость его сходимости.
Имеем 
Теорема 3. (Оценка остатка знакочередующегося ряда)
Модуль остатка знакочередующегося ряда не превышает модуля первого отброшенного члена,  и имеет его знак, т.е. знак
и имеет его знак, т.е. знак  .
.
Доказательство.
Рассмотрим сначала остаток с номером 
 . Теперь вспомним доказательство признака Лейбница ─ частичные суммы с четными номерами больше 0 и меньше первого члена, более того, сумма ряда также больше 0 и меньше первого члена . Значит,
. Теперь вспомним доказательство признака Лейбница ─ частичные суммы с четными номерами больше 0 и меньше первого члена, более того, сумма ряда также больше 0 и меньше первого члена . Значит, 
Пусть теперь 
 или
или

Ясно, что  и
и  отрицателен. ■
отрицателен. ■