 |
|
Th 3. Критерий сходимости Коши
Числовые ряды
Понятие числового ряда
Пусть дана произвольная числовая последовательность
(1)
Образуем суммы
, 
, ... , 
, ...
и составим из них новую последовательность
(2)
Предположим, что предел последовательности (2) при 
существует, конечен и равен 
. Тогда называют суммой числового ряда
(3)
который кратко обозначают:
(4)
Члены последовательности (1) называются членами ряда (3), а члены последовательности (2) – частичными суммами ряда.
Если предел частичных сумм ряда (4) существует, конечен и равен S, то ряд (4) называется сходящимся к числу S или просто сходящимся, а число S – суммой ряда. При этом пишут: 
.
I Пусть дан ряд 
или 
. Его члены образуют геометрическую прогрессию со знаменателем 
и первым членом 
. Из курса математики известно, что
ее сумма равна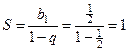 
.
I Рассмотрим ряд 
.
Итак, ряд сходится к единице.
Если последовательность частичных сумм (2) ряда (4) не имеет конечного предела, то ряд называется расходящимся, в этом случае считается, что ряд не имеет суммы.
I Рассмотрим ряд 
.
- не существует, следовательно, ряд расходящийся, не имеющий суммы.
Простейшие свойства сходящихся рядов
Th 1. Необходимый признак сходимости ряда
Если ряд (4) сходится, то 
.
□
Пусть 
n-ая частичная сумма ряда (4). Если ряд (4) сходится, то по определению существует конечный предел (3), но тогда существует и 
, тогда
.
■
Следствие. Достаточный признак расходимости ряда.
Если общий член ряда (4) не стремится к нулю, то ряд (4) расходится.
Замечание. Условие стремления к нулю общего члена ряда является лишь необходимым признаком, но не является достаточным.
I Рассмотрим ряд 
.
Поэтому 
- ряд расходится, однако 
.
Th 2.
Пусть ряд
(5)
получен из ряда (4) отбрасыванием конечного числа членов. Тогда ряды (4) и (5) сходятся или расходятся одновременно.
□
Пусть ряд (5) получен из (4) отбрасыванием каких то k членов сумма которых равна A. Пусть и 
- частичные суммы рядов (4) и (5) соответственно. Пусть 
- номер последнего из отброшенных членов. Очевидно, что для любого 
, тогда если существует конечный предел , то существует и конечный предел . И наоборот, если конечного предела не существует, то ряд (5) расходится. Следовательно, ряды (4) и (5) сходятся и расходятся одновременно.
■
Th 3. Критерий сходимости Коши
Для того, чтобы ряд (4) сходился необходимо и достаточно, чтобы
. (6)
□
Пусть - n-ая частичная сумма ряда (4). Ряд (4) сходится тогда и только тогда, когда имеется конечный предел последовательности частичных сумм (2), а эта последовательность по критерию Коши для предела последовательностей имеет конечный предел тогда и только тогда, когда выполняется условие (6).
■
Th 4.
Если ряд (4) сходится к числу S, то ряд 
, где 
сходится к 
.
□
■
Th 5.
Если ряды (4) и (5) сходятся к S и 
соответственно, то ряд 
сходится к 
.
□
■