Главная | Обратная связь

Th Лейбница. Достаточный признак сходимости знакочередующегося ряда.

Пусть ряд (1) таков, что

(2)

и , (3)

тогда ряд (1) сходится, а его сумма S удовлетворяет неравенству

. (4)

□

Рассмотрим сумму 2m первых членов ряда (1) записывая ее в следующих двух видах:

(5)

и (6)

В силу соотношений (2) и (5) величина S_2m является неубывающей, а в силу (2) и (6) она ограничена сверху числом c₁, следовательно, конечный предел , удовлетворяющий неравенствам (4).

В силу неравенства (3):

, следовательно, и выполняется (4).

■

Замечание 1. Остаток знакочередующегося ряда (1) после nего членов сам является знакочередующимся рядом, удовлетворяющим тем же условиям (2) и (3), следовательно, его сумма 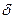удовлетворяет неравенству 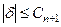. Отсюда, в частности, вытекает, что отбрасывание остатка в знакочередующихся рядах приводит к погрешности в вычислении суммы, не превышающей первого из отброшенных членов.

I Ряд - сходится по теореме Лейбница, его сумма приближенно равна

с погрешностью .

Знакопеременные ряды

Числовой ряд (1) называется знакопеременным, если среди его членов содержатся как положительные, так и отрицательные числа.

Th 1. Достаточный признак сходимости знакопеременного ряда.

Пусть знакопеременный ряд (1) таков, что ряд

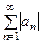(2)

сходится, тогда и ряд (1) тоже сходится.

□

Пусть и - n-ые частичные суммы рядов (1) и (2) соответственно. Пусть и соответственно сумма положительных членов и сумма абсолютных величин отрицательных членов, среди первых n членов ряда (1). Тогда

(3)

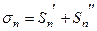и (4).

Предположим, что ряд (2) сходится, следовательно, его частичные суммы стремятся к некоторому конечному пределу , причем 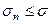, т.е. и .

Мы видим, что последовательности { } и { } являются неубывающими и ограниченными сверху. Поэтому эти последовательности имеют конечные пределы и соответственно.

Тогда в силу равенства (3) существует и конечный предел последовательности { } и он равен - , а это говорит о сходимости ряда (1).

■

Замечание.

Если ряд (2) сходится, то ряд (1) называют абсолютно сходящимся.

Если ряд (2) расходится, а ряд (1) сходится, то ряд (1) называется условно сходящимся.

Возможны следующие случаи

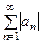
		Название
сходится	сходится	абс. сходящийся
сходится	расходится	усл. сходящийся
расходится	расходится	расходящийся