 |
|
Пункт 4. Достаточные признаки сходимости знакоположительных рядов
ТЕОРИЯ РЯДОВ
Числовые ряды
Пункт 1. Введение
Теория рядов по отношению к основным понятиям и законам математического анализа играет роль вспомогательного аппарата (имеет техническое значение). Но среди методов современной математики занимает центральное место ввиду многочисленных и разнообразных применений в математике и прикладных науках.
Пусть дана числовая последовательность u1, u2,u3, … , un, …
Бесконечным рядомназывается составленный из этих чисел символ.
u1 +u2+u3+ … +un+ … (1)
или 
u1, u2, …члены ряда; un – общий член ряда
Частичными суммами ряда (1) назовем следующие суммы членов ряда:
s1=u1
s2=u1+u2
s3=u1+u2+u3
…
sn= u1+u2+u3 +…+un
…
Таким образом, мы построили последовательность частичных сумм:
s1, s2, s3, … , sn, …
Определение: Ряд (1) называется сходящимся, если существует конечный предел последовательности частичных сумм.


При этом число S называется суммой ряда.
Ряд (1) называется расходящимся в противном случае (у него суммы нет).
Понятие суммы ряда, следовательно, строится не в точности подобно конечных суммам. Здесь участвует новая операция – предельный переход.
Поэтому свойства конечных сумм переносить на ряды без специальной проверки нельзя.
Итак, вопрос сходимости ряда сводится к вопросу существования предела последовательности его частичных сумм, т.е. любая задача теории рядов может быть сформулирована в терминах последовательности и обратно  .
.
Обратно. Если дана последовательность x1, x2, … , xn, … то вопрос о его сходимости может быть сведен к вопросу о сходимости вот такого ряда:
x1+(x2-x1)+(x3-x2)+…+(xn-xn-1)+…
Для такого ряда данная последовательность является последовательностью его частичных сумм. Таким образом, изучение ряда и его суммы есть новая форма изучения понятия последовательности и ее предела. Но эта форма имеет большие преимущества при установлении существования предела и при его вычислении.
Пример 1. Рассмотрим ряд, который называется геометрической прогрессией.
a+aq+aq2+…+aqn-1+… q – знаменатель прогрессии.
Известно, что sn (общий член последовательности частичных сумм) имеет вид:


Ряд сходится при |q|<1 и расходится при |q|  1
1
(при q=1, получается a+a+a+…+a= sn=na  ∞ при
∞ при  )
)
Остатком ряда после m члена называется ряд um+1+um+2+…+um+k+… . Если он сходится, то его сумму будем обозначать rm.
Пример 2. Найти сумму ряда 
1. Построим последовательность частичных сумм
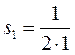



…………
sn= 
………..
2.

Пример 3. (см. уч. стр. 44)
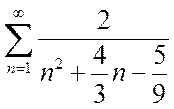
1.

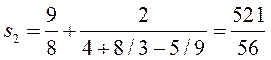
Процесс построения частичных сумм малоприятен и вряд ли приведет к результату. Вернемся к примеру 2 и решим его иначе:



…………..
 , при n →∞
, при n →∞
).
Вернемся к задаче из примера №3.
Un= 
1.
Решим квадратное уравнение  =0, найдем его корни n1=1/3, n2=-5/3
=0, найдем его корни n1=1/3, n2=-5/3
Значит ,наше уравнение эквивалентно уравнению:(n-1/3)(n+5/3)=0

2. Найдем A и B
2=A(n+5/3)+B(n-1/3)
Положим n=1/3, тогда А=1; n=-5/3, В= -1
Получаем Un = 





…………………………….

…….
ПЕРЕЙДЕМ К ПРЕДЕЛУ при n →∞ И ПОЛУЧИМ,ЧТО
s= 
Выполнить задачу №1 в своем варианте контрольной работе №9 стр 183.
Пункт 2. Общие свойства рядов
---
Позже мы будем общее понятие ряда конкретизировать, выделяя специальные классы рядов. Свойства, приведенные в этом пункте являются общими для всех видов рядов.
1 Отбрасывание конечного числа начальных членов ряда или присоединение в начале конечного числа членов не отражается на сходимости ряда
Доказательство:
Пусть дан ряд u1 +u2+u3+ … + um + um+1+um+2+…+um+k+… (1)
Отбросим m членов: um + um+1+um+2+…+um+k+… (2)
Пусть ряд (1) сходится, покажем сходимость ряда (2):
 - общий член последовательности сумм ряда (2).
- общий член последовательности сумм ряда (2).

Следовательно ряд (2) сходится.
Попутно мы установили полезное соотношение 
Пуст теперь сходится ряд (2), покажем сходимость ряда (1).

Утверждение доказательства о расхождении очевидны.
1 Отбрасывание конечного числа начальных членов ряда или присоединение в начале конечного числа членов не отражается на сходимости ряда
2 Сумма остатка сходящегося ряда есть величина бесконечно малая
Имеем

3 Принцип сходимости:
Для сходимости ряда, т.е. для сходимости последовательности его частичных сумм необходимо и достаточно выполнение условия Коши:

Это условие можно переписать в иной форме:

По выражению русского математика Хинчина:
Для сходимости ряда необходимо и достаточно, чтобы всякий достаточно удаленный кусок ряда любой длины по модулю был сколько угодно мал.
Без доказательства.
Практическое применение этого принципа затруднительно, поэтому в теории устанавливаются различные признаки сходимости. Они не так универсальны, но практически удобны.
4. Необходимый признак сходимости
Если ряд (1) сходится, то необходимо 
(или, что то же самое: условие 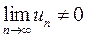 является достаточным для расходимости ряда).
является достаточным для расходимости ряда).
Доказательство: un=sn-sn-1

Отметим, что это условие не является достаточным для сходимости ряда.
Пример:
 , такой ряд называется гармоническим – каждый член этого ряда является средним гармоническим предыдущего и последующего чисел (
, такой ряд называется гармоническим – каждый член этого ряда является средним гармоническим предыдущего и последующего чисел (  ).
).  , но расходится.
, но расходится.
Рассмотрим гармонический ряд. Отбросим первые 2k членов. Получим:

Рассмотрим:

Здесь все слагаемые больше последнего
 , таким образом, при любом условии принципа сходимости не выполнена. Кусок ряда >1/2, n=2k, p=2k.
, таким образом, при любом условии принципа сходимости не выполнена. Кусок ряда >1/2, n=2k, p=2k.
5 Почленное сложение двух сходящихся рядов дает ряд, сумма которого равна сумме сумм слагаемых рядов.
6 Умножение всех членов сходящегося ряда на число приводит к сходящемуся ряду, сумма которого равна произведению суммы этого ряда на это число.
Упражнения на дом
Пункт 3. Знакопостоянные ряды
Будем рассматривать ряды, обладающие некоторыми специальными свойствами, но наиболее доступные для исследования. Среди них важнейший класс – класс знакопостоянных рядов, т.е. рядов, члены которых либо положительны, либо отрицательны.
Будем считать для определенности, что все знаки положительны, вернее не отрицательны. Ряды с отрицательными членами по симметрии будут обладать аналогичными свойствами.
Пусть ряд: u1 +u2+u3+ … +un+ …, все ui ≥0
Очевидно, что последовательность частичных сумм s1, s2, s3, … , sn, … монотонно не убывает. Если она не ограниченна, то sn →∞ , и ряд расходится. Если она ограниченна, то sn →S, и ряд сходится.
Таким образом, условие сходимости знакопостоянного ряда ограниченность последовательности его частичных сумм. Этот факт чрезвычайно важен, т.к. выражение для sn часто бывает сложным для непосредственного вычисления предела. Отмеченный же факт говорит о том, что достаточно установить ограниченность последовательности s1, s2, s3, … , sn. На этом предположении основаны все признаки сходимости знакоположительных рядов.
Пункт 4. Достаточные признаки сходимости знакоположительных рядов
Ограничимся рассмотрением следующих признаков рядов:
1. Признак сравнения рядов
2. Признак Д’Аламбера
3. Признак Коши
4. Интегральный признак сходимости
I .Признак сравнения
Пусть даны 2 ряда с неотрицательными членами:
u1 +u2+u3+ … +un+ …(1)
v1 +v2+v3+ … +vn+ …(2)

Тогда
из сходимости ряда (2) => сходимость ряда (1),
и наоборот-
из расх. ряда (1) => расх. ряда (2).
Пример №1.
 , все ui ≥0
, все ui ≥0
1. 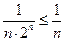
Но справа стоит общий член расходящегося гармонического ряда (см. пример свойства 4). Вопрос ОТКРЫТ.
2. 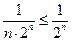
Справа общий член ряда геометрической прогрессии.

 .Следовательно, геом. прогрессия, а значит, и данный ряд сходится
.Следовательно, геом. прогрессия, а значит, и данный ряд сходится
Пример №2

 ряд расходится.
ряд расходится.
II Признак Д’Аламбера (1717-1784,фр)
Пусть для данного ряда u1 +u2+u3+ … +un+ … существует предел
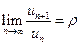 , тогда
, тогда 
Пример
№1
 =
= 
Ряд сходится
№2

 ;
;  ;
; 
 2>1 при n
2>1 при n 
 , ряд расходится
, ряд расходится
№3 Покажем, что в сомнительном случае  могут быть сходящиеся или расходящиеся ряды.
могут быть сходящиеся или расходящиеся ряды.
 - расх.
- расх.

 ,
,  , но ряд сходится, что видно из сравнения с рядом
, но ряд сходится, что видно из сравнения с рядом 


Сходимость ряда, общий член которого стоит справа, установлена раньше (пример 2, пункт 1).