Необходимый признак сходимости ряда
|
Теорема. Если ряд сходится, то  un=0.
Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел un=0.
Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел  =S. Тогда имеет место также равенство =S. Тогда имеет место также равенство  =S, так как при n =S, так как при n  и (n-1) и (n-1)  . Вычитая почленно из первого равенства второе, получаем . Вычитая почленно из первого равенства второе, получаем 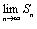 - -  = =  = =  un=0, что и требовалось доказать.
Следствие. Если un=0, что и требовалось доказать.
Следствие. Если  un≠0, то ряд u1+u2+…+un… расходится.
Пример.
Ряд un≠0, то ряд u1+u2+…+un… расходится.
Пример.
Ряд  расходится, так как расходится, так как
 un= un=  .
Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что .
Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что  un=0 не следует, что ряд сходится.
Позже докажем, что так называемый гармонический ряд un=0 не следует, что ряд сходится.
Позже докажем, что так называемый гармонический ряд
 (6)
расходится, хотя (6)
расходится, хотя  un= un=  Этот ряд часто будет использоваться в дальнейшем.
Этот ряд часто будет использоваться в дальнейшем.
|
| §4. Достаточные признаки сходимости знакоположительных числовых рядов
|
Определение 4. Числовой ряд называется знакоположительным, если un>0 при всех n=1,2,3… .
Нахождение суммы ряда S=  часто связано с большими техническими трудностями. В таких случаях сумму находят приближённо: S≈Sn. Последнее равенство тем точнее, чем больше n, при условии, что ряд сходится. Сходимость или расходимость ряда во многих случаях можно установить с помощью достаточных признаков сходимости числовых рядов. В этом параграфе будем рассматривать знакоположительные числовые ряды. Для таких рядов частичные суммы S1, S2, …,Sn,… образуют возрастающую числовую последовательность S1<S2<…<Sn<… .
Возможны два случая:
1) последовательность частичных сумм неограничена; в этом случае часто связано с большими техническими трудностями. В таких случаях сумму находят приближённо: S≈Sn. Последнее равенство тем точнее, чем больше n, при условии, что ряд сходится. Сходимость или расходимость ряда во многих случаях можно установить с помощью достаточных признаков сходимости числовых рядов. В этом параграфе будем рассматривать знакоположительные числовые ряды. Для таких рядов частичные суммы S1, S2, …,Sn,… образуют возрастающую числовую последовательность S1<S2<…<Sn<… .
Возможны два случая:
1) последовательность частичных сумм неограничена; в этом случае  =∞ и ряд расходится;
2) последовательность частичных сумм ограничена, то есть существует такое число С>0, что Sn<C при любых n=1,2,… . В этом случае существует конечный предел =∞ и ряд расходится;
2) последовательность частичных сумм ограничена, то есть существует такое число С>0, что Sn<C при любых n=1,2,… . В этом случае существует конечный предел  , следовательно, ряд сходится.
Таким образом, для доказательства сходимости знакоположительного числового ряда достаточно доказать ограниченность последовательности его частичных сумм.
Теорема 4. (Признак сравнения)
Пусть даны два знакоположительных числовых ряда , следовательно, ряд сходится.
Таким образом, для доказательства сходимости знакоположительного числового ряда достаточно доказать ограниченность последовательности его частичных сумм.
Теорема 4. (Признак сравнения)
Пусть даны два знакоположительных числовых ряда
 (7) (7)
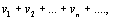 (8)
причём un≤vn при любых n=1,2,… .
Тогда: 1. Если ряд (8) сходится, то сходится и ряд (7);
2. Если ряд (7) расходится, то расходится и ряд (8).
Доказательство. Обозначим n-е частичные суммы рядов (7) и (8) через Sn и sn соответственно. Пусть ряд (8) сходится. Это значит, что существует конечный (8)
причём un≤vn при любых n=1,2,… .
Тогда: 1. Если ряд (8) сходится, то сходится и ряд (7);
2. Если ряд (7) расходится, то расходится и ряд (8).
Доказательство. Обозначим n-е частичные суммы рядов (7) и (8) через Sn и sn соответственно. Пусть ряд (8) сходится. Это значит, что существует конечный  =s. По условию теоремы 0< un≤vn, поэтому Sn<sn<s при всех n=1,2,… , то есть последовательность {Sn} ограничена, следовательно, ряд (7) сходится. Пусть теперь ряд (7) расходится, то есть =s. По условию теоремы 0< un≤vn, поэтому Sn<sn<s при всех n=1,2,… , то есть последовательность {Sn} ограничена, следовательно, ряд (7) сходится. Пусть теперь ряд (7) расходится, то есть  =∞. Тогда из неравенства Sn<sn следует, что и =∞. Тогда из неравенства Sn<sn следует, что и  =∞, следовательно, ряд (8) расходится. Теорема доказана.
Замечания.
1. В силу теоремы 1 признак сравнения справедлив и в случае, если un≤vn начиная с некоторого номера к, то есть при n≥k.
2. Для использования признака сравнения нужно иметь для сравнения ряды, про которые заранее известно, сходятся они или расходятся. В качестве таких рядов можно использовать сходящуюся бесконечно убывающую геометрическую прогрессию, а также обобщённые гармонические ряды =∞, следовательно, ряд (8) расходится. Теорема доказана.
Замечания.
1. В силу теоремы 1 признак сравнения справедлив и в случае, если un≤vn начиная с некоторого номера к, то есть при n≥k.
2. Для использования признака сравнения нужно иметь для сравнения ряды, про которые заранее известно, сходятся они или расходятся. В качестве таких рядов можно использовать сходящуюся бесконечно убывающую геометрическую прогрессию, а также обобщённые гармонические ряды  где к – действительное число. Несколько позже будет доказано, что при к≤1 такие ряды расходятся, а при k>1 сходятся. При к=1 получаем уже упоминавшийся расходящийся гармонический ряд.
Пример
Исследовать на сходимость ряд где к – действительное число. Несколько позже будет доказано, что при к≤1 такие ряды расходятся, а при k>1 сходятся. При к=1 получаем уже упоминавшийся расходящийся гармонический ряд.
Пример
Исследовать на сходимость ряд
 .
Рассмотрим расходящийся ряд .
Рассмотрим расходящийся ряд  Он расходится, так как получен из гармонического ряда отбрасыванием u1=1. Так как ln(n+1)<n+1 при любом n=1,2,…, то
Он расходится, так как получен из гармонического ряда отбрасыванием u1=1. Так как ln(n+1)<n+1 при любом n=1,2,…, то  поэтому данный ряд расходится по признаку сравнения.
Теорема 5. (Предельный признак сравнения)
Пусть даны два знакоположительных числовых ряда (7) и (8). Если существует конечный предел поэтому данный ряд расходится по признаку сравнения.
Теорема 5. (Предельный признак сравнения)
Пусть даны два знакоположительных числовых ряда (7) и (8). Если существует конечный предел  ≠0, то ряды (7) и (8) сходятся или расходятся одновременно.
Доказательство. По условию теоремы существует конечный предел ≠0, то ряды (7) и (8) сходятся или расходятся одновременно.
Доказательство. По условию теоремы существует конечный предел  . Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n≥Nвыполняется условие . Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n≥Nвыполняется условие  Последнее неравенство равносильно двойному неравенству –E< Последнее неравенство равносильно двойному неравенству –E<  -A<E или A-E< -A<E или A-E<  <A+E или <A+E или
 (9)
Неравенство (9) верно при любом E>0. Выберем поэтому Е так, чтобы выполнялось А-Е>0. Если ряд (8) сходится, то сходится и ряд (9)
Неравенство (9) верно при любом E>0. Выберем поэтому Е так, чтобы выполнялось А-Е>0. Если ряд (8) сходится, то сходится и ряд  по теореме 2. Но тогда по признаку сравнения, учитывая (9), сходится и ряд (7). Если ряд (7) сходится, то по признаку сравнения, учитывая (9), сходится ряд по теореме 2. Но тогда по признаку сравнения, учитывая (9), сходится и ряд (7). Если ряд (7) сходится, то по признаку сравнения, учитывая (9), сходится ряд  и по теореме 2 сходится ряд (8). Аналогично доказывается, учитывая (9), что из расходимости одного из рядов следует расходимость другого ряда. Докажите эту часть самостоятельно.
Замечание. Предельный признак сравнения рекомендуется применять в тех случаях, когда общий член ряда представляет собой отношение степенных функций. Для сравнения выбирается обобщённый гармонический ряд, общий член которого равен отношению старших степеней числителя и знаменателя общего члена данного ряда.
Пример.
Исследовать на сходимость ряд и по теореме 2 сходится ряд (8). Аналогично доказывается, учитывая (9), что из расходимости одного из рядов следует расходимость другого ряда. Докажите эту часть самостоятельно.
Замечание. Предельный признак сравнения рекомендуется применять в тех случаях, когда общий член ряда представляет собой отношение степенных функций. Для сравнения выбирается обобщённый гармонический ряд, общий член которого равен отношению старших степеней числителя и знаменателя общего члена данного ряда.
Пример.
Исследовать на сходимость ряд  Здесь un= Здесь un=  Возьмём для сравнения ряд с общим членом vn=
Возьмём для сравнения ряд с общим членом vn=  то есть расходящийся гармонический ряд то есть расходящийся гармонический ряд  Применим предельный признак сравнения. Применим предельный признак сравнения.
  ¹0,
следовательно, данный ряд расходится по предельному признаку сравнения.
Теорема 6. (Признак Даламбера)
Пусть дан знакоположительный числовой ряд ¹0,
следовательно, данный ряд расходится по предельному признаку сравнения.
Теорема 6. (Признак Даламбера)
Пусть дан знакоположительный числовой ряд
 (7)
и пусть существует предел (7)
и пусть существует предел  При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.
Доказательство. По условию существует предел При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.
Доказательство. По условию существует предел  . Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n³N выполняется условие . Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n³N выполняется условие  или
p-E< или
p-E<  (10)
Пусть сначала p<1. Выберем Е так, что p+E=q<1. Для всех n³N имеем (10)
Пусть сначала p<1. Выберем Е так, что p+E=q<1. Для всех n³N имеем    … или … или
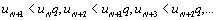 или
или
 (11)
Рассмотрим ряды (11)
Рассмотрим ряды
 (12) (12)
 . (13)
Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.
Пусть теперь p>1. Выберем Е так, что p-E>1. Тогда из левой части неравенства (10) следует, что при n³N выполняется . (13)
Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.
Пусть теперь p>1. Выберем Е так, что p-E>1. Тогда из левой части неравенства (10) следует, что при n³N выполняется  или un+1>un, то есть члены ряда возрастают с возрастанием номера n. Поэтому или un+1>un, то есть члены ряда возрастают с возрастанием номера n. Поэтому  un¹0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.
Замечания.
1. Если расходимость ряда установлена с помощью признака Даламбера, то un¹0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.
Замечания.
1. Если расходимость ряда установлена с помощью признака Даламбера, то  un¹0.
2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.
3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.
Пример.
Исследовать на сходимость ряд un¹0.
2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.
3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.
Пример.
Исследовать на сходимость ряд  Применим признак Даламбера. un=
Применим признак Даламбера. un=  un+1= un+1=  = =  . .   следовательно, ряд сходится по признаку Даламбера.
Теорема 7. (Признак Коши)
Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)
и пусть существует предел следовательно, ряд сходится по признаку Даламбера.
Теорема 7. (Признак Коши)
Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)
и пусть существует предел  При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.
Доказательство. По условию существует При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.
Доказательство. По условию существует  Это означает, что для любого положительного числа Е существует такой номер N, что для всех n³N выполняется условие | Это означает, что для любого положительного числа Е существует такой номер N, что для всех n³N выполняется условие | 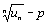 | <E или
p-E< | <E или
p-E<  <p+E. (14)
Пусть p<1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем <p+E. (14)
Пусть p<1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем  <q или un<qn для всех n³N. Рассмотрим ряды <q или un<qn для всех n³N. Рассмотрим ряды
 (15) (15)
 (16)
Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un<qn для всех n³N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).
Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие p-E >1. Тогда из (14) получаем (16)
Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un<qn для всех n³N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).
Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие p-E >1. Тогда из (14) получаем  >1 или un>1, следовательно, >1 или un>1, следовательно,  un¹0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.
Теорема 8. (Интегральный признак Коши)
Пусть члены знакоположительного числового ряда u1+u2+…+un… (7) не возрастают: u1³u2≥…≥un≥… и пусть f(x) такая положительная, непрерывная, невозрастающая на промежутке [1;∞) функция, чтоf(1)=u1, f(2)= u2 ,…, f(n)= =un,… . Тогда ряд (7) сходится или расходится одновременно с несобственным интегралом un¹0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.
Теорема 8. (Интегральный признак Коши)
Пусть члены знакоположительного числового ряда u1+u2+…+un… (7) не возрастают: u1³u2≥…≥un≥… и пусть f(x) такая положительная, непрерывная, невозрастающая на промежутке [1;∞) функция, чтоf(1)=u1, f(2)= u2 ,…, f(n)= =un,… . Тогда ряд (7) сходится или расходится одновременно с несобственным интегралом 
 Доказательство. Построим график функции y=f(x) на отрезке [1;n] и построим прямоугольник с основаниями [1;2], [2;3], …, [n-1;n] и высотами u1,u2,…,un-1, а также с высотами u2,u3,…,un.
Sn=u1+u2+…+un-1+un, Sвпис=u2.1+u3.1+…+un.1=u2+u3+…+un=Sn-u1,
Sопис=u1+u2+…+ +un-1=Sn-un.
Площадь криволинейной трапеции S=
Доказательство. Построим график функции y=f(x) на отрезке [1;n] и построим прямоугольник с основаниями [1;2], [2;3], …, [n-1;n] и высотами u1,u2,…,un-1, а также с высотами u2,u3,…,un.
Sn=u1+u2+…+un-1+un, Sвпис=u2.1+u3.1+…+un.1=u2+u3+…+un=Sn-u1,
Sопис=u1+u2+…+ +un-1=Sn-un.
Площадь криволинейной трапеции S=  . Получаем Sn-u1< . Получаем Sn-u1<  < Sn-un. Отсюда
Sn<u1+ < Sn-un. Отсюда
Sn<u1+  (17)
и Sn>un+ (17)
и Sn>un+  (18)
Пусть (18)
Пусть  сходится. Это означает, что существует конечный предел сходится. Это означает, что существует конечный предел   =Y. Соотношение (17) принимает вид: Sn<u1+Y при любом n. Это означает, что последовательность частичных суммSn ряда (7) ограничена и, следовательно, ряд (7) сходится. Пусть =Y. Соотношение (17) принимает вид: Sn<u1+Y при любом n. Это означает, что последовательность частичных суммSn ряда (7) ограничена и, следовательно, ряд (7) сходится. Пусть  расходится. Это означает, что расходится. Это означает, что   =∞ и тогда из (18) следует, что последовательность частичных сумм Sn ряда (7) неограничена и, следовательно, ряд (7) расходится. Теорема доказана.
Пример.
Исследуем с помощью интегрального признака Коши обобщённый гармонический ряд =∞ и тогда из (18) следует, что последовательность частичных сумм Sn ряда (7) неограничена и, следовательно, ряд (7) расходится. Теорема доказана.
Пример.
Исследуем с помощью интегрального признака Коши обобщённый гармонический ряд  Очевидно, f(x)=
Очевидно, f(x)= 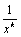 . При к≠1 имеем . При к≠1 имеем    = =  При к=1 имеем
При к=1 имеем   Таким образом, обобщённый гармонический ряд сходится при k>1 и расходится при k≤1.
Таким образом, обобщённый гармонический ряд сходится при k>1 и расходится при k≤1.
|
| Знакопеременные ряды
|
Определение 5. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.
Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на –1.
Изучение знакопеременных рядов начнём с частного случая – знакочередующихся рядов.
Определение 6. Числовой ряд вида u1-u2+u3-u4+…+ +(-1)n-1.un+…, где un – модуль члена ряда, называется знакочередующимся числовым рядом.
Теорема 9. (Признак Лейбница)
Если для знакочередующегося числового ряда
 (19)
Выполняются два условия:
Члены ряда убывают по модулю u1>u2>…>un>…, (19)
Выполняются два условия:
Члены ряда убывают по модулю u1>u2>…>un>…,
 то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда.
Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n).
По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n.
С другой стороны S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение в квадратных скобках положительно и S2n>0, поэтому S2n<u1 для любого n. Таким образом, последовательность частичных сумм S2n возрастает и ограничена, следовательно, существует конечный
то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда.
Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n).
По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n.
С другой стороны S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение в квадратных скобках положительно и S2n>0, поэтому S2n<u1 для любого n. Таким образом, последовательность частичных сумм S2n возрастает и ограничена, следовательно, существует конечный  S2n=S. При этом 0<S≤u1.
Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1=S2n+u2n+1. Перейдём в последнем равенстве к пределу при n→∞: S2n=S. При этом 0<S≤u1.
Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1=S2n+u2n+1. Перейдём в последнем равенстве к пределу при n→∞:  S2n+1= S2n+1=  S2n+ S2n+  u2n+1=S+0=S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют один и тот же предел S, поэтому u2n+1=S+0=S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют один и тот же предел S, поэтому  Sn=S, то есть данный ряд сходится. Теорема доказана.
Пример.
Исследовать на сходимость ряд Sn=S, то есть данный ряд сходится. Теорема доказана.
Пример.
Исследовать на сходимость ряд  Применим признак Лейбница.
un=
Применим признак Лейбница.
un=  >un+1= >un+1= 
 un= un=   Оба условия признака Лейбница выполняются, следовательно, ряд сходится.
Замечания.
1. Теорема Лейбница справедлива и если условие un>un+1 выполняется, начиная с некоторого номера N.
2. Условие un>un+1 не является необходимым. Ряд может сходиться, если оно не выполняется. Например, ряд
Оба условия признака Лейбница выполняются, следовательно, ряд сходится.
Замечания.
1. Теорема Лейбница справедлива и если условие un>un+1 выполняется, начиная с некоторого номера N.
2. Условие un>un+1 не является необходимым. Ряд может сходиться, если оно не выполняется. Например, ряд   сходится, как разность двух сходящихся рядов сходится, как разность двух сходящихся рядов  хотя условие un>un+1 не выполняется.
Определение 8. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно.
Определение 9. Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.
Пример.
Установить характер сходимости ряда хотя условие un>un+1 не выполняется.
Определение 8. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно.
Определение 9. Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.
Пример.
Установить характер сходимости ряда  Очевидно, что данный ряд сходится по признаку Лейбница. Действительно:
Очевидно, что данный ряд сходится по признаку Лейбница. Действительно:  и un= и un=  Ряд, составленный из абсолютных величин членов данного ряда
Ряд, составленный из абсолютных величин членов данного ряда  является расходящимся гармоническим рядом. Поэтому данный ряд сходится условно.
Теорема 10. (Достаточный признак сходимости знакопеременного ряда или признак абсолютной сходимости)
Пусть
u1+u2+…+un+…= является расходящимся гармоническим рядом. Поэтому данный ряд сходится условно.
Теорема 10. (Достаточный признак сходимости знакопеременного ряда или признак абсолютной сходимости)
Пусть
u1+u2+…+un+…=  (20)
знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов
│u1│+│ u2│+…+│ un │+…= (20)
знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов
│u1│+│ u2│+…+│ un │+…=  │ un │. (21)
Тогда ряд (20) тоже сходится.
Доказательство. Рассмотрим вспомогательный ряд
(u1+│u1│)+(u2+│u2│)+…+(un+│un│)+…= │ un │. (21)
Тогда ряд (20) тоже сходится.
Доказательство. Рассмотрим вспомогательный ряд
(u1+│u1│)+(u2+│u2│)+…+(un+│un│)+…=  (un+│un│). (22)
Очевидно, 0≤ un+│un│≤2│un│ при всех n=1, 2, … . Ряд (21) сходится по условию, поэтому сходится ряд (un+│un│). (22)
Очевидно, 0≤ un+│un│≤2│un│ при всех n=1, 2, … . Ряд (21) сходится по условию, поэтому сходится ряд  2│un│, тогда по признаку сравнения сходится ряд (22). Ряд (20) представляет собой разность двух сходящихся рядов (22) и (21), поэтому он тоже сходится. Теорема доказана.
Замечание.
Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться.
Например, ряд 2│un│, тогда по признаку сравнения сходится ряд (22). Ряд (20) представляет собой разность двух сходящихся рядов (22) и (21), поэтому он тоже сходится. Теорема доказана.
Замечание.
Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться.
Например, ряд   сходится по признаку Лейбница, а ряд сходится по признаку Лейбница, а ряд   расходится (это гармонический ряд).
Остаток ряда и его оценка
Рассмотрим сходящийся числовой ряд расходится (это гармонический ряд).
Остаток ряда и его оценка
Рассмотрим сходящийся числовой ряд
 (23)
Вычисление суммы ряда S= (23)
Вычисление суммы ряда S=  обычно технически очень сложно. Поэтому в качестве S берут S≈Sn. Точность этого равенства возрастает с увеличением n.
Определение 7. Если числовой ряд сходится, то разность Rn=S-Sn называется n-м остатком ряда.
Таким образом, Rn представляет собой сходящийся числовой ряд:
Rn= un+1+un+2+… .
Заметим, что обычно технически очень сложно. Поэтому в качестве S берут S≈Sn. Точность этого равенства возрастает с увеличением n.
Определение 7. Если числовой ряд сходится, то разность Rn=S-Sn называется n-м остатком ряда.
Таким образом, Rn представляет собой сходящийся числовой ряд:
Rn= un+1+un+2+… .
Заметим, что  Rn= Rn=  ( S-Sn)=S-S=0.
Абсолютная погрешность при замене суммы ряда S его частичной суммой Sn равна |Rn|=|S-Sn|. Таким образом, если требуется найти сумму ряда с точностью до E>0, то надо взять сумму такого числа nпервых членов ряда, чтобы выполнялось условие |Rn|<E. Однако в общем случае находить точно Rn не удаётся.
Теорема 11. (Об оценке остатка знакочередующегося числового ряда)
Если знакочередующийся числовой ряд сходится по признаку Лейбница, то его n-й остаток по абсолютной величине не превосходит модуля (n+1)-го члена ряда.
Доказательство. Пусть ряд u1-u2+u3-u4+…+(-1)n-1.un+… сходится по признаку Лейбница. Тогда n-й остаток ряда Rn=±(un+1-un+2+un+3-…) сам является суммой знакочередующегося числового ряда и по теореме Лейбница |Rn|≤|un+1|. Теорема доказана.
Пример.
Вычислить с точностью до 0,01 сумму ряда ( S-Sn)=S-S=0.
Абсолютная погрешность при замене суммы ряда S его частичной суммой Sn равна |Rn|=|S-Sn|. Таким образом, если требуется найти сумму ряда с точностью до E>0, то надо взять сумму такого числа nпервых членов ряда, чтобы выполнялось условие |Rn|<E. Однако в общем случае находить точно Rn не удаётся.
Теорема 11. (Об оценке остатка знакочередующегося числового ряда)
Если знакочередующийся числовой ряд сходится по признаку Лейбница, то его n-й остаток по абсолютной величине не превосходит модуля (n+1)-го члена ряда.
Доказательство. Пусть ряд u1-u2+u3-u4+…+(-1)n-1.un+… сходится по признаку Лейбница. Тогда n-й остаток ряда Rn=±(un+1-un+2+un+3-…) сам является суммой знакочередующегося числового ряда и по теореме Лейбница |Rn|≤|un+1|. Теорема доказана.
Пример.
Вычислить с точностью до 0,01 сумму ряда 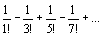 Очевидно, ряд сходится по признаку Лейбница. u1=
Очевидно, ряд сходится по признаку Лейбница. u1=  =1; u2= =1; u2=  ≈ ≈0,166; u3= ≈ ≈0,166; u3=  ≈0,008<0,01. Поэтому S≈1-0,166≈0,84. ≈0,008<0,01. Поэтому S≈1-0,166≈0,84.
|
| Степенные ряды
|
|
|
| §6. Основные понятия
|
Определение 10. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают: u1(x)+u2(x)+…+un(x)+… .
Определение 11. Если при x=x0 функциональный ряд сходится, то x0 называется точкой сходимости функционального ряда.
Определение 12. Множество всех точек сходимости функционального ряда называется его областью сходимости.
Очевидно, что в области сходимости функционального ряда его сумма является функцией от x. Будем обозначать её S(x).
Определение 13. Степенным рядом называется функциональный ряд вида
 , (24)
где a, a0, a1, a2, …, an, … – некоторые числа, называемые коэффициентами степенного ряда.
Теорема 12. (О структуре области сходимости степенного ряда)
Областью сходимости степенного ряда (24) является интервал (a-R;a+R), к которому в зависимости от конкретных случаев могут быть присоединены точки a-R и a+R, где R= , (24)
где a, a0, a1, a2, …, an, … – некоторые числа, называемые коэффициентами степенного ряда.
Теорема 12. (О структуре области сходимости степенного ряда)
Областью сходимости степенного ряда (24) является интервал (a-R;a+R), к которому в зависимости от конкретных случаев могут быть присоединены точки a-R и a+R, где R=  (если этот предел существует). В каждой точке интервала (a-R;a+R) ряд сходится абсолютно.
Доказательство. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
|a0|+|a1|.|x-a|+|a2|.|x-a|2+…+|an|.|x-a|n+… (25)
Применим к ряду (25) признак Даламбера (если этот предел существует). В каждой точке интервала (a-R;a+R) ряд сходится абсолютно.
Доказательство. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
|a0|+|a1|.|x-a|+|a2|.|x-a|2+…+|an|.|x-a|n+… (25)
Применим к ряду (25) признак Даламбера
  Возможны три случая:
1. Если
Возможны три случая:
1. Если  или |x-a|<R или xЄ(a-R;a+R), то ряд (25) сходится, но тогда по достаточному признаку сходимости знакопеременного ряда сходится и ряд (24), причём абсолютно.
2. Если или |x-a|<R или xЄ(a-R;a+R), то ряд (25) сходится, но тогда по достаточному признаку сходимости знакопеременного ряда сходится и ряд (24), причём абсолютно.
2. Если  , то ряд (25) расходится. В этом случае , то ряд (25) расходится. В этом случае  , то есть при достаточно больших n |un+1|>|un|, значит , то есть при достаточно больших n |un+1|>|un|, значит  ≠0 и ≠0 и  ≠0, следовательно, ряд (24) расходится по следствию из необходимого признака сходимости. Теорема доказана.
Определение 14. Интервал (a-R;a+R), называется интервалом сходимости степенного ряда, а половина его длины R называется радиусом сходимости степенного ряда.
Замечание. Любой степенной ряд (24) сходится при x=a. Если других точек сходимости у ряда (24) нет, то считают, что R=0. Если степенной ряд (24) сходится во всех точках числовой прямой, то считают, что R=∞.
Примеры.
Найти область сходимости степенного ряда.
1. ≠0, следовательно, ряд (24) расходится по следствию из необходимого признака сходимости. Теорема доказана.
Определение 14. Интервал (a-R;a+R), называется интервалом сходимости степенного ряда, а половина его длины R называется радиусом сходимости степенного ряда.
Замечание. Любой степенной ряд (24) сходится при x=a. Если других точек сходимости у ряда (24) нет, то считают, что R=0. Если степенной ряд (24) сходится во всех точках числовой прямой, то считают, что R=∞.
Примеры.
Найти область сходимости степенного ряда.
1.  Составим ряд из абсолютных величин членов данного ряда
Составим ряд из абсолютных величин членов данного ряда  и применим к нему признак Даламбера. |un|= и применим к нему признак Даламбера. |un|=  , |un+1|= , |un+1|=  , ,  = |x|. = |x|.  |x|. |x|.  |x|.
Ряд сходится, если |x|<1 или x |x|.
Ряд сходится, если |x|<1 или x  (-1;1) – это и есть интервал сходимости. Исследуем концы этого интервала. При x=1 получаем расходящийся обобщённый гармонический ряд (-1;1) – это и есть интервал сходимости. Исследуем концы этого интервала. При x=1 получаем расходящийся обобщённый гармонический ряд  . При x=-1 получаем знакочередующийся числовой ряд . При x=-1 получаем знакочередующийся числовой ряд  сходящийся по признаку Лейбница.
Действительно, сходящийся по признаку Лейбница.
Действительно,  = =  и |un|= и |un|=  |un+1|= |un+1|=  Таким образом, областью сходимости данного ряда является промежуток [-1;1); R=1.
2. Таким образом, областью сходимости данного ряда является промежуток [-1;1); R=1.
2. 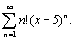 Составим ряд из абсолютных величин членов данного ряда
Составим ряд из абсолютных величин членов данного ряда  и применим к нему признак Даламбера. |un|=n!.|x-a|n, |un+1|=(n+1)!.|x-a|n+1, и применим к нему признак Даламбера. |un|=n!.|x-a|n, |un+1|=(n+1)!.|x-a|n+1,   = =  Таким образом, областью сходимости данного ряда является одна точка x=a; R=0.
3. Таким образом, областью сходимости данного ряда является одна точка x=a; R=0.
3.  Составим ряд из абсолютных величин членов данного ряда
Составим ряд из абсолютных величин членов данного ряда  и применим к нему признак Даламбера. |un|= и применим к нему признак Даламбера. |un|=  |un+1|= |un+1|=    при всех x. Таким образом, областью сходимости данного ряда является промежуток (-∞;+∞); R=∞.
Свойства степенных рядов
Отметим здесь без доказательства три важных свойства степенных рядов:
1. Сумма S(x) степенного ряда
S(x)=a0+a1(x-a)+a2(x-a)2+…+an(x-a)n+… (24)
является непрерывной функцией в каждой точке интервала сходимости (a-R;a+R).
2. Ряд
φ(x)=a1+2a2(x-a)+…+nan(x-a)n-1+…, (26)
полученный почленным дифференцированием ряда (24), является степенным рядом с тем же, что и ряд (24), интервалом сходимости (a-R;a+R). Сумма ряда (26) φ(x)=S'(x).
Замечание. Ряд (26) также можно почленно дифференцировать и сумма полученного после этого ряда равна при всех x. Таким образом, областью сходимости данного ряда является промежуток (-∞;+∞); R=∞.
Свойства степенных рядов
Отметим здесь без доказательства три важных свойства степенных рядов:
1. Сумма S(x) степенного ряда
S(x)=a0+a1(x-a)+a2(x-a)2+…+an(x-a)n+… (24)
является непрерывной функцией в каждой точке интервала сходимости (a-R;a+R).
2. Ряд
φ(x)=a1+2a2(x-a)+…+nan(x-a)n-1+…, (26)
полученный почленным дифференцированием ряда (24), является степенным рядом с тем же, что и ряд (24), интервалом сходимости (a-R;a+R). Сумма ряда (26) φ(x)=S'(x).
Замечание. Ряд (26) также можно почленно дифференцировать и сумма полученного после этого ряда равна  и так далее. Таким образом, сумма и так далее. Таким образом, сумма 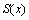 ряда (24) является бесконечно дифференцируемой функцией в интервале сходимости ряда (24) является бесконечно дифференцируемой функцией в интервале сходимости  . Сумма ряда, полученного из ряда (24) n-кратным дифференцированием равна . Сумма ряда, полученного из ряда (24) n-кратным дифференцированием равна  Область сходимости степенного ряда при дифференцируемости не меняется.
3. Пусть числа Область сходимости степенного ряда при дифференцируемости не меняется.
3. Пусть числа  и и  принадлежат интервалу сходимости принадлежат интервалу сходимости   ряда (24). Тогда имеет место равенство ряда (24). Тогда имеет место равенство

|
| Разложение функций в степенные ряды
|
Пусть функция f(x) бесконечно дифференцируема в (a-R;a+R) и является суммой степенного ряда
f(x)= a0+a1(x-a)+a2(x-a)2+…+an(x-a)n+…, (27)
где (a-R;a+R) – интервал сходимости ряда (27). В этом случае говорят, что функция f(x) разлагается в степенной ряд в окрестности точки а или по степеням (x-a). Определим коэффициенты a0, a1, a2, …,an,… ряда (27), для чего продифференцируем n раз ряд (27).
f(x)=a0+a1(x-a)+a2(x-a)2+ a3(x-a)3+ a4(x-a)4+…+an(x-a)n+…
f’(x)=a1+2a2(x-a)+3a3(x-a)2+ 4a4(x-a)3+…+nan(x-a)n-1+…
f′′(x)=2a2+3.2a3(x-a)+4.3a4(x-a)2+…+(n-1)nan(x-a)n-2+…
f′′′(x)=3.2a3+4.3.2a4(x-a)+…+(n-2)(n-1)nan(x-a)n-3+…
…………………………………………
f(n)(x)=2.3…(n-2)(n-1)nan+…
…………………………………………
Все ряды имеют интервал сходимости (a-R;a+R). При x=a из полученных тождеств получаем f(a)=a0, f’(a)=a1, f’’(a)=2a2, …, f(n)(a)= 2.3…(n-2)(n-1)nan, … . Отсюда находим коэффициенты степенного ряда (27): a0=f(a), a1=  a2= a2=  , a3= , a3=  , …, an= , …, an=  , … . Подставляя полученные значения коэффициентов в ряд (27), получаем
f(x)=f(a)+ , … . Подставляя полученные значения коэффициентов в ряд (27), получаем
f(x)=f(a)+  (x-a)+ (x-a)+  (x-a)2+…+ (x-a)2+…+  (x-a)n+… . (28)
ряд (28) называется рядом Тейлора для функции f(x) в точке a. В частном случае при a=0 ряд (28) принимает вид
f(x)=f(0)+ (x-a)n+… . (28)
ряд (28) называется рядом Тейлора для функции f(x) в точке a. В частном случае при a=0 ряд (28) принимает вид
f(x)=f(0)+   +…+ +…+  +… (29)
и называется рядом Маклорена.
Таким образом, если функция f(x) является суммой степенного ряда, то этот ряд называется рядом Тейлора для функции f(x).
Пусть теперь дана бесконечно дифференцируемая в точке a функция f(x). Составим для неё формально ряд Тейлора:
f(a)+ +… (29)
и называется рядом Маклорена.
Таким образом, если функция f(x) является суммой степенного ряда, то этот ряд называется рядом Тейлора для функции f(x).
Пусть теперь дана бесконечно дифференцируемая в точке a функция f(x). Составим для неё формально ряд Тейлора:
f(a)+  +…+ +…+  +… .
Совпадает ли сумма полученного ряда Тейлора с функцией f(x), для которой он составлен? Оказывается, не всегда. При каких условиях сумма ряда Тейлора совпадает с функцией, для которой он составлен? Рассмотрим n-ю частичную сумму ряда Тейлора
Sn(x)= f(a)+ +… .
Совпадает ли сумма полученного ряда Тейлора с функцией f(x), для которой он составлен? Оказывается, не всегда. При каких условиях сумма ряда Тейлора совпадает с функцией, для которой он составлен? Рассмотрим n-ю частичную сумму ряда Тейлора
Sn(x)= f(a)+  +…+ +…+  . (30)
Многочлен (30) называется многочленом Тейлора степени n. Разность Rn(x)=f(x)-Sn(x) называется остаточным членом ряда Тейлора. Приведём без доказательства следующую теорему.
Теорема 13.
Для того, чтобы бесконечно дифференцируемая в точке а функция f(x) являлась суммой составленного для неё ряда Тейлора, необходимо и достаточно, чтобы . (30)
Многочлен (30) называется многочленом Тейлора степени n. Разность Rn(x)=f(x)-Sn(x) называется остаточным членом ряда Тейлора. Приведём без доказательства следующую теорему.
Теорема 13.
Для того, чтобы бесконечно дифференцируемая в точке а функция f(x) являлась суммой составленного для неё ряда Тейлора, необходимо и достаточно, чтобы  Rn(x)=0.
Можно показать, что остаточный член можно представить в форме Лагранжа: Rn(x)= Rn(x)=0.
Можно показать, что остаточный член можно представить в форме Лагранжа: Rn(x)= 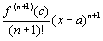 , где с – некоторое число из интервала (a;x). Таким образом
f(x)= f(a)+ , где с – некоторое число из интервала (a;x). Таким образом
f(x)= f(a)+  +…+ +…+  + +  31)
Формула (31) называется формулой Тейлора, а её частный случай при а=0 называется формулой Маклорена:
f(x)= f(0)+ 31)
Формула (31) называется формулой Тейлора, а её частный случай при а=0 называется формулой Маклорена:
f(x)= f(0)+  +…+ +…+  + + 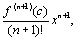 где с где с  (0;x). (0;x).
|
| Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
|
1. Разложение функции f(x)=ex в ряд Маклорена.
f(x)=f′(x)=f″(x)=…=f(n)(x)=…=ex.
f(0)=f′(0)=f″(0)=…=f(n)(0)=…=1.
Составим для функции f(x)=ex формально ряд Маклорена: 1+  .
Найдём области сходимости этого ряда. .
Найдём области сходимости этого ряда.
 при любых x, следовательно, областью сходимости ряда является промежуток (-∞;+∞). Заметим, что так как ряд сходится абсолютно, то при любых x, следовательно, областью сходимости ряда является промежуток (-∞;+∞). Заметим, что так как ряд сходится абсолютно, то  при любых хи тем более при любых хи тем более  при любых х. Так как f(n+1)(x)=ex и f(n+1)(с)=eс, то при любых х. Так как f(n+1)(x)=ex и f(n+1)(с)=eс, то   =ec =ec  =0. Таким образом, имеет место разложение при x =0. Таким образом, имеет место разложение при x  (-∞;+∞)
ex=1+ (-∞;+∞)
ex=1+  . (32)
2. Разложение функции f(x)=sinx в ряд Маклорена.
Вычислим производные данной функции.
f′(x)=cosx=sin(x+ . (32)
2. Разложение функции f(x)=sinx в ряд Маклорена.
Вычислим производные данной функции.
f′(x)=cosx=sin(x+  ), f″(x)=-sinx=sin(x+ ), f″(x)=-sinx=sin(x+  ),
f″′(x)=-cosx=sin(x+ ),
f″′(x)=-cosx=sin(x+  ), f(4)(x)=sinx=sin(x+ ), f(4)(x)=sinx=sin(x+  ), …, f(n)(x)=sin(x+ ), …, f(n)(x)=sin(x+  ), … . Вычислим значения f(x) и производных в точке 0: f(0)=0, f′(0)=1, f″(0)=0, f″′(0)=-1, f(4)(0)=0, …, f(2n-1)(0)=(-1)n-1,f(2n)(0)=0.
Исследуем остаточный член ряда.
|Rn(x)|= = ), … . Вычислим значения f(x) и производных в точке 0: f(0)=0, f′(0)=1, f″(0)=0, f″′(0)=-1, f(4)(0)=0, …, f(2n-1)(0)=(-1)n-1,f(2n)(0)=0.
Исследуем остаточный член ряда.
|Rn(x)|= =  так как |sin(c+(n+1) так как |sin(c+(n+1)  |≤1. Переходя к пределу при n→∞, получаем |≤1. Переходя к пределу при n→∞, получаем  следовательно, следовательно,  и и  . Рекомендуем показать самостоятельно, что областью сходимости ряда является промежуток (-∞;+∞). Таким образом, имеет место разложение при x . Рекомендуем показать самостоятельно, что областью сходимости ряда является промежуток (-∞;+∞). Таким образом, имеет место разложение при x  (-∞;+∞):
sinx=x- (-∞;+∞):
sinx=x-  . (33)
3. Разложение функции y=cosx в ряд Маклорена. Дифференцируя ряд (33), получаем разложение при x . (33)
3. Разложение функции y=cosx в ряд Маклорена. Дифференцируя ряд (33), получаем разложение при x  (-∞;+∞):
cosx=1- (-∞;+∞):
cosx=1-  . (34)
4. Биномиальный ряд.
Разложим в ряд Маклорена функцию f(x)=(1+x)m, где m≠0 – любое действительное число. Для этого вычислим производные: f′(x)=m(1+x)m-1, f″(x)=(m-1)m(1+x)m-2, f″′(x)=(m-2)(m-1)m(1+x)m-3, …, f(n)(x)=(m-n+1)…(m-2).(m-1)m(1+x)m-n, … При x=0 получаем f(0)=1, f′(0)=m, f″(0)=(m-1)m, f″′(0)=(m--2)(m-1)m, …, f(n)(0)=(m-n+1)…(m-2)(m-1)m, … .
Можно показать, что областью сходимости ряда является промежуток (-1;1) (на концах интервала ряд сходится или расходится в зависимости от конкретных значений m) и что . (34)
4. Биномиальный ряд.
Разложим в ряд Маклорена функцию f(x)=(1+x)m, где m≠0 – любое действительное число. Для этого вычислим производные: f′(x)=m(1+x)m-1, f″(x)=(m-1)m(1+x)m-2, f″′(x)=(m-2)(m-1)m(1+x)m-3, …, f(n)(x)=(m-n+1)…(m-2).(m-1)m(1+x)m-n, … При x=0 получаем f(0)=1, f′(0)=m, f″(0)=(m-1)m, f″′(0)=(m--2)(m-1)m, …, f(n)(0)=(m-n+1)…(m-2)(m-1)m, … .
Можно показать, что областью сходимости ряда является промежуток (-1;1) (на концах интервала ряд сходится или расходится в зависимости от конкретных значений m) и что  . Таким образом, при x . Таким образом, при x  (-1;1) имеет место разложение:
(1+x)m=1+ (-1;1) имеет место разложение:
(1+x)m=1+  + +  + +  +
+…+ +
+…+  . (35)
Ряд (35) называется биномиальным рядом.
5. Разложение функции f(x)=lnx в ряд Тейлора. При x=0 функция f(x)=lnx не определена, поэтому её нельзя разложить в ряд Маклорена. Разложим её в ряд Тейлора, например, по степеням (x-1). Для этого, вычислим производные: f′(x)=x-1, f″(x)=-1.x-2=-1!x-2, f″′(x)=1.2.x-3=2!x-3, f(4)(x)=-1.2. .3.x-4=-3!x-4, …, f(n)(x)=(-1)n-1. .(n-1)!x-n, … .
При x=1 получаем: f(1)=0, f′(1)=1, f″(1)=-1!, f″′(1)=2!, f(4)(1)=-3!, …, f(n)(1)=(-1)n-1(n-1)!, … .
Можно показать, что областью сходимости ряда является промежуток (0;2] и что . (35)
Ряд (35) называется биномиальным рядом.
5. Разложение функции f(x)=lnx в ряд Тейлора. При x=0 функция f(x)=lnx не определена, поэтому её нельзя разложить в ряд Маклорена. Разложим её в ряд Тейлора, например, по степеням (x-1). Для этого, вычислим производные: f′(x)=x-1, f″(x)=-1.x-2=-1!x-2, f″′(x)=1.2.x-3=2!x-3, f(4)(x)=-1.2. .3.x-4=-3!x-4, …, f(n)(x)=(-1)n-1. .(n-1)!x-n, … .
При x=1 получаем: f(1)=0, f′(1)=1, f″(1)=-1!, f″′(1)=2!, f(4)(1)=-3!, …, f(n)(1)=(-1)n-1(n-1)!, … .
Можно показать, что областью сходимости ряда является промежуток (0;2] и что  . Таким образом, при x . Таким образом, при x  (0;2] имеет место разложение:
lnx= (0;2] имеет место разложение:
lnx=  . (36)
Заметим, что разложение функций в ряды Тейлора или Маклорена непосредственно часто связано с громоздкими вычислениями при нахождении производных и исследовании остаточного члена. На примерах покажем некоторые приёмы, позволяющие избежать этих трудностей.
Примеры.
1. Разложить в степенной ряд функцию . (36)
Заметим, что разложение функций в ряды Тейлора или Маклорена непосредственно часто связано с громоздкими вычислениями при нахождении производных и исследовании остаточного члена. На примерах покажем некоторые приёмы, позволяющие избежать этих трудностей.
Примеры.
1. Разложить в степенной ряд функцию  .
В формуле (32) сделаем замену переменной x=-t2, получим .
В формуле (32) сделаем замену переменной x=-t2, получим
 при t при t  (-∞;+∞). Переобозначая t на x, получим нужное разложение: (-∞;+∞). Переобозначая t на x, получим нужное разложение:
 при x при x  (-∞;+∞).
2. Разложить в степенной ряд функцию f(x)= (-∞;+∞).
2. Разложить в степенной ряд функцию f(x)=  .
Очевидно, f(x)= .
Очевидно, f(x)=  . Обозначим x2=t и воспользуемся биноминальным рядом при m=-1. . Обозначим x2=t и воспользуемся биноминальным рядом при m=-1.
 = = 
 =1-t+t2-t3+…+(-1)n.tn+… , t =1-t+t2-t3+…+(-1)n.tn+… , t  (-1;1). (37)
Возвращаясь к переменной x, получаем разложение при x (-1;1). (37)
Возвращаясь к переменной x, получаем разложение при x  (-1;1): (-1;1):
 =1-x2+x4-x6+…+(-1)n.x2n+… . (38)
3. Разложить в ряд Маклорена функцию f(x)=ln(1+x).
Проинтегрируем обе части равенства (37) от 0 до x при x =1-x2+x4-x6+…+(-1)n.x2n+… . (38)
3. Разложить в ряд Маклорена функцию f(x)=ln(1+x).
Проинтегрируем обе части равенства (37) от 0 до x при x  (-1;1). Получим (-1;1). Получим
 или
ln(1+x)=x
или
ln(1+x)=x  . (39)
Можно показать, что ряд (39) имеет область сходимости (-1;1].
4. Разложить в степенной ряд функцию f(x)=arctgx.
Проинтегрируем обе части равенства (38) от 0 до x при x . (39)
Можно показать, что ряд (39) имеет область сходимости (-1;1].
4. Разложить в степенной ряд функцию f(x)=arctgx.
Проинтегрируем обе части равенства (38) от 0 до x при x  (-1;1): (-1;1):
 или
arctgx=x
или
arctgx=x 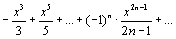 . (40)
Можно показать, что ряд (40) имеет область сходимости [-1;1]. . (40)
Можно показать, что ряд (40) имеет область сходимости [-1;1].
|
| Применение рядов к приближённым вычислениям
|
Числовые и функциональные ряды широко применяются в приближённых вычислениях. Рассмотрим это на примерах.
Пример 1.
Вычислить  с точностью до 0,001.
Воспользуемся разложением с точностью до 0,001.
Воспользуемся разложением  Тогда Тогда
 = =     0,0238+0,0046– –0,0008≈0,7475≈0,748.
Так как ряд знакочередующийся и 0,0008<0,001, то все слагаемые, начиная с 0,0008, отбрасываем и при этом погрешность не превосходит 0,001.
Пример 2.
Вычислить 0,0238+0,0046– –0,0008≈0,7475≈0,748.
Так как ряд знакочередующийся и 0,0008<0,001, то все слагаемые, начиная с 0,0008, отбрасываем и при этом погрешность не превосходит 0,001.
Пример 2.
Вычислить  с точностью до 0,001. с точностью до 0,001.
 = =  Используем биномиальный ряд при x=0.25; m= Используем биномиальный ряд при x=0.25; m= 
 ≈2(1+ ≈2(1+  +
+  2.(1+0,0833--0,0069+0,00096) ≈ ≈2.(1+0,0833-0,0069) ≈2,1528≈2,153.
Так как, начиная со второго члена, ряд знакочередующийся и 0,00096<0,001, то все слагаемые, начиная с 0,00096, отбрасываем и при этом погрешность не превосходит 0,001.
Пример 3.
Вычислить e0,1 с точностью до 0,001.
Для функции ex формула Тейлора имеет вид: ex=1+x+ 2.(1+0,0833--0,0069+0,00096) ≈ ≈2.(1+0,0833-0,0069) ≈2,1528≈2,153.
Так как, начиная со второго члена, ряд знакочередующийся и 0,00096<0,001, то все слагаемые, начиная с 0,00096, отбрасываем и при этом погрешность не превосходит 0,001.
Пример 3.
Вычислить e0,1 с точностью до 0,001.
Для функции ex формула Тейлора имеет вид: ex=1+x+ 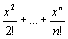 +Rn(x), где Rn(x)= +Rn(x), где Rn(x)=  где с где с  (0;x).
При x=0.1 получаем знакоположительный числовой ряд. Так как при этом с (0;x).
При x=0.1 получаем знакоположительный числовой ряд. Так как при этом с  (0;0,1), 0,1 (0;0,1), 0,1  [0;0,5], то 0<c<0,1<0,5 и ec<e0,5<2. Тогда [0;0,5], то 0<c<0,1<0,5 и ec<e0,5<2. Тогда  Необходимо взять столько членов ряда, чтобы выполнялось условие: Необходимо взять столько членов ряда, чтобы выполнялось условие:  0,001 или 0,001 или  0,0005.
При x=0,1 получаем
e0,1≈1+0,1+ 0,0005.
При x=0,1 получаем
e0,1≈1+0,1+  ≈1+0,1+0,005+0,0002≈1,1052≈1,105.
Так как 0,0002<0,0005, то достаточно взять четыре члена ряда.
Пример 4.
Проинтегрировать дифференциальное уравнение y′=y+x2, y(0)=-2 методом последовательного дифференцирования.
Будем искать решение в виде ряда Маклорена:
y(x)=y(0)+ ≈1+0,1+0,005+0,0002≈1,1052≈1,105.
Так как 0,0002<0,0005, то достаточно взять четыре члена ряда.
Пример 4.
Проинтегрировать дифференциальное уравнение y′=y+x2, y(0)=-2 методом последовательного дифференцирования.
Будем искать решение в виде ряда Маклорена:
y(x)=y(0)+  .
Вычислим производные: y′=y+x2, y″=y′+2x, y″′=y″+2, y(4)= y″′, …, y(n)= y″′ при n=4, 5, … .
При x=0 получаем: y(0)=-2, y′(0)=-2, y″(0)=-2, y(n)(0)=0 при n=3, 4, 5. Окончательно получаем y(x)=-2-2x-x2. .
Вычислим производные: y′=y+x2, y″=y′+2x, y″′=y″+2, y(4)= y″′, …, y(n)= y″′ при n=4, 5, … .
При x=0 получаем: y(0)=-2, y′(0)=-2, y″(0)=-2, y(n)(0)=0 при n=3, 4, 5. Окончательно получаем y(x)=-2-2x-x2.
|
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.
 un=0.
Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел
un=0.
Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел  =S. Тогда имеет место также равенство
=S. Тогда имеет место также равенство  =S, так как при n
=S, так как при n  и (n-1)
и (n-1)  . Вычитая почленно из первого равенства второе, получаем
. Вычитая почленно из первого равенства второе, получаем 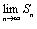 -
-  =
=  =
=  un=0, что и требовалось доказать.
Следствие. Если
un=0, что и требовалось доказать.
Следствие. Если  un≠0, то ряд u1+u2+…+un… расходится.
Пример.
Ряд
un≠0, то ряд u1+u2+…+un… расходится.
Пример.
Ряд  расходится, так как
расходится, так как
 un=
un=  .
Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что
.
Подчеркнём, что рассмотренный признак является только необходимым, но не достаточным, то есть из того, что  un=0 не следует, что ряд сходится.
Позже докажем, что так называемый гармонический ряд
un=0 не следует, что ряд сходится.
Позже докажем, что так называемый гармонический ряд
 (6)
расходится, хотя
(6)
расходится, хотя  un=
un=  Этот ряд часто будет использоваться в дальнейшем.
Этот ряд часто будет использоваться в дальнейшем.
 часто связано с большими техническими трудностями. В таких случаях сумму находят приближённо: S≈Sn. Последнее равенство тем точнее, чем больше n, при условии, что ряд сходится. Сходимость или расходимость ряда во многих случаях можно установить с помощью достаточных признаков сходимости числовых рядов. В этом параграфе будем рассматривать знакоположительные числовые ряды. Для таких рядов частичные суммы S1, S2, …,Sn,… образуют возрастающую числовую последовательность S1<S2<…<Sn<… .
Возможны два случая:
1) последовательность частичных сумм неограничена; в этом случае
часто связано с большими техническими трудностями. В таких случаях сумму находят приближённо: S≈Sn. Последнее равенство тем точнее, чем больше n, при условии, что ряд сходится. Сходимость или расходимость ряда во многих случаях можно установить с помощью достаточных признаков сходимости числовых рядов. В этом параграфе будем рассматривать знакоположительные числовые ряды. Для таких рядов частичные суммы S1, S2, …,Sn,… образуют возрастающую числовую последовательность S1<S2<…<Sn<… .
Возможны два случая:
1) последовательность частичных сумм неограничена; в этом случае  =∞ и ряд расходится;
2) последовательность частичных сумм ограничена, то есть существует такое число С>0, что Sn<C при любых n=1,2,… . В этом случае существует конечный предел
=∞ и ряд расходится;
2) последовательность частичных сумм ограничена, то есть существует такое число С>0, что Sn<C при любых n=1,2,… . В этом случае существует конечный предел  , следовательно, ряд сходится.
Таким образом, для доказательства сходимости знакоположительного числового ряда достаточно доказать ограниченность последовательности его частичных сумм.
Теорема 4. (Признак сравнения)
Пусть даны два знакоположительных числовых ряда
, следовательно, ряд сходится.
Таким образом, для доказательства сходимости знакоположительного числового ряда достаточно доказать ограниченность последовательности его частичных сумм.
Теорема 4. (Признак сравнения)
Пусть даны два знакоположительных числовых ряда
 (7)
(7)
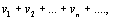 (8)
причём un≤vn при любых n=1,2,… .
Тогда: 1. Если ряд (8) сходится, то сходится и ряд (7);
2. Если ряд (7) расходится, то расходится и ряд (8).
Доказательство. Обозначим n-е частичные суммы рядов (7) и (8) через Sn и sn соответственно. Пусть ряд (8) сходится. Это значит, что существует конечный
(8)
причём un≤vn при любых n=1,2,… .
Тогда: 1. Если ряд (8) сходится, то сходится и ряд (7);
2. Если ряд (7) расходится, то расходится и ряд (8).
Доказательство. Обозначим n-е частичные суммы рядов (7) и (8) через Sn и sn соответственно. Пусть ряд (8) сходится. Это значит, что существует конечный  =s. По условию теоремы 0< un≤vn, поэтому Sn<sn<s при всех n=1,2,… , то есть последовательность {Sn} ограничена, следовательно, ряд (7) сходится. Пусть теперь ряд (7) расходится, то есть
=s. По условию теоремы 0< un≤vn, поэтому Sn<sn<s при всех n=1,2,… , то есть последовательность {Sn} ограничена, следовательно, ряд (7) сходится. Пусть теперь ряд (7) расходится, то есть  =∞. Тогда из неравенства Sn<sn следует, что и
=∞. Тогда из неравенства Sn<sn следует, что и  =∞, следовательно, ряд (8) расходится. Теорема доказана.
Замечания.
1. В силу теоремы 1 признак сравнения справедлив и в случае, если un≤vn начиная с некоторого номера к, то есть при n≥k.
2. Для использования признака сравнения нужно иметь для сравнения ряды, про которые заранее известно, сходятся они или расходятся. В качестве таких рядов можно использовать сходящуюся бесконечно убывающую геометрическую прогрессию, а также обобщённые гармонические ряды
=∞, следовательно, ряд (8) расходится. Теорема доказана.
Замечания.
1. В силу теоремы 1 признак сравнения справедлив и в случае, если un≤vn начиная с некоторого номера к, то есть при n≥k.
2. Для использования признака сравнения нужно иметь для сравнения ряды, про которые заранее известно, сходятся они или расходятся. В качестве таких рядов можно использовать сходящуюся бесконечно убывающую геометрическую прогрессию, а также обобщённые гармонические ряды  где к – действительное число. Несколько позже будет доказано, что при к≤1 такие ряды расходятся, а при k>1 сходятся. При к=1 получаем уже упоминавшийся расходящийся гармонический ряд.
Пример
Исследовать на сходимость ряд
где к – действительное число. Несколько позже будет доказано, что при к≤1 такие ряды расходятся, а при k>1 сходятся. При к=1 получаем уже упоминавшийся расходящийся гармонический ряд.
Пример
Исследовать на сходимость ряд
 .
Рассмотрим расходящийся ряд
.
Рассмотрим расходящийся ряд  Он расходится, так как получен из гармонического ряда отбрасыванием u1=1. Так как ln(n+1)<n+1 при любом n=1,2,…, то
Он расходится, так как получен из гармонического ряда отбрасыванием u1=1. Так как ln(n+1)<n+1 при любом n=1,2,…, то  поэтому данный ряд расходится по признаку сравнения.
Теорема 5. (Предельный признак сравнения)
Пусть даны два знакоположительных числовых ряда (7) и (8). Если существует конечный предел
поэтому данный ряд расходится по признаку сравнения.
Теорема 5. (Предельный признак сравнения)
Пусть даны два знакоположительных числовых ряда (7) и (8). Если существует конечный предел  ≠0, то ряды (7) и (8) сходятся или расходятся одновременно.
Доказательство. По условию теоремы существует конечный предел
≠0, то ряды (7) и (8) сходятся или расходятся одновременно.
Доказательство. По условию теоремы существует конечный предел  . Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n≥Nвыполняется условие
. Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n≥Nвыполняется условие  Последнее неравенство равносильно двойному неравенству –E<
Последнее неравенство равносильно двойному неравенству –E<  -A<E или A-E<
-A<E или A-E<  <A+E или
<A+E или
 (9)
Неравенство (9) верно при любом E>0. Выберем поэтому Е так, чтобы выполнялось А-Е>0. Если ряд (8) сходится, то сходится и ряд
(9)
Неравенство (9) верно при любом E>0. Выберем поэтому Е так, чтобы выполнялось А-Е>0. Если ряд (8) сходится, то сходится и ряд  по теореме 2. Но тогда по признаку сравнения, учитывая (9), сходится и ряд (7). Если ряд (7) сходится, то по признаку сравнения, учитывая (9), сходится ряд
по теореме 2. Но тогда по признаку сравнения, учитывая (9), сходится и ряд (7). Если ряд (7) сходится, то по признаку сравнения, учитывая (9), сходится ряд  и по теореме 2 сходится ряд (8). Аналогично доказывается, учитывая (9), что из расходимости одного из рядов следует расходимость другого ряда. Докажите эту часть самостоятельно.
Замечание. Предельный признак сравнения рекомендуется применять в тех случаях, когда общий член ряда представляет собой отношение степенных функций. Для сравнения выбирается обобщённый гармонический ряд, общий член которого равен отношению старших степеней числителя и знаменателя общего члена данного ряда.
Пример.
Исследовать на сходимость ряд
и по теореме 2 сходится ряд (8). Аналогично доказывается, учитывая (9), что из расходимости одного из рядов следует расходимость другого ряда. Докажите эту часть самостоятельно.
Замечание. Предельный признак сравнения рекомендуется применять в тех случаях, когда общий член ряда представляет собой отношение степенных функций. Для сравнения выбирается обобщённый гармонический ряд, общий член которого равен отношению старших степеней числителя и знаменателя общего члена данного ряда.
Пример.
Исследовать на сходимость ряд  Здесь un=
Здесь un=  Возьмём для сравнения ряд с общим членом vn=
Возьмём для сравнения ряд с общим членом vn=  то есть расходящийся гармонический ряд
то есть расходящийся гармонический ряд  Применим предельный признак сравнения.
Применим предельный признак сравнения.

 ¹0,
следовательно, данный ряд расходится по предельному признаку сравнения.
Теорема 6. (Признак Даламбера)
Пусть дан знакоположительный числовой ряд
¹0,
следовательно, данный ряд расходится по предельному признаку сравнения.
Теорема 6. (Признак Даламбера)
Пусть дан знакоположительный числовой ряд
 (7)
и пусть существует предел
(7)
и пусть существует предел  При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.
Доказательство. По условию существует предел
При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.
Доказательство. По условию существует предел  . Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n³N выполняется условие
. Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n³N выполняется условие  или
p-E<
или
p-E<  (10)
Пусть сначала p<1. Выберем Е так, что p+E=q<1. Для всех n³N имеем
(10)
Пусть сначала p<1. Выберем Е так, что p+E=q<1. Для всех n³N имеем 

 … или
… или
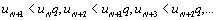 или
или
 (11)
Рассмотрим ряды
(11)
Рассмотрим ряды
 (12)
(12)
 . (13)
Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.
Пусть теперь p>1. Выберем Е так, что p-E>1. Тогда из левой части неравенства (10) следует, что при n³N выполняется
. (13)
Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.
Пусть теперь p>1. Выберем Е так, что p-E>1. Тогда из левой части неравенства (10) следует, что при n³N выполняется  или un+1>un, то есть члены ряда возрастают с возрастанием номера n. Поэтому
или un+1>un, то есть члены ряда возрастают с возрастанием номера n. Поэтому  un¹0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.
Замечания.
1. Если расходимость ряда установлена с помощью признака Даламбера, то
un¹0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.
Замечания.
1. Если расходимость ряда установлена с помощью признака Даламбера, то  un¹0.
2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.
3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.
Пример.
Исследовать на сходимость ряд
un¹0.
2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.
3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.
Пример.
Исследовать на сходимость ряд  Применим признак Даламбера. un=
Применим признак Даламбера. un=  un+1=
un+1=  =
=  .
. 
 следовательно, ряд сходится по признаку Даламбера.
Теорема 7. (Признак Коши)
Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)
и пусть существует предел
следовательно, ряд сходится по признаку Даламбера.
Теорема 7. (Признак Коши)
Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)
и пусть существует предел  При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.
Доказательство. По условию существует
При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.
Доказательство. По условию существует  Это означает, что для любого положительного числа Е существует такой номер N, что для всех n³N выполняется условие |
Это означает, что для любого положительного числа Е существует такой номер N, что для всех n³N выполняется условие | 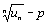 | <E или
p-E<
| <E или
p-E<  <p+E. (14)
Пусть p<1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем
<p+E. (14)
Пусть p<1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем  <q или un<qn для всех n³N. Рассмотрим ряды
<q или un<qn для всех n³N. Рассмотрим ряды
 (15)
(15)
 (16)
Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un<qn для всех n³N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).
Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие p-E >1. Тогда из (14) получаем
(16)
Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un<qn для всех n³N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).
Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие p-E >1. Тогда из (14) получаем  >1 или un>1, следовательно,
>1 или un>1, следовательно,  un¹0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.
Теорема 8. (Интегральный признак Коши)
Пусть члены знакоположительного числового ряда u1+u2+…+un… (7) не возрастают: u1³u2≥…≥un≥… и пусть f(x) такая положительная, непрерывная, невозрастающая на промежутке [1;∞) функция, чтоf(1)=u1, f(2)= u2 ,…, f(n)= =un,… . Тогда ряд (7) сходится или расходится одновременно с несобственным интегралом
un¹0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.
Теорема 8. (Интегральный признак Коши)
Пусть члены знакоположительного числового ряда u1+u2+…+un… (7) не возрастают: u1³u2≥…≥un≥… и пусть f(x) такая положительная, непрерывная, невозрастающая на промежутке [1;∞) функция, чтоf(1)=u1, f(2)= u2 ,…, f(n)= =un,… . Тогда ряд (7) сходится или расходится одновременно с несобственным интегралом 
 Доказательство. Построим график функции y=f(x) на отрезке [1;n] и построим прямоугольник с основаниями [1;2], [2;3], …, [n-1;n] и высотами u1,u2,…,un-1, а также с высотами u2,u3,…,un.
Sn=u1+u2+…+un-1+un, Sвпис=u2.1+u3.1+…+un.1=u2+u3+…+un=Sn-u1,
Sопис=u1+u2+…+ +un-1=Sn-un.
Площадь криволинейной трапеции S=
Доказательство. Построим график функции y=f(x) на отрезке [1;n] и построим прямоугольник с основаниями [1;2], [2;3], …, [n-1;n] и высотами u1,u2,…,un-1, а также с высотами u2,u3,…,un.
Sn=u1+u2+…+un-1+un, Sвпис=u2.1+u3.1+…+un.1=u2+u3+…+un=Sn-u1,
Sопис=u1+u2+…+ +un-1=Sn-un.
Площадь криволинейной трапеции S=  . Получаем Sn-u1<
. Получаем Sn-u1<  < Sn-un. Отсюда
Sn<u1+
< Sn-un. Отсюда
Sn<u1+  (17)
и Sn>un+
(17)
и Sn>un+  (18)
Пусть
(18)
Пусть  сходится. Это означает, что существует конечный предел
сходится. Это означает, что существует конечный предел 
 =Y. Соотношение (17) принимает вид: Sn<u1+Y при любом n. Это означает, что последовательность частичных суммSn ряда (7) ограничена и, следовательно, ряд (7) сходится. Пусть
=Y. Соотношение (17) принимает вид: Sn<u1+Y при любом n. Это означает, что последовательность частичных суммSn ряда (7) ограничена и, следовательно, ряд (7) сходится. Пусть  расходится. Это означает, что
расходится. Это означает, что 
 =∞ и тогда из (18) следует, что последовательность частичных сумм Sn ряда (7) неограничена и, следовательно, ряд (7) расходится. Теорема доказана.
Пример.
Исследуем с помощью интегрального признака Коши обобщённый гармонический ряд
=∞ и тогда из (18) следует, что последовательность частичных сумм Sn ряда (7) неограничена и, следовательно, ряд (7) расходится. Теорема доказана.
Пример.
Исследуем с помощью интегрального признака Коши обобщённый гармонический ряд  Очевидно, f(x)=
Очевидно, f(x)= 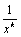 . При к≠1 имеем
. При к≠1 имеем 

 =
=  При к=1 имеем
При к=1 имеем 
 Таким образом, обобщённый гармонический ряд сходится при k>1 и расходится при k≤1.
Таким образом, обобщённый гармонический ряд сходится при k>1 и расходится при k≤1.
 (19)
Выполняются два условия:
Члены ряда убывают по модулю u1>u2>…>un>…,
(19)
Выполняются два условия:
Члены ряда убывают по модулю u1>u2>…>un>…,
 то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда.
Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n).
По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n.
С другой стороны S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение в квадратных скобках положительно и S2n>0, поэтому S2n<u1 для любого n. Таким образом, последовательность частичных сумм S2n возрастает и ограничена, следовательно, существует конечный
то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда.
Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n).
По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n.
С другой стороны S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение в квадратных скобках положительно и S2n>0, поэтому S2n<u1 для любого n. Таким образом, последовательность частичных сумм S2n возрастает и ограничена, следовательно, существует конечный  S2n=S. При этом 0<S≤u1.
Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1=S2n+u2n+1. Перейдём в последнем равенстве к пределу при n→∞:
S2n=S. При этом 0<S≤u1.
Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1=S2n+u2n+1. Перейдём в последнем равенстве к пределу при n→∞:  S2n+1=
S2n+1=  S2n+
S2n+  u2n+1=S+0=S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют один и тот же предел S, поэтому
u2n+1=S+0=S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют один и тот же предел S, поэтому  Sn=S, то есть данный ряд сходится. Теорема доказана.
Пример.
Исследовать на сходимость ряд
Sn=S, то есть данный ряд сходится. Теорема доказана.
Пример.
Исследовать на сходимость ряд  Применим признак Лейбница.
un=
Применим признак Лейбница.
un=  >un+1=
>un+1= 
 un=
un= 
 Оба условия признака Лейбница выполняются, следовательно, ряд сходится.
Замечания.
1. Теорема Лейбница справедлива и если условие un>un+1 выполняется, начиная с некоторого номера N.
2. Условие un>un+1 не является необходимым. Ряд может сходиться, если оно не выполняется. Например, ряд
Оба условия признака Лейбница выполняются, следовательно, ряд сходится.
Замечания.
1. Теорема Лейбница справедлива и если условие un>un+1 выполняется, начиная с некоторого номера N.
2. Условие un>un+1 не является необходимым. Ряд может сходиться, если оно не выполняется. Например, ряд 
 сходится, как разность двух сходящихся рядов
сходится, как разность двух сходящихся рядов  хотя условие un>un+1 не выполняется.
Определение 8. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно.
Определение 9. Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.
Пример.
Установить характер сходимости ряда
хотя условие un>un+1 не выполняется.
Определение 8. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно.
Определение 9. Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.
Пример.
Установить характер сходимости ряда  Очевидно, что данный ряд сходится по признаку Лейбница. Действительно:
Очевидно, что данный ряд сходится по признаку Лейбница. Действительно:  и un=
и un=  Ряд, составленный из абсолютных величин членов данного ряда
Ряд, составленный из абсолютных величин членов данного ряда  является расходящимся гармоническим рядом. Поэтому данный ряд сходится условно.
Теорема 10. (Достаточный признак сходимости знакопеременного ряда или признак абсолютной сходимости)
Пусть
u1+u2+…+un+…=
является расходящимся гармоническим рядом. Поэтому данный ряд сходится условно.
Теорема 10. (Достаточный признак сходимости знакопеременного ряда или признак абсолютной сходимости)
Пусть
u1+u2+…+un+…=  (20)
знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов
│u1│+│ u2│+…+│ un │+…=
(20)
знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов
│u1│+│ u2│+…+│ un │+…=  │ un │. (21)
Тогда ряд (20) тоже сходится.
Доказательство. Рассмотрим вспомогательный ряд
(u1+│u1│)+(u2+│u2│)+…+(un+│un│)+…=
│ un │. (21)
Тогда ряд (20) тоже сходится.
Доказательство. Рассмотрим вспомогательный ряд
(u1+│u1│)+(u2+│u2│)+…+(un+│un│)+…=  (un+│un│). (22)
Очевидно, 0≤ un+│un│≤2│un│ при всех n=1, 2, … . Ряд (21) сходится по условию, поэтому сходится ряд
(un+│un│). (22)
Очевидно, 0≤ un+│un│≤2│un│ при всех n=1, 2, … . Ряд (21) сходится по условию, поэтому сходится ряд  2│un│, тогда по признаку сравнения сходится ряд (22). Ряд (20) представляет собой разность двух сходящихся рядов (22) и (21), поэтому он тоже сходится. Теорема доказана.
Замечание.
Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться.
Например, ряд
2│un│, тогда по признаку сравнения сходится ряд (22). Ряд (20) представляет собой разность двух сходящихся рядов (22) и (21), поэтому он тоже сходится. Теорема доказана.
Замечание.
Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться.
Например, ряд 
 сходится по признаку Лейбница, а ряд
сходится по признаку Лейбница, а ряд 
 расходится (это гармонический ряд).
Остаток ряда и его оценка
Рассмотрим сходящийся числовой ряд
расходится (это гармонический ряд).
Остаток ряда и его оценка
Рассмотрим сходящийся числовой ряд
 (23)
Вычисление суммы ряда S=
(23)
Вычисление суммы ряда S=  обычно технически очень сложно. Поэтому в качестве S берут S≈Sn. Точность этого равенства возрастает с увеличением n.
Определение 7. Если числовой ряд сходится, то разность Rn=S-Sn называется n-м остатком ряда.
Таким образом, Rn представляет собой сходящийся числовой ряд:
Rn= un+1+un+2+… .
Заметим, что
обычно технически очень сложно. Поэтому в качестве S берут S≈Sn. Точность этого равенства возрастает с увеличением n.
Определение 7. Если числовой ряд сходится, то разность Rn=S-Sn называется n-м остатком ряда.
Таким образом, Rn представляет собой сходящийся числовой ряд:
Rn= un+1+un+2+… .
Заметим, что  Rn=
Rn=  ( S-Sn)=S-S=0.
Абсолютная погрешность при замене суммы ряда S его частичной суммой Sn равна |Rn|=|S-Sn|. Таким образом, если требуется найти сумму ряда с точностью до E>0, то надо взять сумму такого числа nпервых членов ряда, чтобы выполнялось условие |Rn|<E. Однако в общем случае находить точно Rn не удаётся.
Теорема 11. (Об оценке остатка знакочередующегося числового ряда)
Если знакочередующийся числовой ряд сходится по признаку Лейбница, то его n-й остаток по абсолютной величине не превосходит модуля (n+1)-го члена ряда.
Доказательство. Пусть ряд u1-u2+u3-u4+…+(-1)n-1.un+… сходится по признаку Лейбница. Тогда n-й остаток ряда Rn=±(un+1-un+2+un+3-…) сам является суммой знакочередующегося числового ряда и по теореме Лейбница |Rn|≤|un+1|. Теорема доказана.
Пример.
Вычислить с точностью до 0,01 сумму ряда
( S-Sn)=S-S=0.
Абсолютная погрешность при замене суммы ряда S его частичной суммой Sn равна |Rn|=|S-Sn|. Таким образом, если требуется найти сумму ряда с точностью до E>0, то надо взять сумму такого числа nпервых членов ряда, чтобы выполнялось условие |Rn|<E. Однако в общем случае находить точно Rn не удаётся.
Теорема 11. (Об оценке остатка знакочередующегося числового ряда)
Если знакочередующийся числовой ряд сходится по признаку Лейбница, то его n-й остаток по абсолютной величине не превосходит модуля (n+1)-го члена ряда.
Доказательство. Пусть ряд u1-u2+u3-u4+…+(-1)n-1.un+… сходится по признаку Лейбница. Тогда n-й остаток ряда Rn=±(un+1-un+2+un+3-…) сам является суммой знакочередующегося числового ряда и по теореме Лейбница |Rn|≤|un+1|. Теорема доказана.
Пример.
Вычислить с точностью до 0,01 сумму ряда 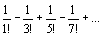 Очевидно, ряд сходится по признаку Лейбница. u1=
Очевидно, ряд сходится по признаку Лейбница. u1=  =1; u2=
=1; u2=  ≈ ≈0,166; u3=
≈ ≈0,166; u3=  ≈0,008<0,01. Поэтому S≈1-0,166≈0,84.
≈0,008<0,01. Поэтому S≈1-0,166≈0,84.
 , (24)
где a, a0, a1, a2, …, an, … – некоторые числа, называемые коэффициентами степенного ряда.
Теорема 12. (О структуре области сходимости степенного ряда)
Областью сходимости степенного ряда (24) является интервал (a-R;a+R), к которому в зависимости от конкретных случаев могут быть присоединены точки a-R и a+R, где R=
, (24)
где a, a0, a1, a2, …, an, … – некоторые числа, называемые коэффициентами степенного ряда.
Теорема 12. (О структуре области сходимости степенного ряда)
Областью сходимости степенного ряда (24) является интервал (a-R;a+R), к которому в зависимости от конкретных случаев могут быть присоединены точки a-R и a+R, где R=  (если этот предел существует). В каждой точке интервала (a-R;a+R) ряд сходится абсолютно.
Доказательство. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
|a0|+|a1|.|x-a|+|a2|.|x-a|2+…+|an|.|x-a|n+… (25)
Применим к ряду (25) признак Даламбера
(если этот предел существует). В каждой точке интервала (a-R;a+R) ряд сходится абсолютно.
Доказательство. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
|a0|+|a1|.|x-a|+|a2|.|x-a|2+…+|an|.|x-a|n+… (25)
Применим к ряду (25) признак Даламбера

 Возможны три случая:
1. Если
Возможны три случая:
1. Если  или |x-a|<R или xЄ(a-R;a+R), то ряд (25) сходится, но тогда по достаточному признаку сходимости знакопеременного ряда сходится и ряд (24), причём абсолютно.
2. Если
или |x-a|<R или xЄ(a-R;a+R), то ряд (25) сходится, но тогда по достаточному признаку сходимости знакопеременного ряда сходится и ряд (24), причём абсолютно.
2. Если  , то ряд (25) расходится. В этом случае
, то ряд (25) расходится. В этом случае  , то есть при достаточно больших n |un+1|>|un|, значит
, то есть при достаточно больших n |un+1|>|un|, значит  ≠0 и
≠0 и  ≠0, следовательно, ряд (24) расходится по следствию из необходимого признака сходимости. Теорема доказана.
Определение 14. Интервал (a-R;a+R), называется интервалом сходимости степенного ряда, а половина его длины R называется радиусом сходимости степенного ряда.
Замечание. Любой степенной ряд (24) сходится при x=a. Если других точек сходимости у ряда (24) нет, то считают, что R=0. Если степенной ряд (24) сходится во всех точках числовой прямой, то считают, что R=∞.
Примеры.
Найти область сходимости степенного ряда.
1.
≠0, следовательно, ряд (24) расходится по следствию из необходимого признака сходимости. Теорема доказана.
Определение 14. Интервал (a-R;a+R), называется интервалом сходимости степенного ряда, а половина его длины R называется радиусом сходимости степенного ряда.
Замечание. Любой степенной ряд (24) сходится при x=a. Если других точек сходимости у ряда (24) нет, то считают, что R=0. Если степенной ряд (24) сходится во всех точках числовой прямой, то считают, что R=∞.
Примеры.
Найти область сходимости степенного ряда.
1.  Составим ряд из абсолютных величин членов данного ряда
Составим ряд из абсолютных величин членов данного ряда  и применим к нему признак Даламбера. |un|=
и применим к нему признак Даламбера. |un|=  , |un+1|=
, |un+1|=  ,
,  = |x|.
= |x|.  |x|.
|x|.  |x|.
Ряд сходится, если |x|<1 или x
|x|.
Ряд сходится, если |x|<1 или x  (-1;1) – это и есть интервал сходимости. Исследуем концы этого интервала. При x=1 получаем расходящийся обобщённый гармонический ряд
(-1;1) – это и есть интервал сходимости. Исследуем концы этого интервала. При x=1 получаем расходящийся обобщённый гармонический ряд  . При x=-1 получаем знакочередующийся числовой ряд
. При x=-1 получаем знакочередующийся числовой ряд  сходящийся по признаку Лейбница.
Действительно,
сходящийся по признаку Лейбница.
Действительно,  =
=  и |un|=
и |un|=  |un+1|=
|un+1|=  Таким образом, областью сходимости данного ряда является промежуток [-1;1); R=1.
2.
Таким образом, областью сходимости данного ряда является промежуток [-1;1); R=1.
2.  Составим ряд из абсолютных величин членов данного ряда
Составим ряд из абсолютных величин членов данного ряда  и применим к нему признак Даламбера. |un|=n!.|x-a|n, |un+1|=(n+1)!.|x-a|n+1,
и применим к нему признак Даламбера. |un|=n!.|x-a|n, |un+1|=(n+1)!.|x-a|n+1, 
 =
=  Таким образом, областью сходимости данного ряда является одна точка x=a; R=0.
3.
Таким образом, областью сходимости данного ряда является одна точка x=a; R=0.
3.  Составим ряд из абсолютных величин членов данного ряда
Составим ряд из абсолютных величин членов данного ряда  и применим к нему признак Даламбера. |un|=
и применим к нему признак Даламбера. |un|=  |un+1|=
|un+1|= 

 при всех x. Таким образом, областью сходимости данного ряда является промежуток (-∞;+∞); R=∞.
Свойства степенных рядов
Отметим здесь без доказательства три важных свойства степенных рядов:
1. Сумма S(x) степенного ряда
S(x)=a0+a1(x-a)+a2(x-a)2+…+an(x-a)n+… (24)
является непрерывной функцией в каждой точке интервала сходимости (a-R;a+R).
2. Ряд
φ(x)=a1+2a2(x-a)+…+nan(x-a)n-1+…, (26)
полученный почленным дифференцированием ряда (24), является степенным рядом с тем же, что и ряд (24), интервалом сходимости (a-R;a+R). Сумма ряда (26) φ(x)=S'(x).
Замечание. Ряд (26) также можно почленно дифференцировать и сумма полученного после этого ряда равна
при всех x. Таким образом, областью сходимости данного ряда является промежуток (-∞;+∞); R=∞.
Свойства степенных рядов
Отметим здесь без доказательства три важных свойства степенных рядов:
1. Сумма S(x) степенного ряда
S(x)=a0+a1(x-a)+a2(x-a)2+…+an(x-a)n+… (24)
является непрерывной функцией в каждой точке интервала сходимости (a-R;a+R).
2. Ряд
φ(x)=a1+2a2(x-a)+…+nan(x-a)n-1+…, (26)
полученный почленным дифференцированием ряда (24), является степенным рядом с тем же, что и ряд (24), интервалом сходимости (a-R;a+R). Сумма ряда (26) φ(x)=S'(x).
Замечание. Ряд (26) также можно почленно дифференцировать и сумма полученного после этого ряда равна  и так далее. Таким образом, сумма
и так далее. Таким образом, сумма  ряда (24) является бесконечно дифференцируемой функцией в интервале сходимости
ряда (24) является бесконечно дифференцируемой функцией в интервале сходимости  . Сумма ряда, полученного из ряда (24) n-кратным дифференцированием равна
. Сумма ряда, полученного из ряда (24) n-кратным дифференцированием равна  Область сходимости степенного ряда при дифференцируемости не меняется.
3. Пусть числа
Область сходимости степенного ряда при дифференцируемости не меняется.
3. Пусть числа  и
и  принадлежат интервалу сходимости
принадлежат интервалу сходимости 
 ряда (24). Тогда имеет место равенство
ряда (24). Тогда имеет место равенство

 a2=
a2=  , a3=
, a3=  , …, an=
, …, an=  , … . Подставляя полученные значения коэффициентов в ряд (27), получаем
f(x)=f(a)+
, … . Подставляя полученные значения коэффициентов в ряд (27), получаем
f(x)=f(a)+  (x-a)+
(x-a)+  (x-a)2+…+
(x-a)2+…+  (x-a)n+… . (28)
ряд (28) называется рядом Тейлора для функции f(x) в точке a. В частном случае при a=0 ряд (28) принимает вид
f(x)=f(0)+
(x-a)n+… . (28)
ряд (28) называется рядом Тейлора для функции f(x) в точке a. В частном случае при a=0 ряд (28) принимает вид
f(x)=f(0)+ 
 +…+
+…+  +… (29)
и называется рядом Маклорена.
Таким образом, если функция f(x) является суммой степенного ряда, то этот ряд называется рядом Тейлора для функции f(x).
Пусть теперь дана бесконечно дифференцируемая в точке a функция f(x). Составим для неё формально ряд Тейлора:
f(a)+
+… (29)
и называется рядом Маклорена.
Таким образом, если функция f(x) является суммой степенного ряда, то этот ряд называется рядом Тейлора для функции f(x).
Пусть теперь дана бесконечно дифференцируемая в точке a функция f(x). Составим для неё формально ряд Тейлора:
f(a)+  +…+
+…+  +… .
Совпадает ли сумма полученного ряда Тейлора с функцией f(x), для которой он составлен? Оказывается, не всегда. При каких условиях сумма ряда Тейлора совпадает с функцией, для которой он составлен? Рассмотрим n-ю частичную сумму ряда Тейлора
Sn(x)= f(a)+
+… .
Совпадает ли сумма полученного ряда Тейлора с функцией f(x), для которой он составлен? Оказывается, не всегда. При каких условиях сумма ряда Тейлора совпадает с функцией, для которой он составлен? Рассмотрим n-ю частичную сумму ряда Тейлора
Sn(x)= f(a)+  +…+
+…+  . (30)
Многочлен (30) называется многочленом Тейлора степени n. Разность Rn(x)=f(x)-Sn(x) называется остаточным членом ряда Тейлора. Приведём без доказательства следующую теорему.
Теорема 13.
Для того, чтобы бесконечно дифференцируемая в точке а функция f(x) являлась суммой составленного для неё ряда Тейлора, необходимо и достаточно, чтобы
. (30)
Многочлен (30) называется многочленом Тейлора степени n. Разность Rn(x)=f(x)-Sn(x) называется остаточным членом ряда Тейлора. Приведём без доказательства следующую теорему.
Теорема 13.
Для того, чтобы бесконечно дифференцируемая в точке а функция f(x) являлась суммой составленного для неё ряда Тейлора, необходимо и достаточно, чтобы  Rn(x)=0.
Можно показать, что остаточный член можно представить в форме Лагранжа: Rn(x)=
Rn(x)=0.
Можно показать, что остаточный член можно представить в форме Лагранжа: Rn(x)= 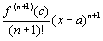 , где с – некоторое число из интервала (a;x). Таким образом
f(x)= f(a)+
, где с – некоторое число из интервала (a;x). Таким образом
f(x)= f(a)+  +…+
+…+  +
+  31)
Формула (31) называется формулой Тейлора, а её частный случай при а=0 называется формулой Маклорена:
f(x)= f(0)+
31)
Формула (31) называется формулой Тейлора, а её частный случай при а=0 называется формулой Маклорена:
f(x)= f(0)+  +…+
+…+  +
+ 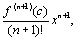 где с
где с  (0;x).
(0;x).
 .
Найдём области сходимости этого ряда.
.
Найдём области сходимости этого ряда.
 при любых x, следовательно, областью сходимости ряда является промежуток (-∞;+∞). Заметим, что так как ряд сходится абсолютно, то
при любых x, следовательно, областью сходимости ряда является промежуток (-∞;+∞). Заметим, что так как ряд сходится абсолютно, то  при любых хи тем более
при любых хи тем более  при любых х. Так как f(n+1)(x)=ex и f(n+1)(с)=eс, то
при любых х. Так как f(n+1)(x)=ex и f(n+1)(с)=eс, то 
 =ec
=ec  =0. Таким образом, имеет место разложение при x
=0. Таким образом, имеет место разложение при x  (-∞;+∞)
ex=1+
(-∞;+∞)
ex=1+  . (32)
2. Разложение функции f(x)=sinx в ряд Маклорена.
Вычислим производные данной функции.
f′(x)=cosx=sin(x+
. (32)
2. Разложение функции f(x)=sinx в ряд Маклорена.
Вычислим производные данной функции.
f′(x)=cosx=sin(x+  ), f″(x)=-sinx=sin(x+
), f″(x)=-sinx=sin(x+  ),
f″′(x)=-cosx=sin(x+
),
f″′(x)=-cosx=sin(x+  ), f(4)(x)=sinx=sin(x+
), f(4)(x)=sinx=sin(x+  ), …, f(n)(x)=sin(x+
), …, f(n)(x)=sin(x+  ), … . Вычислим значения f(x) и производных в точке 0: f(0)=0, f′(0)=1, f″(0)=0, f″′(0)=-1, f(4)(0)=0, …, f(2n-1)(0)=(-1)n-1,f(2n)(0)=0.
Исследуем остаточный член ряда.
|Rn(x)|= =
), … . Вычислим значения f(x) и производных в точке 0: f(0)=0, f′(0)=1, f″(0)=0, f″′(0)=-1, f(4)(0)=0, …, f(2n-1)(0)=(-1)n-1,f(2n)(0)=0.
Исследуем остаточный член ряда.
|Rn(x)|= =  так как |sin(c+(n+1)
так как |sin(c+(n+1)  |≤1. Переходя к пределу при n→∞, получаем
|≤1. Переходя к пределу при n→∞, получаем  следовательно,
следовательно,  и
и  . Рекомендуем показать самостоятельно, что областью сходимости ряда является промежуток (-∞;+∞). Таким образом, имеет место разложение при x
. Рекомендуем показать самостоятельно, что областью сходимости ряда является промежуток (-∞;+∞). Таким образом, имеет место разложение при x  (-∞;+∞):
sinx=x-
(-∞;+∞):
sinx=x-  . (33)
3. Разложение функции y=cosx в ряд Маклорена. Дифференцируя ряд (33), получаем разложение при x
. (33)
3. Разложение функции y=cosx в ряд Маклорена. Дифференцируя ряд (33), получаем разложение при x  (-∞;+∞):
cosx=1-
(-∞;+∞):
cosx=1-  . (34)
4. Биномиальный ряд.
Разложим в ряд Маклорена функцию f(x)=(1+x)m, где m≠0 – любое действительное число. Для этого вычислим производные: f′(x)=m(1+x)m-1, f″(x)=(m-1)m(1+x)m-2, f″′(x)=(m-2)(m-1)m(1+x)m-3, …, f(n)(x)=(m-n+1)…(m-2).(m-1)m(1+x)m-n, … При x=0 получаем f(0)=1, f′(0)=m, f″(0)=(m-1)m, f″′(0)=(m--2)(m-1)m, …, f(n)(0)=(m-n+1)…(m-2)(m-1)m, … .
Можно показать, что областью сходимости ряда является промежуток (-1;1) (на концах интервала ряд сходится или расходится в зависимости от конкретных значений m) и что
. (34)
4. Биномиальный ряд.
Разложим в ряд Маклорена функцию f(x)=(1+x)m, где m≠0 – любое действительное число. Для этого вычислим производные: f′(x)=m(1+x)m-1, f″(x)=(m-1)m(1+x)m-2, f″′(x)=(m-2)(m-1)m(1+x)m-3, …, f(n)(x)=(m-n+1)…(m-2).(m-1)m(1+x)m-n, … При x=0 получаем f(0)=1, f′(0)=m, f″(0)=(m-1)m, f″′(0)=(m--2)(m-1)m, …, f(n)(0)=(m-n+1)…(m-2)(m-1)m, … .
Можно показать, что областью сходимости ряда является промежуток (-1;1) (на концах интервала ряд сходится или расходится в зависимости от конкретных значений m) и что  . Таким образом, при x
. Таким образом, при x  (-1;1) имеет место разложение:
(1+x)m=1+
(-1;1) имеет место разложение:
(1+x)m=1+  +
+  +
+  +
+…+
+
+…+  . (35)
Ряд (35) называется биномиальным рядом.
5. Разложение функции f(x)=lnx в ряд Тейлора. При x=0 функция f(x)=lnx не определена, поэтому её нельзя разложить в ряд Маклорена. Разложим её в ряд Тейлора, например, по степеням (x-1). Для этого, вычислим производные: f′(x)=x-1, f″(x)=-1.x-2=-1!x-2, f″′(x)=1.2.x-3=2!x-3, f(4)(x)=-1.2. .3.x-4=-3!x-4, …, f(n)(x)=(-1)n-1. .(n-1)!x-n, … .
При x=1 получаем: f(1)=0, f′(1)=1, f″(1)=-1!, f″′(1)=2!, f(4)(1)=-3!, …, f(n)(1)=(-1)n-1(n-1)!, … .
Можно показать, что областью сходимости ряда является промежуток (0;2] и что
. (35)
Ряд (35) называется биномиальным рядом.
5. Разложение функции f(x)=lnx в ряд Тейлора. При x=0 функция f(x)=lnx не определена, поэтому её нельзя разложить в ряд Маклорена. Разложим её в ряд Тейлора, например, по степеням (x-1). Для этого, вычислим производные: f′(x)=x-1, f″(x)=-1.x-2=-1!x-2, f″′(x)=1.2.x-3=2!x-3, f(4)(x)=-1.2. .3.x-4=-3!x-4, …, f(n)(x)=(-1)n-1. .(n-1)!x-n, … .
При x=1 получаем: f(1)=0, f′(1)=1, f″(1)=-1!, f″′(1)=2!, f(4)(1)=-3!, …, f(n)(1)=(-1)n-1(n-1)!, … .
Можно показать, что областью сходимости ряда является промежуток (0;2] и что  . Таким образом, при x
. Таким образом, при x  (0;2] имеет место разложение:
lnx=
(0;2] имеет место разложение:
lnx=  . (36)
Заметим, что разложение функций в ряды Тейлора или Маклорена непосредственно часто связано с громоздкими вычислениями при нахождении производных и исследовании остаточного члена. На примерах покажем некоторые приёмы, позволяющие избежать этих трудностей.
Примеры.
1. Разложить в степенной ряд функцию
. (36)
Заметим, что разложение функций в ряды Тейлора или Маклорена непосредственно часто связано с громоздкими вычислениями при нахождении производных и исследовании остаточного члена. На примерах покажем некоторые приёмы, позволяющие избежать этих трудностей.
Примеры.
1. Разложить в степенной ряд функцию  .
В формуле (32) сделаем замену переменной x=-t2, получим
.
В формуле (32) сделаем замену переменной x=-t2, получим
 при t
при t  (-∞;+∞). Переобозначая t на x, получим нужное разложение:
(-∞;+∞). Переобозначая t на x, получим нужное разложение:
 при x
при x  (-∞;+∞).
2. Разложить в степенной ряд функцию f(x)=
(-∞;+∞).
2. Разложить в степенной ряд функцию f(x)=  .
Очевидно, f(x)=
.
Очевидно, f(x)=  . Обозначим x2=t и воспользуемся биноминальным рядом при m=-1.
. Обозначим x2=t и воспользуемся биноминальным рядом при m=-1.
 =
= 
 =1-t+t2-t3+…+(-1)n.tn+… , t
=1-t+t2-t3+…+(-1)n.tn+… , t  (-1;1). (37)
Возвращаясь к переменной x, получаем разложение при x
(-1;1). (37)
Возвращаясь к переменной x, получаем разложение при x  (-1;1):
(-1;1):
 =1-x2+x4-x6+…+(-1)n.x2n+… . (38)
3. Разложить в ряд Маклорена функцию f(x)=ln(1+x).
Проинтегрируем обе части равенства (37) от 0 до x при x
=1-x2+x4-x6+…+(-1)n.x2n+… . (38)
3. Разложить в ряд Маклорена функцию f(x)=ln(1+x).
Проинтегрируем обе части равенства (37) от 0 до x при x  (-1;1). Получим
(-1;1). Получим
 или
ln(1+x)=x
или
ln(1+x)=x  . (39)
Можно показать, что ряд (39) имеет область сходимости (-1;1].
4. Разложить в степенной ряд функцию f(x)=arctgx.
Проинтегрируем обе части равенства (38) от 0 до x при x
. (39)
Можно показать, что ряд (39) имеет область сходимости (-1;1].
4. Разложить в степенной ряд функцию f(x)=arctgx.
Проинтегрируем обе части равенства (38) от 0 до x при x  (-1;1):
(-1;1):
 или
arctgx=x
или
arctgx=x 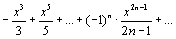 . (40)
Можно показать, что ряд (40) имеет область сходимости [-1;1].
. (40)
Можно показать, что ряд (40) имеет область сходимости [-1;1].
 с точностью до 0,001.
Воспользуемся разложением
с точностью до 0,001.
Воспользуемся разложением  Тогда
Тогда
 =
= 


 0,0238+0,0046– –0,0008≈0,7475≈0,748.
Так как ряд знакочередующийся и 0,0008<0,001, то все слагаемые, начиная с 0,0008, отбрасываем и при этом погрешность не превосходит 0,001.
Пример 2.
Вычислить
0,0238+0,0046– –0,0008≈0,7475≈0,748.
Так как ряд знакочередующийся и 0,0008<0,001, то все слагаемые, начиная с 0,0008, отбрасываем и при этом погрешность не превосходит 0,001.
Пример 2.
Вычислить  с точностью до 0,001.
с точностью до 0,001.
 =
=  Используем биномиальный ряд при x=0.25; m=
Используем биномиальный ряд при x=0.25; m= 
 ≈2(1+
≈2(1+  +
+  2.(1+0,0833--0,0069+0,00096) ≈ ≈2.(1+0,0833-0,0069) ≈2,1528≈2,153.
Так как, начиная со второго члена, ряд знакочередующийся и 0,00096<0,001, то все слагаемые, начиная с 0,00096, отбрасываем и при этом погрешность не превосходит 0,001.
Пример 3.
Вычислить e0,1 с точностью до 0,001.
Для функции ex формула Тейлора имеет вид: ex=1+x+
2.(1+0,0833--0,0069+0,00096) ≈ ≈2.(1+0,0833-0,0069) ≈2,1528≈2,153.
Так как, начиная со второго члена, ряд знакочередующийся и 0,00096<0,001, то все слагаемые, начиная с 0,00096, отбрасываем и при этом погрешность не превосходит 0,001.
Пример 3.
Вычислить e0,1 с точностью до 0,001.
Для функции ex формула Тейлора имеет вид: ex=1+x+ 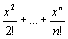 +Rn(x), где Rn(x)=
+Rn(x), где Rn(x)=  где с
где с  (0;x).
При x=0.1 получаем знакоположительный числовой ряд. Так как при этом с
(0;x).
При x=0.1 получаем знакоположительный числовой ряд. Так как при этом с  (0;0,1), 0,1
(0;0,1), 0,1  [0;0,5], то 0<c<0,1<0,5 и ec<e0,5<2. Тогда
[0;0,5], то 0<c<0,1<0,5 и ec<e0,5<2. Тогда  Необходимо взять столько членов ряда, чтобы выполнялось условие:
Необходимо взять столько членов ряда, чтобы выполнялось условие:  0,001 или
0,001 или  0,0005.
При x=0,1 получаем
e0,1≈1+0,1+
0,0005.
При x=0,1 получаем
e0,1≈1+0,1+  ≈1+0,1+0,005+0,0002≈1,1052≈1,105.
Так как 0,0002<0,0005, то достаточно взять четыре члена ряда.
Пример 4.
Проинтегрировать дифференциальное уравнение y′=y+x2, y(0)=-2 методом последовательного дифференцирования.
Будем искать решение в виде ряда Маклорена:
y(x)=y(0)+
≈1+0,1+0,005+0,0002≈1,1052≈1,105.
Так как 0,0002<0,0005, то достаточно взять четыре члена ряда.
Пример 4.
Проинтегрировать дифференциальное уравнение y′=y+x2, y(0)=-2 методом последовательного дифференцирования.
Будем искать решение в виде ряда Маклорена:
y(x)=y(0)+  .
Вычислим производные: y′=y+x2, y″=y′+2x, y″′=y″+2, y(4)= y″′, …, y(n)= y″′ при n=4, 5, … .
При x=0 получаем: y(0)=-2, y′(0)=-2, y″(0)=-2, y(n)(0)=0 при n=3, 4, 5. Окончательно получаем y(x)=-2-2x-x2.
.
Вычислим производные: y′=y+x2, y″=y′+2x, y″′=y″+2, y(4)= y″′, …, y(n)= y″′ при n=4, 5, … .
При x=0 получаем: y(0)=-2, y′(0)=-2, y″(0)=-2, y(n)(0)=0 при n=3, 4, 5. Окончательно получаем y(x)=-2-2x-x2.
