 |
|
Тема: Регресивний аналіз поштового наватаження в УДППЗ «Укрпошта»
У практичних дослідженнях виникає необхідність апроксимувати (описати приблизно) діаграму розсіяння математичним рівнянням. Тобто залежність між змінними величинами Y і Х можна виразити аналітично за допомогою формул і рівнянь і графічно у вигляді геометричного місця крапок в системі прямокутних координат. Графік кореляційної залежності будується по рівняннях функції 
і 
, які називаються регресією (термін “регресія” походить від латів. regressio — рух назад). Тут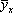 
і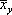 
— середні арифметичні з числових значень залежних змінних Y і X.
Для вираження регресії служать емпіричні і теоретичні ряди, їх графіки — лінії регресії, а також кореляційні рівняння (рівняння регресії) і коефіцієнт лінійної регресії. Показники регресії виражають кореляційний зв'язок двосторонньо, враховуючи зміну середньої величини ознаки Y при зміні значень xi прізнака X, і навпаки, показують зміну середньої величини 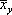ознаки Х по змінених значеннях yi ознаки Y. Виняток становлять тимчасові ряди, або ряди динаміки, що показують зміну ознак в часі.
Регресія таких рядів є однобічною. Ряди регресії, особливо їх графіки, дають наочне уявлення про форму і тісноту кореляційного зв'язку між ознаками, в чому і полягає їх цінність. Форма зв'язку між показниками, що впливають на рівень спортивного результату і загальної фізичної підготовки що займаються фізичною культурою і спортом, може бути всілякою. І тому завдання полягає в тому, щоб будь-яку форму кореляційного зв'язку виразити рівнянням певної функції (лінійною графіки, дають наочне уявлення про форму і тісноту кореляційною, параболічною і так далі), що дозволяє отримувати потрібну інформацію про кореляцію між змінними велічинаміy і X, передбачати можливі зміни ознаки Y на основі відомих змін X, пов'язаного з Y кореляційно.
Парна регресія-рівняння зв'язку два змінних y і х:
де:
y - залежна змінна (результативна ознака – обміну письмової коріспонденциї за 2009 рік, тис ед.);
x - незалежна, пояснююча змінна (ознака - (чинник) кількості автомобілів)
Лінійна регресія: 
Нелінійні регресії діляться на два класи: регресії, нелінійні відносно включених в аналіз пояснюючих змінних, але лінійні по оцінюваних параметрах, і регресії, нелінійні по оцінюваних параметрах.
Регрессии, нелинейные по объясняющим переменным:
- полиномы разных степеней
- рівностороння гіпербола 
.
Регресії, нелінійні по оцінюваних параметрах:
- степенна 
- показова 
- експоненціальна 
Побудова рівняння регресії зводиться до оцінки її параметрів. Для оцінки параметрів регресій, лінійних по параметрах, Використовують метод найменших квадратів (МНК). МНК дозволяє отримати такі оцінки параметрів, при яких сума квадратів відхилень фактичних значень результативної ознаки у від теоретичних 
мінімальна, тобто 
.
Для лінійних і нелінійних рівнянь, що приводяться до лінійних, вирішується наступна система відносно а і b:
Можна скористатися готовими формулами, які витікають з цієї системи:
Тісноту зв'язку явищ, що вивчаються, оцінює лінійний коефіцієнт парної кореляції 
для лінійної регресії 
:
і індекс кореляції 
- для нелінійної регресії : 
:
Оцінку якості побудованої моделі дасть коефіцієнт (індекс) детермінації, а також середня помилка апроксимації. Середня помилка апроксимації - середнє відхилення розрахункових значень від фактичних:
.
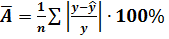Допустима межа значень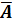 
- не більше 8-10%.
Середній коефіцієнт еластичності 
показує, на скільки відсотків в середньому по сукупності зміниться результат у від своєї середньої величини при зміні чинника x на 1% від свого середнього значення:
.
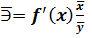Завдання дисперсійного аналізу полягає в аналізі дисперсії залежною змінною:
,
где 
- загальна сума квадратів відхилень;
- сума квадратів відхилень, обумовлена регресією («пояснена» або «факторна»);
- залишкова сума квадратів відхилень.
Долю дисперсії, з'ясовну регресією, в загальній дисперсії результативної ознаки в характеризує коефіцієнт (індекс) детерміації 
:
Коефіцієнт детерміації - квадрат коефіцієнта або індексу кореляції.
F-тест - оцінювання якості рівняння регресії - полягає в перевірці гіпотези Но про статистичну незначущість рівняння регресії і показника тісноти зв'язку. Для цього виконується порівняння фактичного Fфакт і критичного (табличного) Fтабл значень F -крітерію Фішера.
Нулевая гипотеза (Но) — это гипотеза о том, что есть две совокупности, которые сравниваются по одному или нескольким признакам, не отличаются. При этом предполагают, что действительное различие сравниваемых величин равно нулю, а выявленное по данным отличие от нуля несет случайный характер. Нулевая гипотеза отвергается в тех случаях, когда по выборке получается результат, который при истинности выдвинутой нулевой гипотезы маловероятен. Границей маловероятного или невозможного обычно считают а = 0,05 или 0,01; 0,001.
Критерий Фишера применяется для проверки равенства дисперсий двух выборок. Его относят к критериям рассеяния.
При проверке гипотезы положения (гипотезы о равенстве средних значений в двух выборках) с использованием критерия Стьюдента имеет смысл предварительно проверить гипотезу о равенстве дисперсий. Если она верна, то для сравнения средних можно воспользоваться более мощным критерием.
В регрессионном анализе критерий Фишера позволяет оценивать значимость линейных регрессионных моделей. В частности, он используется в шаговой регрессии для проверки целесообразности включения или исключения независимых переменных (признаков) в регрессионную модель.
В дисперсионном анализе критерий Фишера позволяет оценивать значимость факторов и их взаимодействия.
Критерий Фишера основан на дополнительных предположениях о независимости и нормальности выборок данных. Перед его применением рекомендуется выполнить проверку нормальности.
F - критерий Фишера является параметричесикм критерием и используется для сравнения дисперсий двух вариационных рядов. Эмпирическое значение критерия вычисляется по формуле:
,
, 
где - большая дисперсия, - меньшая дисперсия рассматриваемых вариационных рядов.
Если вычисленное значение критерия Fэмп больше критического для определенного уровня значимости и соответствующих чисел степеней свободы для числителя и знаменателя, то дисперсии считаются различными. Иными словами, проверяется гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: H0={Dx=Dy}.
Критическое значение критерия Фишера следует определять по специальной таблице, исходя из уровня значимости α и степеней свободы числителя (n1-1) и знаменателя (n2-1).
Проиллюстрируем применение критерия Фишера на следующем примере. Дисперсия такого показателя, как стрессоустойчивость для учителей составила 6,17 (n1=32), а для менеджеров 4,41 (n2=33). Определим, можно ли считать уровень дисперсий примерно одинаковым для данных выборок на уровне значимости 0,05.
Для ответа на поставленный вопрос определим эмпирическое значение критерия: 
.При этом критическое значение критерия Fкр(0,05;31;32)=2.
Таким образом, Fэмп=1,4<2=Fкр, поэтому нулевая гипотеза о равенстве генеральных дисперсий на уровне значимости 0,05 принимается.
Непараметрические критерии
Непараметрические критерии не содержат расчёта параметров распределения и основаны на оперировании частотами или рангами. Непараметрические критерии, как правило, менее сложны в вычислениях и могут быть измерены в любой шкале, начиная от шкалы наименований.
Fфакт визначається із співвідношення значень факторної і залишкової дисперсій, розрахованих на одну міру свободи:
,
де n - число одиниць сукупності;
m - число параметрів при змінних х.
Fтабл - це максимально можливе значення критерію під впливом випадкових чинників при даних мірах свободи і рівні значущості а. Рівень значущості а - вірогідність відкинути правильну гіпотезу за умови, що вона вірна. Зазвичай а приймається рівною 0,05 або 0,01. Якщо Fтабл > Fфакт, то Но - гіпотеза про випадкову природу оцінюваних характеристик відхиляється і признається їх статистична значущість і надійність. Якщо Fтабл > Fфакт, то гіпотеза Но не відхиляється і признається статистична незначущість, ненадійність рівняння регресії. Для оцінки статистичної значущості коефіцієнтів регресії і кореляції розраховуються t-крітерій Стьюдента і довірительні інтервали кожного з показників. Висувається гіпотеза Но про випадкову природу показників, тобто про незначиму їх відмінність від нуля. Оцінка значущості коефіцієнтів регресії і кореляції за допомогою t-крітерію Стьюдента проводиться шляхом зіставлення їх значень з величиною випадкової помилки:
; 
; 
.
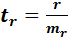Випадкові помилки параметрів лінійної регресії і коефіцієнта кореляції визначаються по формулах:
Порівнюючи фактичне і критичне (табличне) значення t-статистики - tтабл і tфакт - приймаємо або відкидаємо гіпотезу Але. Зв'язок між f-крітерієм Фішера і t-статістікою Стьюдента виражається рівністю
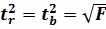
Якщо tтабл < tфакт те Ho відхиляється, тобто а, b і не випадково відрізняються від нуля і сформувалися під впливом систематично діючих чинника х. Якщо tтабл > tфакт те гіпотеза Но не відхиляється і признається випадкова природа формування а, b або .
Для розрахунку довірчого інтервалу визначаємо граничну помилку D для кожного показника:
, 
.
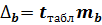Формулы для расчета доверительных интервалов имеют следующий вид:
; 
; 
; 
; 
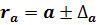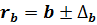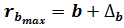
Якщо в кордони довірчого інтервалу потрапляє нуль, тобто нижній кордон негативний, а верхня позитивна, то оцінюваний параметр приймається нульовим, оскільки він не може одночасно набувати і позитивного, і негативного значень.
Прогнозне значення визначається шляхом підстановки в рівняння регресії 
відповідного (прогнозного) значення 
. Обчислюється середня стандартна помилка прогнозу 
:
,
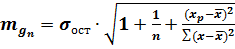где 
і будується довірчий інтервал прогнозу:
; 
; 
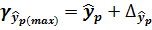
где 
.
Приклад аналізу обміну письмової кореспонденції в УДППЗ “Укрпочта”
Приклад розрахунку регрессивного аналізу обміну письмової кореспонденції в УДППЗ “Укрпочта”
Таблица 1.
| № | Область | Посилки звичайні, масою 10 кг без оголошеної цінності(тис.од) за 2008 | Кількість транспорту (автомобілів) |
| Вінницька | 80,2 | ||
| Волинська | 49,9 | ||
| Дніпропетровська | 162,5 | ||
| Донецька | 250,4 | ||
| Житомирська | 49,5 | ||
| Закарпатська | 30,4 | ||
| Запорізька | 86,5 | ||
| Ів-Франківська | 55,6 | ||
| Київська обласна | 27,4 | ||
| Кіровоградська | 35,4 | ||
| Кримська | 186,6 | ||
| Луганська | 87,9 | ||
| Львівська | 132,5 | ||
| Миколаївська | 20,3 | ||
| Одеська | 141,1 | ||
| Полтавська | 107,4 | ||
| Рівненська | 35,4 | ||
| Сумська | 47,9 | ||
| Тернопільська | 22,3 | ||
| Харківська | 148,4 | ||
| Херсонська | 59,6 | ||
| Хмельницька | 40,0 | ||
| Черкаська | 64,7 | ||
| Чернігівська | 64,6 | ||
| Чернівецька | 54,2 | ||
| Севастопольська | 21,0 |
Для розрахунку двух змінних х і у потрібно:
1. Для характеристики залежності у від х розрахувати параметри наступних функцій:
а) лінійною;
б) статечною (заздалегідь потрібно виробити процедуру лінеаризації змінних, шляхом логарифмування обох частин);
у) показовою; г) рівносторонньої гіперболи (так само потрібно придумати як заздалегідь лінеарізовать дану модель).
2. Оцінити кожну модель через середню помилку апроксимації і f-крітерій Фішера.
Приклад розрахунку
la. Для розрахунку параметрів а і b лінійної регресії 
вирішуем систему нормальних рівнянь відносно а і b:
За вихідними даними розраховуємо 
:
Таблица 1.1
| y | x | yx | x2 | y2 |  
| Аі | ||
| Вінницька | 80,2 | 13714,20 | 29241,00 | 6432,04 | -76,73 | 156,93 | 1,96 | |
| Волинська | 49,9 | 6487,00 | 16900,00 | 2490,01 | -48,10 | 98,00 | 1,96 | |
| Дніпропетровська | 162,5 | 39000,00 | 57600,00 | 26406,25 | -154,50 | 317,00 | 1,95 | |
| Донецька | 250,4 | 49829,60 | 39601,00 | 62700,16 | -237,57 | 487,97 | 1,95 | |
| Житомирська | 49,5 | 6286,50 | 16129,00 | 2450,25 | -47,72 | 97,22 | 1,96 | |
| Закарпатська | 30,4 | 3161,60 | 10816,00 | 924,16 | -29,67 | 60,07 | 1,98 | |
| Запорізька | 86,5 | 15397,00 | 31684,00 | 7482,25 | -82,69 | 169,19 | 1,96 | |
| Ів-Франківська | 55,6 | 4892,80 | 7744,00 | 3091,36 | -53,49 | 109,09 | 1,96 | |
| Київська обласна | 27,4 | 4000,40 | 21316,00 | 750,76 | -26,84 | 54,24 | 1,98 | |
| Кіровоградська | 35,4 | 5557,80 | 24649,00 | 1253,16 | -34,40 | 69,80 | 1,97 | |
| Кримська | 186,6 | 47956,20 | 66049,00 | 34819,56 | -177,28 | 363,88 | 1,95 | |
| Луганська | 87,9 | 17140,50 | 38025,00 | 7726,41 | -84,01 | 171,91 | 1,96 | |
| Львівська | 132,5 | 28487,50 | 46225,00 | 17556,25 | -126,15 | 258,65 | 1,95 | |
| Миколаївська | 20,3 | 2070,60 | 10404,00 | 412,09 | -20,13 | 40,43 | 1,99 | |
| Одеська | 141,1 | 25821,30 | 33489,00 | 19909,21 | -134,28 | 275,38 | 1,95 | |
| Полтавська | 107,4 | 16754,40 | 24336,00 | 11534,76 | -102,44 | 209,84 | 1,95 | |
| Рівненська | 35,4 | 4035,60 | 12996,00 | 1253,16 | -34,40 | 69,80 | 1,97 | |
| Сумська | 47,9 | 7041,30 | 21609,00 | 2294,41 | -46,21 | 94,11 | 1,96 | |
| Тернопільська | 22,3 | 2341,50 | 11025,00 | 497,29 | -22,02 | 44,32 | 1,99 | |
| Харківська | 148,4 | 33983,60 | 52441,00 | 22022,56 | -141,18 | 289,58 | 1,95 | |
| Херсонська | 59,6 | 7807,60 | 17161,00 | 3552,16 | -57,27 | 116,87 | 1,96 | |
| Хмельницька | 40,0 | 4840,00 | 14641,00 | 1600,00 | -38,74 | 78,74 | 1,97 | |
| Черкаська | 64,7 | 10093,20 | 24336,00 | 4186,09 | -62,08 | 126,78 | 1,96 | |
| Чернігівська | 64,6 | 8398,00 | 16900,00 | 4173,16 | -61,99 | 126,59 | 1,96 | |
| Чернівецька | 54,2 | 3794,00 | 4900,00 | 2937,64 | -52,16 | 106,36 | 1,96 | |
| Севастопольська | 21,0 | 1239,00 | 3481,00 | 441,00 | -20,79 | 41,79 | 1,99 | |
| Київська міська | 1 238,4 | 13622,40 | 121,00 | 1533634,56 | -1171,20 | 2409,60 | 1,95 | |
| Итого | 3300,1 | 3921,0 | 383753,6 | 653819,0 | 1782530,7 | -3144,0 | 6444,1 | 53,01 |
| Ср значение | 126,9 | 230,6 | 14759,8 | 25146,9 | 68558,9 | -120,9 | 247,9 | 1,96 |
| s | 95,06 | 123,94 | ||||||
| s2 | 9036,44 | 15360,81 |
Ι
Для розрахунку таблиці 1.1, потрібно:
1) Вихідні значення х і у перемножити,возвести до квадрату;
2) Визначити торбу кожного стовпця;
3) Визначити середнє значення (суму/кількість ), 
, 
, 
, 
, 
;
4)Визначити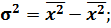 
5) Для визначення σ потрібно визначити корінь з 
;
6) Для розрахунку параметрів а і b лінійної регресії Використовуваний наступні формули:
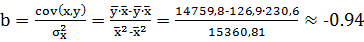
Уравнение регрессии: у = 344,88- 0,94х.
С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,94 %-ных пункта.
Рассчитаем линейный коэффициент парной корреляции:
Связь умеренная, обратная.
Определим коэффициент детерминации:
Вариация результата объясняется вариацией фактора х. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения . Найдем величину средней ошибки аппроксимации :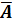
В среднем расчетные значения отклоняются от фактических на 2 %.
Рассчитаем F-критерий:
поскольку 1< F <¥, следует рассмотреть F -1.
Полученное значение указывает на необходимость принять гипотезу Но о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.