Главная | Обратная связь

Необходимый теоретический материал.

ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА

Методические указания

 

Иркутск 2008

Оглавление

 

	Ведение……………………………………………………………………
§1	Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными…………………………………………………………………………
	1.1. Необходимый теоретический материал………………………..
	1.2. Пример выполнения задачи1 (приведение к каноническому виду уравнений гиперболического типа) ...
	1.3. Пример выполнения задачи 2 (приведение к каноническому виду уравнений параболического типа)
	1.4. Пример выполнения задачи 3 (приведение к каноническому виду уравнений эллиптического типа) ..
	1.5. Задачи для самостоятельного решения ………………….….
§2	Упрощение группы младших производных для уравнений второго порядка с постоянными коэффициентами
	2.1. Необходимый теоретический материал …………………..
	2.2. Пример выполнения задачи 4
	2.3. Задачи для самостоятельного решения ……………………..

 

 

ВВЕДЕНИЕ

В настоящих методических указаниях изложен теоретический материал и на конкретных примерах разобрано приведение к каноническому виду линейных уравнений с частными производными второго порядка с двумя независимыми переменными для уравнений гиперболического, эллиптического и параболического типов.

Методические указания предназначены для студентов математических специальностей очной и заочной формы обучения.

 

Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными.

 

Задача. Определить тип уравнения

 

(1)

и привести его к каноническому виду.

Необходимый теоретический материал.

I. Тип уравнения (1) определяется знаком выражения :

· если в некоторой точке, то уравнение (1) называется уравнением гиперболического типа в этой точке;

· если в некоторой точке, то уравнение (1) называется уравнением эллиптического типа в этой точке;

· если в некоторой точке, то уравнение (1) называется уравнением параболического типа в этой точке.

Уравнение (1) будет являться уравнением гиперболического, эллиптического, параболического типа в области D, если оно гиперболично, эллиптично, параболично в каждой точке этой области.

Уравнение (1) может менять свой тип при переходе из одной точки (области) в другую. Например, уравнение является уравнением эллиптического типа в точках ; параболического типа в точках ; и гиперболического типа в точках .

II. Чтобы привести уравнение к канонического виду, необходимо:

1. Определить коэффициенты ;

2. Вычислить выражение ;

3. Сделать вывод о типе уравнения (1) (в зависимости от знака выражения );

4. Записать уравнение характеристик:

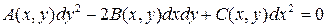; (2)

5. Решить уравнение (2). Для этого:

а) разрешить уравнение (2) как квадратное уравнение относительно dy:

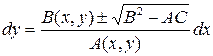; (3)

б) найти общие интегралы уравнений (3) (характеристики уравнения (1)):

· (4)

в случае уравнения гиперболического типа;

· , (5)

в случае уравнения параболического типа;

· , (6)

в случае уравнения эллиптического типа.

6. Ввести новые (характеристические) переменные и :

· в случае уравнения гиперболического типа в качестве и берут общие интегралы (4) уравнений (3), т.е.

· в случае уравнения параболического типа в качестве берут общий интеграл (5) уравнения (3), т.е. 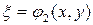, в качестве берут произвольную, дважды дифференцируемую функцию , не выражающуюся через , т.е. ;

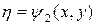· в случае уравнения эллиптического типа в качестве и берут вещественную и мнимую часть любого из общих интегралов (6) уравнений (3):

7. Пересчитать все производные, входящие в уравнение (1), используя правило дифференцирования сложной функции:

,

,

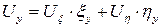, (7)

,

.

8. Подставить найденные производные в исходное уравнение (1) и привести подобные слагаемые. В результате уравнение (1) примет один из следующих видов:

· в случае уравнения гиперболического типа:

 

;

· в случае уравнения параболического типа:

 

;

· в случае уравнения эллиптического типа:

 

.