 |
|
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Генеральная (статистическая) совокупность– множество объектов одного и того же вида или множество значений какого-либо признака объекта.
Случайная выборка (просто выборка)– совокупность случайно отобранных объектов наблюдения из генеральной совокупности. Часто для исследования случайной величины (СВ) при постоянных условиях проводят испытания. Множество полученных значений также называют выборкой и обрабатывают ее статистически, т.е. определяют закон распределения, численные характеристики и пр.
Каждый отдельный объект выборки представляет собой элемент (единицу) совокупности, а общее число элементов – объем выборки. Объем генеральной совокупности обозначается  , объем выборки -
, объем выборки -  . Например, известны значения влажности досок в штабеле: 19,8; 17,4; 18,3; 19; 18,9 %. Здесь объем выборки
. Например, известны значения влажности досок в штабеле: 19,8; 17,4; 18,3; 19; 18,9 %. Здесь объем выборки  .
.
Каждой численной характеристике СВ соответствует ее статистическая аналогия, которая является только оценкойнеизвестного параметра генеральной совокупности. Оценка параметра – определенная численная характеристика, полученная на основе выборки.
Для математического ожидания такой аналогией является среднее арифметическое всех возможных значений СВ. Эту характеристику называют статистическим средним, выборочным средним или средним значением. Среднее значение – это обобщенный показатель, характеризующий типичный уровень явления. В средних величинах погашаются индивидуальные различия единиц совокупности.
При малом числе наблюдений среднее  наблюдаемых значений СВ определяется выражением:
наблюдаемых значений СВ определяется выражением:

Если математическое ожидание является характеристикой положения СВ, то дисперсия характеризует разброс, рассеянность значений СВ около ее математического ожидания. Слово «дисперсия» означает рассеивание. Аналогом дисперсии СВ является выборочная дисперсия. При малом числе наблюдаемых значений СВ вычисляют исправленную дисперсию
 при
при  <30.
<30.
В знаменателе формулы стоит (  -1) потому, что при малом объеме наблюдений среднее для выборки отличается от среднего генеральной совокупности. Здесь
-1) потому, что при малом объеме наблюдений среднее для выборки отличается от среднего генеральной совокупности. Здесь  =
=  -1 – число степеней свободы, так как при расчете среднего была наложена одна связь:
-1 – число степеней свободы, так как при расчете среднего была наложена одна связь: 
 .
.
Статистическим аналогом среднеквадратичного отклонения является стандартное отклонение 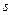 .
.
Статистической надежности в 95% соответствует доверительная вероятность – 0,95, а 5% задает уровень значимости  или вероятность ошибки 0,05. Обычно в статистике уровень значимости выбирают таким, чтобы он не превысил 5%, т.е.
или вероятность ошибки 0,05. Обычно в статистике уровень значимости выбирают таким, чтобы он не превысил 5%, т.е.  <0,05. Доверительная вероятность и уровень значимости дополняют друг друга до 1 (или 100%) и определяют надежность статистического высказывания.
<0,05. Доверительная вероятность и уровень значимости дополняют друг друга до 1 (или 100%) и определяют надежность статистического высказывания.
Законом распределения СВ называют всякое соотношение, устанавливающее связь между возможными значениями СВ и вероятностями этих значений.
В случае малых выборок вероятность появления больших отклонений значительно уменьшается. Поэтому классическая теория, основанная на нормальном законе распределения, при малых выборках неприменима. В этом случае используются другие законы распределения, разработанные микростатистикой: распределения Стьюдента и Фишера.
Эти распределения используются при формировании выборки из выборок малого объема и установлении статистической значимости случайных величин, параметров и уравнений.
Малая выборка содержит мало информации об интересующем свойстве. Для получения более надежных выводов требуется объединить малые выборки в одну, но при этом необходимо установить их однородность. Совокупности однородны, если равны их математические ожидания.
Критериями для сравнения выборок служат: равенство двух выборочных дисперсий, равенство двух выборочных средних и однородность ряда выборочных дисперсий.
Предпосылки дисперсионного анализа:
· серии наблюдений представляют собой случайные выборки из генеральных совокупностей, подчиняющихся нормальному закону распределения;
· дисперсии, связанные с ошибками измерений результативного признака, должны быть однородны.
Критерий однородности ряда дисперсий.Однородность дисперсий ошибок измерений случайной величины в случае равного объема выборок оценивают по критерию Кохрена, расчетное значение которого определяют по формуле
 ,
,
где  - дисперсия ошибок измерения СВ
- дисперсия ошибок измерения СВ  - й выборки;
- й выборки; 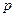 - число выборок.
- число выборок.
Критическое значение критерия Кохрена определяют по таблице 1 (приложение 2) при заданных значениях уровня значимости  и степенях свободы:
и степенях свободы: 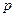 ;
;  , где
, где  - число измерений (объем выборки).
- число измерений (объем выборки).
Пример 1.При определении предела прочности получены следующие значения дисперсий ошибок измерений пяти партий бетона: 2,5; 2,8; 3,2; 2,4; 2,7. Ошибки во всех случаях подсчитывались по 17 – ти измерениям.
Оценить однородность дисперсий ошибок измерений прочности, т.е. возможность воспроизводимости опытов по определению прочности.
Определяем расчетное значение критерия
 =
=  =0,235.
=0,235.
Критическое значение критерия при 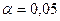 и
и  равно 0,3645. Таким образом,
равно 0,3645. Таким образом,  , гипотеза об однородности дисперсий ошибок измерений подтверждается с вероятностью 95 % и можно проводить дисперсионный анализ.
, гипотеза об однородности дисперсий ошибок измерений подтверждается с вероятностью 95 % и можно проводить дисперсионный анализ.
Критерий равенства двух дисперсий.Для сравнения дисперсий двух выборок используют  - критерий Фишера. Определяют расчетное значение
- критерий Фишера. Определяют расчетное значение  - критерия в виде отношения большей дисперсии к меньшей
- критерия в виде отношения большей дисперсии к меньшей
 .
.
Так как проверяется гипотеза о равенстве генеральных дисперсий, то желательно, чтобы это отношение было как можно ближе к единице. Критическое значение  - критерия вычисляем с помощью статистической функции
- критерия вычисляем с помощью статистической функции  РАСПОБР. Число степеней свободы принимают соответственно
РАСПОБР. Число степеней свободы принимают соответственно  , где
, где  - объем выборки. Гипотеза о равенстве дисперсий подтверждается, если
- объем выборки. Гипотеза о равенстве дисперсий подтверждается, если  .
.
Критерий равенства двух средних.Для сравнения двух выборочных средних используют 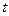 - статистику. После проверки гипотезы о равенстве двух выборочных дисперсий, вычисляют общую дисперсию двух выборок и расчетное значение
- статистику. После проверки гипотезы о равенстве двух выборочных дисперсий, вычисляют общую дисперсию двух выборок и расчетное значение 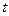 - статистики по формулам:
- статистики по формулам:
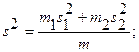

Критическое значение 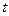 - статистики определяем с помощью статистической функции СТЬЮДРАСПОБР. Число степеней свободы
- статистики определяем с помощью статистической функции СТЬЮДРАСПОБР. Число степеней свободы  . Уровень значимости принимают в пределах 0,01-0,1. Гипотеза о равенстве выборочных средних подтверждается, если
. Уровень значимости принимают в пределах 0,01-0,1. Гипотеза о равенстве выборочных средних подтверждается, если  .
.
Пример 2. Сравним результаты испытаний двух выборок образцов бетона. В первой выборке объемом 29 образцов средний предел прочности  =40,1 МПа, дисперсия
=40,1 МПа, дисперсия  =8,2. Во второй выборке объемом 13 образцов средний предел прочности
=8,2. Во второй выборке объемом 13 образцов средний предел прочности  =40,9 МПа, дисперсия
=40,9 МПа, дисперсия  =7,1.
=7,1.
Расчетное значение  - критерия:
- критерия:
 =8,2/7,1=1,155.
=8,2/7,1=1,155.
Диалоговое окно функции FРАСПОБР представлено на рис. 1. Степени свободы

 =28+12=40.
=28+12=40.
Критические значения  - критерия при различных значениях уровня значимости приведены в таблице 1.
- критерия при различных значениях уровня значимости приведены в таблице 1.

Рис.1. Диалоговое окно функции FРАСПОБР
Т а б л и ц а 1
Результаты расчета в среде ЭТ

Так как расчетное значение  - критерия меньше критических значений при всех уровнях значимости, то гипотеза о равенстве дисперсий подтверждается.
- критерия меньше критических значений при всех уровнях значимости, то гипотеза о равенстве дисперсий подтверждается.
Определим общую дисперсию
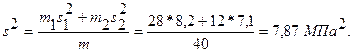
Вычислим расчетное значение 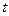 - статистики
- статистики
 .
.
Критические значения 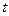 - статистики, полученные с помощью статистической функции СТЬЮДРАСПОБР при различных значениях уровня значимости, приведены в таблице 1.
- статистики, полученные с помощью статистической функции СТЬЮДРАСПОБР при различных значениях уровня значимости, приведены в таблице 1.
Диалоговое окно этой функции представлено на рис. 2.

Рис. 2. Диалоговое окно функции СТЬЮДРАСПОБР
Расчетное значение 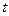 - статистики при всех уровнях значимости меньше критического значения. Следовательно, между средними значениями прочности бетона двух выборок нет существенного различия.
- статистики при всех уровнях значимости меньше критического значения. Следовательно, между средними значениями прочности бетона двух выборок нет существенного различия.