 |
|
Математична постановка
Система „імплантат – кісткова тканина – протезна конструкція” моделюється, як кусково-однорідне ізотропне тіло. Будемо вважати, що напружено-деформований стан пружного тіла (системи „імплантат – кісткова тканина – протезна конструкція”) описується співвідношеннями лінійної теорії пружності.
Розглядаємо в декартовій системі координат 
просторове тіло, яке займає обмежену область 
з неперервною за Ліпшицем границею 
. 
– кусково-однорідне ізотропне тіло, тобто 
, де 
– кількість імплантатів (рис 1.2).
Рис 1.2. Схематичне зображення конструкції
– імплантати, 
– губчаста кісткова тканина, 
– кортикальна кісткова тканина, 
– протезна конструкція.
Матеріали областей 
є ізотропними і відрізняються своїми фізико-механічними властивостями: модулем Юнга 
та коефіцієнтом Пуасона 
.
В математичній моделі, що описує поставлену задачу, не враховується дія об’ємних (масових) сил.
Напружено-деформований стан тіла визначається з рівнянь рівноваги
, 
, (1.1)
де 
;
Вектор 
визначає напруження тіла ;
Оскільки, тензор деформації
(1.2)
може бути представлений як вектор, враховуючи те, що він є симетричним, і відповідно має лише шість різних між собою складових.
-компоненти напруження в площині, перпендикулярній осі 
, 
- в площині, перпендикулярній осі 
, 
- в площині, перпендикулярній осі 
. Перший індекс в цих позначеннях характеризує орієнтацію площини, а другий – напрямок дії відповідної складової напруження. Нормальні напруження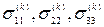 
вважаються додатними, якщо вони напрямлені по зовнішній нормалі до площини. Додатні напрямки дотичних напружень на границі приймаються як ті, що співпадають з додатними напрямками відповідної осі. Якщо ж зовнішня нормаль напрямлена протилежно до відповідної осі, то і додатні дотичні напруження в цій границі діють у від’ємних напрямках до двох інших осей. Як відомо, має місце наступна властивість парності дотикаючих напружень
(1.3)
Крім того, на частині 
зовнішньої поверхні вектор переміщень 
задовольняє кінематичні (головні) крайові умови,тобто на частині задані переміщення. Оскільки наша конструкція закріплена на частині , то вектор переміщень рівний нулю
, 
, , ( 
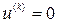), (1.4′)
на частині 
– статичні (природні) крайові умови, тобто заданий зв’язок між поверхневими силами та напруженнями біля поверхні тіла
, 
, , ( 
), (1.4″)
де 
– вектор заданих поверхневих зусиль;
- компоненти одиничного вектора нормалі 
до поверхні тіла, 
;
, 
.
Вважаємо, що контакт між областями ідеальний. Це означає, що на поверхні спряження областей 
та 
виконуються умови ідеального механічного контакту
, (1.5′)
, (1.5″)
де 
, 
– компоненти вектора поверхневих зусиль, що діють на частині поверхні контакту 
областей та .
В областях мають місце геометричні співвідношення Коші, що встановлюють зв’язок між компонентами деформації і компонентами переміщення. Якщо деформація і переміщення малі, то між ними існує лінійна залежність, що виражається рівняннями
, 
, (1.6)
де вектор 
визначає деформації тіла .
Оскільки, тензор деформації
(1.7)
може бути представлений як вектор.
- відносні зміни довжин нескінчено малих відрізків, першопочатково (до деформації) паралельних осям 
, , відповідно; вони вважаються додатними, якщо відбуваються видовження відрізків, і від’ємними – у випадку їх скорочення. 
- суть деформації зсуву, які являють собою зміни кутів між елементарними відрізками, первинно паралельними тим координатним осям, які вказані в нижніх індексах. Деформації зсуву вважаються додатними, якщо кути між відрізками, орієнтованими в додатних напрямках координатних осей, стають гострими.
В матричній формі співвідношення Коші мають вигляд:
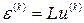, (1.8)
де 
– матриця диференціальних операторів
(1.9)
Складові вектора деформації не є взаємонезалежними, а повинні задовольняти умові компабільності Сен-Венана.
Якщо з умови (1.8) виключити переміщення 
, то між компонентами деформації отримуємо шість диференціальних співвідношень, що називаються умовами сумісності (чи нерозривності) деформації Сен-Венана:
(1.10)
Вважаємо також, що в областях виконуються фізичні співвідношення узагальненого закону Гука, що встановлюють зв’язок між напруженнями і деформаціями.Згідно цього закону компоненти деформації є лінійними функціями компонент напруження. Для ізотропного тіла закон Гука в матричній формі має вигляд:
(1.11)
де 
- матриця пружних констант закону Гука, яка у випадках ізотропного однорідного матеріалу може бути представлена з допомогою коефіцієнтів Ламе 
і 
:
(1.12)
або відповідно коефіцієнтів Юнга - і Пуассона -
(1.13)
при відомих зв’язках між цими елементами:
, 
; (1.14)
та відповідно:
, 
(1.15)
Матрична рівність закону Гука може бути представлена співвідношеннями :
;
; (1.16)
;
; 
; 
.
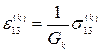де 
- модуль зсуву,
. (1.17)
Розв’язавши рівняння (1.16) відносно напружень, можна представити закон Гука у формі Ляме
, 
,
, 
, (1.18)
, 
,
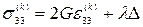де 
, 
.
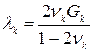Рівняння (1.1), (1.4), (1.5), (1.6), (1.11) повністю визначають крайову задачу статичної взаємодії однорідного кусково-ізотропного тіла за умов ідеального контакту.
Розв’язок цієї системи можна шукати або в переміщеннях, або в напруженнях, розглядаючи відповідну систему диференціальних рівнянь. Цим двом підходам відповідають і різні варіаційні принципи (принцип мінімуму потенціальної енергії Лагранжа та принцип мінімуму додаткової роботи Кастильяно відповідно). Можна також шукати розв’язок змішаної системи (відповідно існують мішані варіаційні принципи, а також гібридні та узагальнені варіаційні методи)
Для розв’язку задач теорії пружності в переміщеннях необхідно рівняння рівноваги для точок тіла ( ) представити в переміщеннях.З цією метою виражаємо напруження через деформації в формі Ляме (1.18), а деформації представимо через переміщення за співвідношеннями Коші (1.16).
Отримуємо
(1.19)
Це – рівняння Нав’є, лінійні диференціальні рівняння відносно компонент векторів переміщень . З допомогою пружних сталих Ляме вони приймають вигляд
(1.20)
і в такій формі називаються рівняннями Ляме.
До цих рівнянь необхідно долучити граничні умови. Якщо на поверхні тіла задані переміщення, то граничні умови зводяться до вимоги, щоб в точках поверхні шукані функції 
прийняли задані значення. Однак в нашому випадку геометричні умови задаються лише на частині поверхні , а на частині задаються поверхневі навантаження і задовольняються статичні граничні умови (1.14″). Їх потрібно також записати через переміщення, в результаті чого вони приймуть вигляд:
де 
.