 |
|
ПОНЯТИЕ ЧИСЛОВОГО РЯДА И ЕГО СУММЫ
УДК 517.5
ББК 22.19
Составители: С.В. Бушков, Л.В. Коломиец
Рецензент: д-р техн. наук, проф. Б.А. Горлач
Приложения и приближенное вычисление определенных интегралов:метод. указания / сост. С.В. Бушков, Л.В. Коломиец. -Самара: Изд-во Самар. гос. аэрокосм. ун-та, 2009. –48 с.
Методические указания составлены в соответствии с действующей программой по курсу высшей математики для инженерно-технических специальностей Самарского государственного аэрокосмического университета. Указания обеспечивают полную теоретическую и методическую поддержку практических занятий по темам «Приложения определенного интеграла» и «Приближенное вычисление определенных интегралов».
Методические указания могут быть рекомендованы студентам для самостоятельной работы и подготовки к экзаменам.
© Самарский государственный
аэрокосмический университет, 2009
СОДЕРЖАНИЕ
1. Площадь плоской фигуры в декартовых координатах…………………………
2. Площадь плоской фигуры при параметрическом
задании границ…………………………………………………………………..8
3. Площадь плоской фигуры в полярных координатах………..………….....11
ПОНЯТИЕ ЧИСЛОВОГО РЯДА И ЕГО СУММЫ
Рассмотрим числовую последовательность 
Составим из неё новую последовательность по правилу:
,
,
,
. . . . . . . . . . . .
,
. . . . . . . . . . .
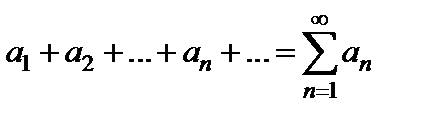называется числовым рядом, числа 
называются членами ряда, 
– общим членом, 
− n-ой частичной суммой ряда.
Определение 1. Числовой ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм при 
, т.е.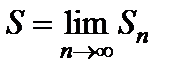 
. Число 
называется суммой числового ряда, в этом случае записывают: 
. Если 
или не существует, то ряд 
называется расходящимся.
Пример 1. Рассмотрим геометрическую прогрессию
Из школьного курса математики известно, что сумма её первых членов равна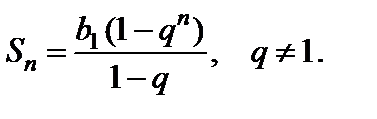 
Возможны следующие случаи:
1) Если 
, то 
, следовательно, 
, т.е. ряд расходится.
2) Если 
, то 
следовательно,
, т.е. ряд 
сходится.
3) Если 
, то 
, т.е. сумма нечетного числа членов ряда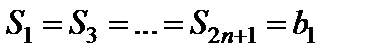 
, а сумма четного числа членов 
. Получили последовательность частичных сумм 
которая не имеет предела. Следовательно, при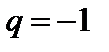 
ряд 
расходится.
Таким образом, ряд 
, составленный из членов геометрической прогрессии, сходится при 
и расходится при 
.
Пример 2. Найдите сумму ряда 
.
Решение. Разложим общий член ряда 
на простейшие дроби:
.
Найдём n-ую частичную сумму ряда:
Заметим, что второе слагаемое скобки с номером «к» взаимно уничтожается с первым слагаемым скобки с номером «к+1», поэтому в итоге частичная сумма ряда имеет вид: 
.
Найдем предел:
Ответ: сумма данного ряда равна 