 |
|
Разложение функций в степенные ряды.
Функция  разлагается в степенной ряд
разлагается в степенной ряд  или в ряд
или в ряд  , если:
, если:
1) этот степенной ряд сходится; 2) его сумма на интервале сходимости равна  .
.
Известно, что функцию  можно разложить в ряд Тейлора. Однако, чисто формальное разложение в ряд Тейлора может привести к неверному результату, т.к.
можно разложить в ряд Тейлора. Однако, чисто формальное разложение в ряд Тейлора может привести к неверному результату, т.к.
1) ряд может сходиться к  только в некоторой области; 2) ряд может сходиться, но не к
только в некоторой области; 2) ряд может сходиться, но не к  ; 3) ряд может расходиться.
; 3) ряд может расходиться.
Рассмотрим условия разложения функции в ряд Тейлора.
Теорема 7.1. Для того чтобы ряд Тейлора сходился к функции  необходимо и достаточно, чтобы остаточный член ряда стремился к 0 при
необходимо и достаточно, чтобы остаточный член ряда стремился к 0 при  .
.
Теорема 7.2. Если производные любого порядка функции  ограничены одной и той же постоянной, т.е.
ограничены одной и той же постоянной, т.е.  ,
,  ,
,  , то ряд Тейлора сходится в
, то ряд Тейлора сходится в  к
к  .
.
Теорема 7.3. Разложение функции в ряд Тейлора единственно.
Приведем разложение основных элементарных функций в степенные ряды.
1)  ,
, 
2)  ,
, 
3)  ,
, 
4)  ,
, 
5)  ,
, 
6)  ,
, 
7)  ,
, 
8)  ,
, 
9)  ,
, 
Пример 23. Разложите функцию  в ряд Тейлора по степеням
в ряд Тейлора по степеням  .
.
Решение. Так как  , то
, то  . Так как разложение для
. Так как разложение для  действительно при
действительно при  , то и функция
, то и функция  разлагается в ряд Тейлора при
разлагается в ряд Тейлора при  .
.
Пример 24. Разложите функцию  в ряд Тейлора по степеням
в ряд Тейлора по степеням  .
.
Решение. Представим дробь  в виде суммы простейших дробей:
в виде суммы простейших дробей:

и разложим каждую простейшую дробь в правой части равенства по формуле для суммы бесконечно убывающей геометрической прогрессии:
 , где
, где  .
.
 .
.
Это разложение имеет место лишь для  , удовлетворяющих неравенству
, удовлетворяющих неравенству  или
или  .
.
Так как  для
для  ,
, 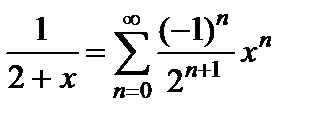 для
для 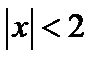 , то разложение функции
, то разложение функции 
 верно при
верно при  (как пересечение областей сходимости).
(как пересечение областей сходимости).
Пример 25. Разложите функцию  в ряд Тейлора по степеням
в ряд Тейлора по степеням  .
.
Решение. Разложим аргумент логарифма на множители:  . Тогда
. Тогда  . И, применяя формулу
. И, применяя формулу 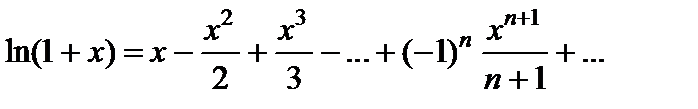 , где
, где  , запишем:
, запишем:
 ,
,
это представление верно при  или
или  .
.
 ,
,
это равенство имеет место при 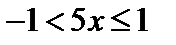 или
или  .
.
Объединяя полученные результаты, получаем разложение данной функции в ряд Тейлора по степеням  :
:
 ,
,
причём это разложение справедливо при 