 |
|
Приложения степенных рядов.
Рассмотрим следующие приложения степенных рядов:
1) Приближенное вычисление значений функции. Функцию разлагают в степенной ряд, оставляют первые n членов. Погрешность равна остатку ряда 
. Для оценки погрешности применяют приёмы:
а) если ряд 
знакоположительный, его сравнивают с геометрической прогрессией;
б) если ряд 
знакочередующийся, применяют признак Лейбница, т.е. используют свойство 
.
Пример 26. Оценить погрешность приближённого равенства
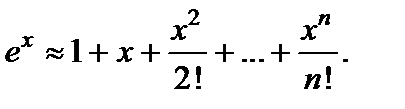
Решение.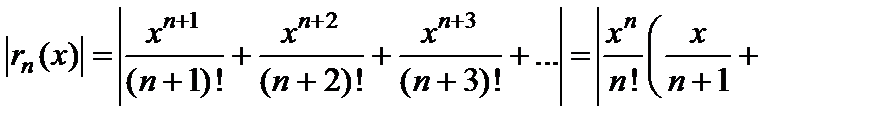 
Если 
, то, применяя к выражению в скобках формулу для суммы бесконечно убывающей геометрической прогрессии, получаем
.
Таким образом,
.
Пример 27. Вычислить 
точностью до 10-4.
Решение. Так как 
, то, применяя формулу 
при 
, запишем 
В правой части этого равенства числовой знакочередующийся ряд. По признаку Лейбница сумма такого ряда не превосходит первого отброшенного члена. Заметим, что 
, поэтому для вычисления суммы знакочередующегося ряда достаточно взять первые два слагаемых и считать, что 
.
2) Приближенное вычисление пределов.
Пример 28.Вычислите приближенно предел 
.
Решение. При 
получаем неопределенность вида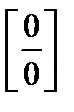 
. Но применять таблицу эквивалентных бесконечно малых нельзя, так как в числителе разность бесконечно малых одного порядка. Вычислим этот предел, разложив слагаемые в числителе в степенные ряды.
это разложение верно для любых действительных 
.
это разложение имеет место при 
, но 
, поэтому в нашем случае можно применить указанное представление.
С учётом вышесказанного запишем:
.
3) Приближенное вычисление интегралов.
Пример 29.Вычислите интеграл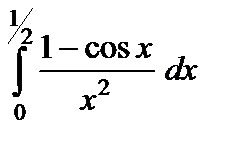 
точностью до 
.
Решение. Разложим 
в ряд Тейлора по степеням 
:
Тогда
Подставим полученное разложение подынтегральной функции в исходный интеграл:
.
Под знаком интеграла степенной ряд 
. Применяя обобщенный признак Даламбера, можно доказать, что этот ряд сходится при любом действительном 
.
Следовательно, он сходится равномерно на отрезке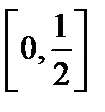 
. Поэтому его можно почленно интегрировать на этом отрезке. Проинтегрируем:
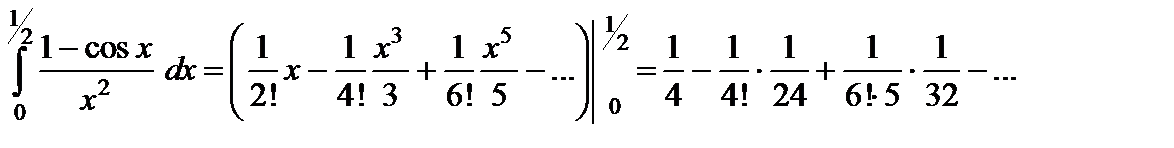
В правой части равенства 
числовой знакочередующейся ряд, его сумма по признаку Лейбница не превосходит первого отброшенного члена. Так как 
, то для вычисления интеграла с указанной точностью достаточно взять первые два слагаемых, т.е.
.