Главная | Обратная связь

Келісілген нормалар.

Информатика

Информатика

мамандықтары үшін

 

 

 

 

Ќарағанды

 

 

Құрастырғанр ф.-м.ғ.к., доцент Бабалиев Ә.М.

оқытушы Муратхан Р.

 

Оқу-әдістемелік кешен «Сандық әдістер» пәні бойынша жалпы мағлұматтар алуға арналған. Бұл пән алгебраның, математикалық талдаудың, жәй дифференциалдық теңдеуледің есептерін компьютерде шешу жолдарымен таныстырыады.

"Сандық әдістер"/ Құрас.: Бабалиев Әмірбек Мауленбекович, Муратхан Райхан. Қарағанды, ҚарМУ баспасы, 2006, 171 бет.

 

Ó Қарағанды мемлекеттік университеті, 2006
1. ПӘННІҢ ОҚУ БАҒДАРЛАМАСЫ – SYLLABUS

 

1.1. Оқытушылар туралы мәліметтер:

Бабалиев Әмірбек Мауленбекұлы, физика-математика ғылымдарының кандидаты, доцент, қолданбалы математика саласының маманы.

Муратхан Райхан есептеу математика саласының маманы.

Оқытушылармен байланыс: сабақ кестесі бойынша «Қолданбалы математика және информатика» кафедрасында.

 

1.2 Пән туралы мағлұматтар:

Сандық әдістер, 3 кредит, математика факультеті.

Оқу жоспарынан үзінді

Міндетті копонент

Курс	Семестр	Кредит	Лекция	Практ.сабақ	ОСӨЖ	СӨЖ	Барлығы	Бақылау формасы
								Емтихан

 

1.3 Пререквизиттер:Бұл пәнді игеру үшін келесі пәндер бойынша білімі болу керек: алгебра, аналитикалық геометрия, математикалық талдау, дифференциалдық теңдеулер.

 

1.4 Постреквизиттер: Бұл пән бойынша алынған білім келесі пәндерді оқу барысында қажет болады: программалау тілдері, математикалық физиканың сандық әдістері, арнайы курстар.

 

1.5 Пәннің қысқаша мазмұны:

Қателер теориясымен, функцияны жуықтау, сызықты, сызықты емес теңдеулерді, тендеулер жүйелерін және дифференциалды теңдеулерді жуықтап шешу әдістерімен таныстыру.

 

Пәнді игерудегі міндеттер:

Пәнді оқығаннан кейін студент

қолданбалы математиканыњ есептерін шешудің алгоритмін жасай білуі және оны сандық әдістердің көмегімен шеше білуі керек.

 

1.6 Пән бойынша берілген тапсырмаларды орындау және тапсыру графигі

 

№	Жұмыс түрлері	Тапсырманың мақса-ты мен мазмұны	Пайдаланатын әдебиеттер	Орындау ұзақтылығы	Баллдары (рейтинг-шкаласына сәйкес)	Бақылау формасы	Тапсыру уақыты (семестрдің аптасы)
	Бақылау жұмысы	аралық бақылау, 2.6 пункті	п. 1.7	1 сағат		жазбаша
	Курстық жұмыс	ағымдық. Бақылау, 2.6 пункті	п. 1.7	10 апта		қорғау
	Курстық жоба	аралық бақылау, 2.6 пункті	п. 1.7	13 апта		қорғау
	Экзамен	Ақырғы бақылау, 2.7, 2.8 п.	п. 1.7	3 сағат		Ауызша, тест

1.7 Әдебиеттер тізімі

Негізгі

1. Демидович Б.П., Марон И.А. Основы вычислительной математики. М. Наука. 1966 г.

2. Сұлтангазин Ө., Атанбаев С., Есептеу әдістерінің қысқаша теориясы ,Т.1, Алматы, 1995 ж.

3. Сұлтангазин Ө., Атанбаев С., Есептеу әдістерінің қысқаша теориясы ,Т..2, Алматы, 2001 ж.

4. Марчук Г.И., Методы вычислительной математики. М. 1989 г.

5. Березин И.С.,Жидков Н.П. Методы вычислений т.1,2, М. Наука,1966 г.

6. Бахвалов Н.С. и др. Численные методы. М. Наука. 1987 г.

7. Самарский А.А., Гулин А.В. Численные методы. М. Наука. 1989 г.

Қосымша

8. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике. М. Высшая школа. 1990 г.

9. Калиткин Н.Н. Численные методы. М. Наука. 1987 г.

10. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М. Наука. 1990 г.

11. Н.А. Альмуханбетов, А.М. Бабалиев. Линейная алгебра и элементы вычислительной математики, Караганда, 1988.

12. Н.А. Альмуханбетов, А.М. Бабалиев. Численные методы линейной алгебры и дифференциальных уравнений, Караганда, 1988.

13. Д.К.Фаддеев, В.Н.Фаддеева. Вычислительные методы линейной алгебры, Санкт-Петербург, 2002.

14. В.И. Киреев, А.В. Пантелеев. Численные методы в примерах и задачах, Москва, «Высшая школа», 2004.

 

1.8 Баға туралы мәліметтерде білімді бағалау шкаласы, білімді бағалау критериі және тапсырманы орындауда қойылатын талаптар беріледі.

 

Рейтинг-шкаласы

Бақылау формасы	Баллдары
Ағымдық бақылау
Аралық бақылау
Үй жұмысы
Қорытынды бақылау
Барлығы:

 

 

1.9 Курстың процедурасы мен саясаты

Студенттердің міңдеттері:

­ оқу процессіне белсенді қатысу, академиялық сабақтарға қатысу, лекциялық және практикалық сабақтар жазбасын таза жазу;

­ лекциялық және практикалық сабақтарда, қосымша оқулықтардан өзіндік жұмыс бойынша алынған білім мен дағдыны дер кезінде бекітіп және дамытып отыруы ;

­ оқу графигінің барлық талаптарын уақытында орындап отыруы ;

Оқу графигін бұзса, емтиханда болмаса – жазғы семестрде қайтадан оқуы керек.

 

2. ПӘН БОЙЫНША ОҚУ-ӘДІСТЕМЕЛІК МАТЕРИАЛДАР

2.1 Курстың тақырыптық жоспары

2.1.1. Дәріс сабақтары, олардың атаулары және сағат бойынша көлемі

 

№	Тақырыбы.	Сағат	Әдебиет
	Теңдеулер жүйесін итерация әдістерімен шешу. 1. Матрицамен вектордың нормалары. 2. Сызықтық алгебрадағы шектердің түсінігі. 3. Итерация процессінің принципі және бертіндеп жуықтау әдісі. 4. Минималь ауытқу әдісі. 5. Жылдам түсү әдісі.		[1.3.5.7.9]
	Жєй дифференциалдыќ теңдеулерге ќойылѓан Коши есебін шешу 1. Тор. Торлыќ функциялар туралы т‰сінік 2. Есептің қойылуы және оны шешудің мысалдары. Эйлердіњ єдістері 3 Рунге-Кутта әдісі. 4. Көп қамды Адамс әдістері.		[2.4.6.9]
	Айрымдыќ схемалар туралы т‰сінік. 1. Жєй дифференциалдыќ операторларды жуыќтау 2. Шекаралыќ есептерді жуыќтау 3. Айырымдыќ есептіњ шешуініњ жинаќталуы туралы т‰сінік. 4. Айырымдыќ есептіњ орныќтылыѓы туралы т‰сінік.		[2,6,7,10]
	5. Айырымдыќ есептіњ шешуініњ жинаќталуы туралы теорема 6. Айрымдыќ схеманыњ орныќтылыѓын зерттеу жолдары. 7. Сызыќтыќ операторлар жєне олардыњ негізгі ќасиеттері. 8. Екінші ретті жєй дифференциялдыќ шекаралыќ есептерді жуыќтау		[2,6,7,10]
	Жиынтығы

2.2. Дәріс сабақтарының тезисі

1-тақырып

Сызықтық теңдеулер жүйесін шешу әдістері

Теңдеулер жүйелерін шешу жолдары әдетте, дәл және итерациялық әдістер болып екі топқа бөлінеді.

Дәл әдістер орындалатын арифметикалық амалдар саны санаулы болатын өрнектерден тұрады. Теңдеулер жүйесін шешу үшін қолданылатын Крамер, Гаусс, қуалау әдістері осы топқа жатады. Жүйені анықтайтын деректер дәл берілгенде және есептеулер дәл орындалғанда, олар жүйенің дәл шешімін беруі тиіс.

Итерациялық әдістер бір немесе бірнеше параметрлері үнемі өзгеріп тұратын алгебралық біртекті өрнектерден құралады. Олар жүйенің жуық шешімін векторлар тізбегінің шегі ретінде анықтайды. Тізбектелген алгебралық өрнектерді итерациялық әдістің есептеу алгоритмі деп атайды.

Итерациялық әдісті қолданғанда ескеретін мәселе, оның тек жинақтылығығана емес жинақталу жылдамдығы да қарастырылуы керек. Себебі әр итерациялық әдіс, теңдеулер жүйесінің матрицасының түріне қарай, тез немесе өте жәй жинақталуы мүмкін, ал кейбір жағдайда жинақталмауы да мүмкін. Сондықтан итерациялық әдісті қолданудан бұрын теңдеулер жүйесін, итерациялық әдіс жинақталатындай, эквивалентті теңдеулер жүйесімен алмастырады.

Енді жоғарыда аталған мәселелерге жеке-жеке тоқталайық.

 

§1. Векторлар мен матрицалардың нормалары және олардың негізгі қасиеттері.

 

1.1.Векторлардың нормалары.R_n векторлық кеңістікте векторы берілсін. Мұндағы х_і-вектордың і-координаты.

Анықтама. Х векторының нормасы-||X|| деп мна шарттарды қанағаттандыратын теріс емес санды айтамыз:

1) ||X|| >0, егер болса және ||X||=0, егер Х=0 болса;

2) ||cX||=|c| ||X|| , с-кез-келген сан;

3) ||X+У||≤ ||X||+||У|| (үшбұрыш теңсіздігі) .

Соңғы екі шарттан мына теңсіздікті алуға болады

||X-У|| ≥ ||X||-||У||.

Шынында да ||X|| =||X+У-У||≤ ||X-У||+||У||.

Осыдан ||X|| - ||У||≤ ||X-У||.

Сызықтық алгебрада вектордың төмендегі үш нормасы жиі қолданылады:

1) (кубтық норма); (1.1)

2) (октаэдрлік норма); (1.2)

3) (сфералық норма); (1.3)

Соңѓы норманы вектордың ұзындығы дейді. Бұл үш нормада анықтаманың үш шартын да қанағаттандырады. Бірінші және екінші шарттардың орындалуы айқын болғандықтан, бұлар үшінші шартты да қанағаттандыратынын көрсетейік.

Бірінші және екінші нормалар үшін мына теңсіздіктер орындалады:

;

;

Ал үшінші норма үшін Коши-Буняковский теңсіздігін пайдалансақ:

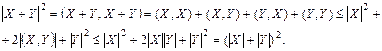Осыдан

.

Егер , 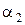оң нақты сандары үшін векторлардың нормалары 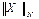, мына шартты қанғаттандырса , онда оларды эквивалентті нормалар дейді. Жоғарыда көрсетілген нормалар өзара эквивалентті. өйткені олар мына теңсіздіктерді қанағаттандырады.

 

(1.4)

(1.5)

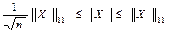(1.6)

(1.4),(1.5) теңсіздіктері мен (1.6) теңсіздігінің оң жағы айқын болғандықтан, біз (1.6) теңсіздігінің сол жағын дәлелдесек болғаны. Шынында да

.

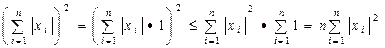Осыдан .

Х^(к)-векторлар тізбегінің Х векторына жинақталуы үшін шартының орындалуы қажетті және жеткілікті. Бұл шарт кубтық норма үшін айқын, ал қалған екі норма үшін бұл шарттың орындалуы (1.4),(1.5) теңсіздіктерінен шығады. Сондықтан итерациялық әдістердің жинақталуын зерттегенде, векторлардың кез-келген, жоғарыда көрсетілген нормаларын пайдалануға болады.

 

1.2.Матрицалардың нормалары.

Анықтама. Берілген А квадрат матрицаның нормасы- деп теріс емес және келесі төрт шартты қанағаттандыратын санды айтамыз:

1) , егер және =0, егер А=0;

2) ;

3) ;

4) .

Матрицаның нормасын әртүрлі жолдармен алуға болады. Мысалы көп қолданылатын нормаларға мына нормаларды жатқызуға болады:

,

.

Бұл нормалар бірінші үш шартты қанағаттандыратыны айқын болғандықтан 4-ші шарттың орындалуын дәлелдейік:

Айталық, А=(а_іj ), B=(b_іj ) болсын. Онда .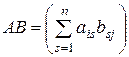

Сондықтан

Дәл сол сияқты

.

Коши-Буняковский теңсіздігі бойынша

.

Осыдан

.

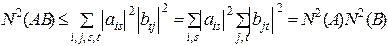Яғни

.

 

Келісілген нормалар.

Көптеген есептерде матрица мен вектордың нормалры қатар қолданылатындықтан, олар бір-бірімен келісілген болуы тиіс.

Анықтама. Егер А матрицасы мен Х векторы үшін шарты орындалса, онда А матрицасы мен Х векторының нормалары келісілген дейміз.

Матрицаның М(А) нормасы вектордың кубтық, октаэдрлік, сфералық нормаларымен келісілген, ал N(A) тек сфералық нормамен келісілген.

Шынында да, егер Х=(x₁,x₂,…,x_n)' болса , онда

,

Ақырында

теңсіздігінен М(А) мен N(A) нормаларының вектордың сфералық нормасымен келісілгенін көреміз.

Енді Х векторының нормасымен келісілген А матрицасының, шамасы жағынан ең кіші, нормасын табуды қарастырайық.

А матрицасының нормасы ретінде ||X||=1 болған жағдайдағы АХ векторының ең үлкен нормасын алсақ, яғни

(1.7)

болса, онда бұл шама норманың анықтамасының барлық төрт шартын қанағаттандырумен қатар келісілгендіктің де шартын қанағаттандырады:

 

1-шарт. Айталық, . Онда ||X||=1 вектор табылып, болады. Сондықтан болғандықтан >0. Егер А=0 болса, онда .

 

2-шарт. Екінші шарттың орындалуы мына теңдіктерден шығады:

.

Келісілгендік шарт.

Егер кез-келген вектор болса, онда векторының нормасы ||Х||=1. Сондықтан .

 

3-шарт. А+В матрицасы үшін ||A+B||=||(A+B)X₀|| теңдігі орындалатындай нормасы бірге тең (|(X₀||=1) Х₀ векторын табамыз. Сонда

 

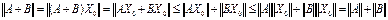
4-шарт. АВ матрицасы үшін ||X₀||=1 және ||ABХ₀||=||AB|| теңдігін қанағаттандыратын Х₀ векторын табамыз. Сонда

.

Сонымен біз (1.7) нормасы норманың анықтамасының барлық шарттарын және келісілгендік шартын қанағаттандыратындығын көрдік. А матрицасының (1.7) түріндегі нормасын берілген вектордың нормасына бағынған норма дейміз.

Енді бағынған норманың мәні басқа келісілген нормалардың мәнінен үлкен еместігін көрсетейік. Шынында да, L(A)- матрицаның вектордың нормасымен келісілген нормасы, ал -вектордың нормасына бағынған нормасы болсын.

Онда нормасы бірге тең Х₀ векторы табылып ||A||=||AХ₀|| теңдігі орындалады. Ал екенін ескерсек, онда екенін көреміз.

Енді жоғарыда көрсетілген вектордың нормаларына бағынған матрицаның нормасын қарастырайық:

 

1. .

Бұл нормаға бағынған матрицаның нормасы

. (1.8)

Шынында да, ||Х||₁ =1 болсын.

Онда

,

яғни

.

Енді шынында да өрнегіне тең екенің дәлелдейік.

Ол үшін ||X₀||=1 және болатын Х₀ векторын тұрғызайық.

Айталық, өзінің ең үлкен мәнін і=j болғанда қабылдасын. Ал Х₀ векторының координатасын

деп алсақ, онда ||X₀||=1. Сонымен қоса және

,

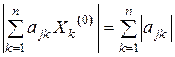болғандықтан

.

Осыдан .

Сонымен

.

2.

Бұл нормаға бағынған матрицаның нормасы-

. (1.9)

Шынында да болса, онда

Енді Х₀ векторын былайша алайық:

өрнегі өзінің ең үлкен мәнін k=j болғанда алатын, ал k¹j болғанда Х_k⁽⁰⁾ =0және Х_j⁽⁰⁾ =1 болсын.

Онда

.

Сонымен

.

3. .

Бұл нормаға бағынған матрицаның нормасы-

мұндаλ-А^*А матрицасының ең үлкен меншікті саны. Шынында да,

Бірақ |AX|²=|АХ,АХ|=|Х,А^*АХ|, ал А^*А-эрмиттік (симметриялы оң анықталған) матрица. Айталық, λ₁ ең үлкен меншікті сан болсын, онда |X|=1 болғандамах(Х,А^*АХ)= λ₁.

Сондықтан (1.10) формуласы арқылы табылған матрицаның нормасын - спектрлік норма дейді. Осы формуланы пайдаланып А^-1 кері матрицасының спектрлік нормасын анықтауға болады: ,

мұнда λ_k(А'A) - A'A матрицасының меншікті сандары.

 

§2. Матрицалар мен векторлар тізбегінің жинақталуы.

 

Сызықтық алгебрадағы шектер туралы түсініктер көбіне итерациялық әдістерді қарастырған кезде пайдаланылады. Сондықтан біз матрица мен векторлар тізбектерінің жинақталуы туралы ұғымды және матрица мен векторлар тізбегінің жинақталу шаттарын қарастырамыз.

2.1.Матрицалар мен векторлар тізбегінің шегі туралы түсінік.

Айталық, берілген векторлар тізбегінің координаталары

х₁⁽¹⁾,…, х_n⁽¹⁾,…; … ; х₁^(k),… х_n^(k) болсын.

Егер {X^(к)} тізбегі Х=(x₁, x₂, … ,x_n) векторына жинақталатын болса, онда оны былайша жазады:

, немесе Х^(к) 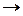Х.

Бұл жағдай (і=1,…,n) болғанда орындалады.

Егер ќатарыныњ шегі бар болса, онда 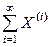жинақталатын қатар дейміз.

Енді А⁽¹⁾, А⁽²⁾, … , А^(к), … матрицалар тізбегі берілсін және әрбір А^(к)={a_іj^(k)} болсын. Егер барлық і,j үшін шарты орындалса, онда {А^(k)} тізбегі А={a_іj} матрицасына жинақталады дейміз және оны былай жазады:

, немесе A^(к) 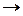A .

Егер квадрат матрицалар тізбегі {А^(k)} ерекше емес А матрицасына жинақталатын болса, онда жеткілікті үлкен к үшін А^(k) матрицасының кері матрицасы бар болады және .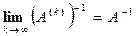

Шынында да, егер A^(к) 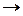A болса, онда A^(к) матрицасына сыбайлас матрица - В^(к), А матрицасына сыбайлас В матрицасына жинақталады. Себебі В^(к) мен В-ның элементтері тиісінше А^(к) мен А-ның элементтерінен тұратын полином.

Сол себебті және к-ның белгілі бір мәнінен бастап . Осыдан (A^(к))^-1 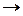A^-1 , себебі .

Теорема. Егер А матрицасы {А^(k)} тізбегінің, ал F-{F^(k)} тізбегінің шегі болса, онда А^(k) Х^(k)= F^(k) жүйесінің шешуі АХ=F жүйесінің шешуіне жинақталады.

Дәлелдеу. Шынында да

.

Теорема дәлелденді.

Егер матрицаның элементтері t параметрі бойынша дифференциалданатын болса, онда .

Егер A(t)={a_іj(t)}₁ⁿ болса, онда A'(t)={a'_іj (t)}₁ⁿ және мына дифференциялдау ережелері орындалады:

Енді жинақталу түсінігіне байланысты бірнеше теоремаларды дәлелдейік.

 

2.2. Жинақтылық теоремалары.

2.1-Теорема. А^m 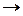0 болуы үшін, А матрицасының барлық меншікті санының модулі бірден кіші болуы қажетті және жеткілікті.

Дәлелдеу. Кез-келген ерекше емес матрица-С үшін, А^m және

(С^-1АС)^m= С^-1А^mC нөлге бірдей жақындайды, немесе бірдей жақындамайды. Сондықтан теореманы Жорданның канондық матрицасы үшін дәлелдесек болады.

Жордан түрлендіруі арқылы А матрицасын мынандай түрге келтірейік:

 

,

мұндағы: , (n_і- Λ_і матрицасыныњ µлшемі).

-ді Жордан жәшігі деп атайды. Ал Λ^m=С ^mC^-1 және

(n₁+n₂+…+n_k=n)

болғандықтан болуы үшін болуы қажетті және жеткілікті.

Сондықтан матрицасының нөлге жинақталу шарттарын қарастырайық. Егер m n_і-1 болған жағдайда

 

мұндағы .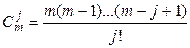

Енді болу үшін <1 шартының орындалуы қажетті, себебі матрицаның диагональ элементтері -ге тең. Сонымен бірге бұл шарт жеткілікті де, өйткені m n_і-1 және кез-келген j=1,2,…,n_і-2 үшін

Теорема дәлелденді.

А^m 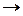0 екенін тексеру үшін А матрицасының меншікті сандары белгілі болуы керек. Бірақ бұл мәселе күрделі болғандықтан, көп жағдайда төменгі жеткіліктілік шарты қолданылады.

2.2-Теорема. болуы үшін А матрицасының ең болмағанда бір нормасы ||A||<1 болуы жеткілікті.

Дәлелдеу. Матрицаның нормасының 4-ші шарты бойынша

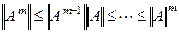. Сондықтан , егер ||A||<1 болса , онда . Ягни . Теорема дәлелденді.

2.3-Теорема.Матрицаның кез-келген нормасының мәнінен меншікті санының модулінің мәні үлкен болмайды.

Дәлелдеу. Матрицаның нормасы-||A||=а болсын. Кез-келген >0 деп алып, матрицасын қарастырайық. <1 болғандықтан 2.2-теорема бойынша . Ал В матрицасының меншікті саны ( -А матрицасының меншікті сандарының мәні) болғандықтан 2.1-теорема бойынша . Осы теңсіздіктегі -ды қалаумызша өте аз шама етіп алуымызға болатындықтан . Теорема дәлелденді.

2.4-Теорема. қатары (Е-А)^-1 матрицасына жинақталуы үшін 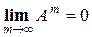болуы қажетті және жеткілікті.

Дәлелдеу. Теореманың қажетті шарты айқын болғандықтан жеткілікті шартын дәлелдейік. Айталық 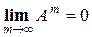болсын, онда 2.1-теорема бойынша А матрицасының меншікті санының модулі 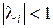болғандықтан . Сондықтан (Е-А)^-1 бар болады. Енді мына тепетеңдікті қарастырайық:

(Е+А+ . . . +А^m)(E-A)=E-A^m+1.

Осы тепетеңдікті оң жағынан (Е-А)^-1-ге көбейтсек

Е+А+…+А^m=(E-A)^-1-A^m+1(E-A)^-1

тепетењдігін аламыз.

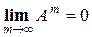болғандықтан m кезде (E+A+…+A^m) 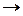(E-A)^-1. Сондықтан =(E-A)^-1. Теорема дәлелденді.

2.5-Теорема. Егер ||A||<1 болса, онда

.

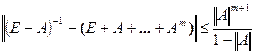Дәлелдеу. (E-A)^-1-(E-A+…+A^m)=A^m+1+A^m+2+… тепе-теңдігінен .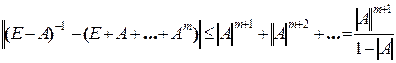

Теорема дәлелденді.

2.6-Теорема.Егер ||A||<1 болса, онда (Е-А)^-1 бар болады және .

Дәлелдеу. 2.4-теорема бойынша (Е-А)^-1 бар болады және теңсіздігі кемімелі прогрессия құрайтындықтан .

Теорема дәлелденді.

 

§3. Матрицаның шарттылығы және теңдеулер жүйесінің орнықтылығы.

Алгебралық теңдеулер жүйесін дәл әдістер арқылы шешкен кездің өзінде де қателер болуы ықтимал. Ондай қателер есептеу кезінде қолданылған дөңгелектеулерде, мәндері өте жақын екі санды бір-бірінен алғанда, тағы сол сияқты кебір арифметикалық амалдарды қолданғанда болуы мүмкін.

Қателер, практикалық есептерді шешу кезінде, теңдеулер жүйесінің матрицасын немесе бос мүшесін (теңдеулер жүйесінің оң жағын) жуықтап алған жағдайда пайда болады. Сондықтан теңдеулер жүйесін шешу кезінде онын матрицасы мен бос мүшесіндегі жіберілген қателер мен арифметикалық амалдарды қолданған кездегі қателер теңдеудің шешуіне қандай әсер тигізетінің қарастырардың алдында мынандай мысалды қарастырайық:

Айталық, матрицасы берілсін.

Егер барлық арифметикалық амалдар дәл орындалған болса, онда матрицаның анықтауышы |A|=1, ал кері матрицасы

.

Енді А матрицасының а₁₁-элементін а₁₁+ деп өзгертсек, онда жаңадан пайда болған

матрицасының кері матрицасы болғанда

болады да, ал болады. Осыдан А мен матрицаларының бір-бірінен айырмашылығы өте аз болса да А^-1 мен ^-1 матрицаларының бір-бірінен айырмашылығы өте үлкен екенін көреміз.

Енді осы жағдайдың қалайша болатындығын, яғни, жалпы айтқанда, берілген матрицаның элементтерін өзгерткен жағдайда кері матрицаның элементтері қалайша өзгеретіндігін қарастырайық.

Айталық, А=(a_іj ), болсын.

АА^-1=E

теңдігін a_іj -элементтері бойынша дифференциялдасақ

.

Осыдан . Бірақ болғандықтан (е_іj- і- жатық жолы мен j- тік жолдарының қиылысуындағы элементі бірге тең, ал қалған элементтері нөлге тең матрица)

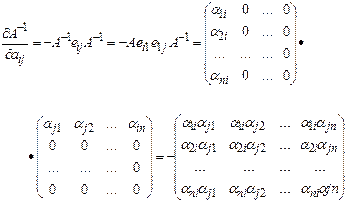
Осыдан ,

.

Сонымен, А матрицасының а_іj элементінің өзгеруіне байланысты кері матрицаның элементтерінің өзгеруі- матрицаның а_іj элементінің өзгеруін кері матрицаның екі элементін көбейтіндісіне көбейткенге тең екенін дәлелдедік. Осыдан кері матрицаның элементтері үлкен сандар болған жағдайда, А матрицасының элементінің аз ғана өзгеруі кері матрицаның элементтерін қатты өзгеріске ұшырататындығын, яғни А^-1 матрицасының орнықсыз екенін көреміз. Кері матрицасы орнықсыз матрицаны шарттылығы нашар(плохо обусловленная) матрица деп атайды. Егер шарттылығы нашар матрицаның элементтері жуықтап алынған болса, онда ол іс жүзінде ерекше матрицаға (|A|=0) айналып кетуі мүмкін. Мысалы |A( )|=1+68 болғандықтан =-1/68 десек, онда |A( )|=0, яғни матрицаның элементтерін анықтау кезінде жіберілген қате 0,02 шамасында болған жағдайда А матрицасы ерекше матрицаға айналуы ықтимал.

Теңдеулер жүйесінің матрицасының шарттылығы нашар болса, онда оның матрицасының элементтері мен бос мүшесінің аз ғана өзгеруі де жүйенің шешімін түпкілікті өзгертіп жібереді. Шынында да

АХ=f теңдеулер жүйесі берілсін.

Х=A^-1f болғандықтан

,

осыдан .

Сол сияқты ,

мұндағы е_і- і-элементі бірге, қалғаны нөлге тең тік бағана.

Осыдан .

Сонымен, егер кері матрицаның элементтері үлкен сандар болса, онда матрицаның элементтері мен бос мүшесінің аз ғана өзгеруі берілген теңдеулер жүйесінің қатты өзгеруіне әкеп соғатынына көз жеткіздік.

Енді теңдеулер жүйесінің орнықтылығын анықтау жолын қарастырайық.

Ах=f (3.1)

жүйесімен қоса

А(х+ )=f+ (3.2)

жүйесі берілсін делік.

Мұнда -жүйенің шешуінің қатесі, -бос мүшенің қатесі.

А = болғандықтан =А^-1 және теңдеулер жүйесінің шешуінің салыстырмалы қателігі- || ||/||x||, бос мүшенің салыстырмалы қателігі - || ||/||f|| десек, онда

.

Осыдан

. (3.3)

(А) санын шарттылық өлшемі деп атайды. Егер (А)>>1 болса, онда А матрицасының шарттылығы нашар, ал бірге жақын сан болса шарттылығы жақсы матрица дейді.

Егер А симметриялы матрица болса, онда , теңдіктерінен

(3.4)

теңдігін аламыз.

Осыдан нөлге жақындаған сайын матрицаның шарттылығы нашарлай түсетінін көреміз.

Сонымен (3.3) және (3.4) формулаларынан мынандай қорытынды шығаруға болады:

Егер (А) саны бірге жақын болса, онда Ах=f орнықтылығы жақсы, ал (А)>>1 болса орнықтылығы нашар жүйе болады.

Ал (А) санының шамасын білу үшін 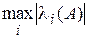, сандарының ара қатынасын анықтау қажет. Бұл мәселе әлі нақты шешімі табылмаған күрделі мәселе болғандықтан А матрицасының меншікті сандарының орналасу облысынан мәлімет беретін мына теореманы қарастырайық.

3.1-Теорема. (Гершгорин теоремасы)

Элементтері кез-келген комплексті сан А=(а_іj) матрицасының меншікті сандары дөңгелектер жиынынан тұратын

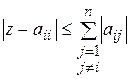(і=1,…,n) (3.5)

облысында жатады.

Дәлелдеу. Айталық -А матрицасының кез-келген менщікті саны, ал Х=(x₁,x₂,…,x_n) менщікті векторы болса, онда (і=1,…,n) немесе .

Х векторының х_і-компоненті модулі бойынша, қалған компоненттерінен үлкен болатындай етіп і индексі алсақ, онда .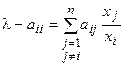

Осыдан .

Сонымен, матрицаның әр меншікті саны _і, центрі а_іі , радиусы дөңгелегінде жататындықтан, онын барлық меншікті сандары осы дөңгелектерді біріктіретін облыста жатады. Теорема дәлелденді.

Теореманың тұжырымына сүйене отырып, ||а_іі||>R_і болған жағдайда А матрицасының меншікті сандары нөлге тең болмайтындығын, ягни оның ерекше емес матрица екенің көреміз.

Практикалық есептерді шешу кезінде берілген теңдеулер жүйесінің матрицасы мен оң жағы көбінесе жуық шамамен берілетіндіктен Ах=f теңдеулер жүйесінің орнына

(А+ А)(х+ )=f+ f (3.6)

жүйесін шешуге тура келеді. Мұнда А, , f -жіберілген қателер. Осы жағдайда жіберілген || ||/||x|| -жүйенің шешуінің салыстырмалы қатесінің қалай өзгеретіндігін мына теоремадан көрүге болады.

3.2-Теорема. Егер А матрицасының кері матрицасы- А^-1 үшін мына шарт орындалса

,

онда (А+ А)^-1 бар болады және

. (3.7)

Дәлелдеу. Алдымен (А+ А)^-1 бар екенің дәлелдейік.

А+ А=A(Е+A^-1 А) және ||A^-1 A||<||A^-1| A||<1 болғандықтан2.4-теорема бойынша (Е+А^-1 А)^-1 бар. Олай болса (А+ А)^-1=(Е+A^-1 А)^-1А^-1.

(3.6) теңдеуінен х+ =(А+ А)^-1(f+ f). Осыдан Ах=f екенің ескере отырып

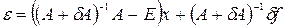(3.8)

теңдігін аламыз. Енді 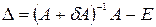матрицасының нормасын бағалайық.

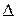=(А+ А)^-1A-E=[A (Е+A^-1 А)]^-1A-E=(E+C)^-1-E,

C= A^-1 А,

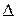=(E+C)^-1(E-(E+C))=-(E+C)^-1C.

(2.6)-теорема бойынша

. (3.9)

Ал (А+ А)^-1=[A (Е+A^-1 А)]^-1=(E+C)^-1А^-1

болғандықтан

. (3.10)

(3.9),(3.10) формулаларын ескере отырып (3.8) формуласының нормасын бағаласақ, онда

.

болғандықтан

.

Осыдан (3.7) формуласын аламыз. Теорема дәлелженді.

Енді мынандай мысалды қарастырайық.

2х₁+х₂=3

2х₁+1,05х₂=3,05

теңдеулер жүйесі берілсін.

Мұнда , |A|=0,1, f=(3; 3,05)^Т.

Егер деп алсақ, онда бұл нормаға бағынған норма ||A||₁=3,05, ||A^-1||=40, және ||f||= 3,05.

Егер бос мүшенің жіберген қатесінің нормасы- || f|| болса, онда теңдеулер жүйесінің шешуінің салыстырмалы қатесі болады.

Ал f=(0; 0,01)^Т болса, онда .

Осыдан теңдеулер жүйесінің шешуін 0,4-ке дейінгі дәлдікпен табуға болатындығын көреміз.

Ал А матрицасы да жуық шамамен берілсе, ягни болса , онда || A||=0,015 болғандықтан .

Сонымен, бұл жағдайда , теңдеулер жүйесінің салыстырмалы қатесі 0,75-ке дейінгі дәлдікпен алынады.

§6. Теңдеулер жүйесін қарапайым итерациялық әдістермен шешу жолдары.

6.1 Итерациялық процесстерді құру принципі.

Көп жағдайда теңдеулер жүйесін дәл әдіске қарағанда итерациялық әдіспен шешкен тиімдірек. Себебі:

1. Егер итерациялық процесс жылдам жинақталатын болса, онда теңдеулер жүйесін шешуге жіберілген арифметикалық амалдар саны мен оны есептеуге жіберілген уақыт үнемделеді.
2. Итерациялық әдіс өзін-өзі түзетін отыратындықта, есептеу кезінде жіберілген қателер жалпы теңдеулер жүйесінің шешуіне әсерін тигізбейді.
3. Итерация әдісінің алгоритмі онша күрделі болмағандықтан ЕЭМ-ға программа оңай құрылады.
4. Теңдеулер жүйесінің матрицасының элементтерінің көпшілігі нөлге тең болған жағдайда итерация әдісінің тиімділігі арта түседі.

Енді осы итерациялық процесті құру схемасымен танысайық.

Айталық ,

(6.1)

теңдеулер жүйесі берілсін және делік. Осы теңдеулер жүйесін шешу үшін

(6.2)

формуласы бойынша , ( -итерацияның -қадамдағы жуықтауы) векторлар тізбегін табамыз.

Х⁰-бастапқы кез-келген вектор, Н¹, Н²,... матрицалар тізбегі .

(6.2)-формуласын итерациялық әдіс дейміз.

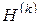
{Н ^(к)} матрицалар тізбегінің түріне қарай (6.2) формуласынан әртүрлі итерациялық процестерді аламыз. Егер ягни -дан тәуелсіз болса, онда итерациялық процесті “стационар” , ал -дан тәуелді болса “стационар емес” деп, ал 12345Следующая ⇒