 |
|
Тейлор формуласы бойынша

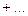
 ,
,
мұнда  .
.
(2.13) теңдігін (2.12) теңдікке қойсақ, онда


 . (2.14)
. (2.14)
(2.14) теңдігінің оң жағы мен сол жағын салыстыру арқылы мына теңдеулер жүйесін аламыз:
 (2.15)
(2.15)
Егер 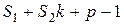 болса, онда (2.15) теңдеулер жүйесінің бір ғана шешуі бар , себебі оның матрицасының анықтауышы - Вандермонд анықтауышы. Егер
болса, онда (2.15) теңдеулер жүйесінің бір ғана шешуі бар , себебі оның матрицасының анықтауышы - Вандермонд анықтауышы. Егер  болса, онда
болса, онда 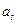 коэффиценттерін әртүрлі жолдармен анықтауға болады.
коэффиценттерін әртүрлі жолдармен анықтауға болады.
Мысалы: Егер  ,
,  ,
,  ,
,  болса,
болса,
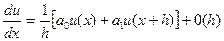 .
.
Енді (2.15) жүйесін қолдансақ, онда

 болады да ,
болады да ,

формуласын аламыз. Ал

деп ұйғарсақ , онда (2.15) жүйеден 
 ,
,  екенін табамыз және
екенін табамыз және

екенін көреміз.
Жалпы бұл әдіс бойынша берілген  операторын қалаған дәлдікпен жуықтауға болады .
операторын қалаған дәлдікпен жуықтауға болады .
Енді жоғарыдағы дифференциалдық операторларды айырымдық функциялармен жуықтауды сипаттау үшін мынадай анықтама енгізейік:
Анықтама 1. Егер берілген  функциялар жиынының
функциялар жиынының  элементі үшін 1.
элементі үшін 1.  жағдайда
жағдайда  , ,онда
, ,онда 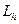 операторы
операторы  операторын жуықтайды (аппроксимациялайды) дейміз.
операторын жуықтайды (аппроксимациялайды) дейміз.
2. 
 (2.16)
(2.16)
теңсіздігі орындалса , онда 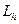 айырымдық операторы
айырымдық операторы  операторын
операторын  функциялар жиынында
функциялар жиынында  -тың
-тың  дәрежесіндегі дәлдікпен жуықтайды (аппроксимация) деп атайды .
дәрежесіндегі дәлдікпен жуықтайды (аппроксимация) деп атайды .
Әдетте  өскен сайын
өскен сайын  функциясына қойылатын талапта өсіп отырады. Мысалы
функциясына қойылатын талапта өсіп отырады. Мысалы  ,
,  айырымдық операторлары үшін
айырымдық операторлары үшін  , ал
, ал  үшін
үшін  талабы қойылады.
талабы қойылады.
4. 
 операторын торлық функциямен алмастыру.
операторын торлық функциямен алмастыру.
 |
Айталық,
 операторы
операторы  облысында анықталсын . Енді осы облысты
облысында анықталсын . Енді осы облысты
 торымен қаптап
торымен қаптап  операторын
операторын 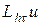 айырымдық операторымен алмастыру жолын қарастырайық. Ол үшін
айырымдық операторымен алмастыру жолын қарастырайық. Ол үшін  торының ішкі нүктелеріндегі мынандай шаблондарды алайық .
торының ішкі нүктелеріндегі мынандай шаблондарды алайық .
Егер шаблонымыз төрт нүктеден тұрса (сурет-2а) , онда
 (2.17)
(2.17)
Формулаларды ықшам түрде жазу үшін мынандай белгілеулерді енгізсек:


онда
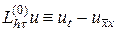 . ( 2.18)
. ( 2.18)
Мұнда біз  өрнегінің мәнін а) шаблонының төменгі нүктелерінен алдық . Ал
өрнегінің мәнін а) шаблонының төменгі нүктелерінен алдық . Ал  операторын б) шаблоны арқылы жуықтасақ, онда
операторын б) шаблоны арқылы жуықтасақ, онда
 (2.19)
(2.19)
Егер ( 2.18) және (2.19) әдістерінің сызықтық комбинациясын алсақ , онда
 (2.20)
(2.20)
 айырымдық операторда в) шаблоны қолданылады.
айырымдық операторда в) шаблоны қолданылады.
Енді осы айырымдық операторлардың жуықтау дәлдігін зерттейік . Ол үшін мына формулаларды қолданамыз:





Осы өрнектерді 
операторларына қойсақ, онда мына теңдіктерді аламыз:
1) 

2) 
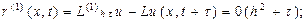

Енді жоғарыдағы дифференциалдық операторларды айырымдық функциялармен жуықтауды сипаттау үшін мынадай анықтама енгізейік:
Анықтама 1. Егер берілген  функциялар жиынының
функциялар жиынының  элементі үшін 1.
элементі үшін 1.  жағдайда
жағдайда  , ,онда
, ,онда 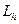 операторы
операторы  операторын жуықтайды (аппроксимациялайды) дейміз.
операторын жуықтайды (аппроксимациялайды) дейміз.
2. 
 (2.16)
(2.16)
теңсіздігі орындалса , онда 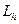 айырымдық операторы
айырымдық операторы  операторын
операторын  функциялар жиынында
функциялар жиынында  -тың
-тың  дәрежесіндегі дәлдікпен жуықтайды (аппроксимация) деп атайды .
дәрежесіндегі дәлдікпен жуықтайды (аппроксимация) деп атайды .
Әдетте  өскен сайын
өскен сайын  функциясына қойылатын талапта өсіп отырады. Мысалы
функциясына қойылатын талапта өсіп отырады. Мысалы  ,
,  айырымдық операторлары үшін
айырымдық операторлары үшін
 , ал
, ал  үшін
үшін  талабы қойылады.
талабы қойылады.
§3. Шекаралық есептерді жуықтау
(Айырымдық есептерді қою)
Осы уақытқа дейін біз жай дифференциалды операторларды айырымдық операторлармен жуықтау мәселесін қарастырдық.
Көп жағдайда дифференциалдық теңдеудің бір ғана шешуін табу үшін оған қосымша шарттар –бастапқы және шекаралық шарттар қойылады.
Айталық, дифференциалдық теңдеу
 ,
,  , (3.1)
, (3.1)
шекаралық теңдеу
 (3.2)
(3.2)
сызықты дифференциалды есебі берілсін .  облысын
облысын  торымен жауып (3.1)-(3.2) есебіндегі операторларды айырымдық операторлармен жуықтасақ, онда
торымен жауып (3.1)-(3.2) есебіндегі операторларды айырымдық операторлармен жуықтасақ, онда
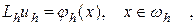 (3.3)
(3.3)
 (3.4)
(3.4)
есебін аламыз. Ал  функциялары
функциялары  тан тәуелді болғандықтан
тан тәуелді болғандықтан  ты өзгерту арқылы, шешулері
ты өзгерту арқылы, шешулері  параметріне тәуелді (3.3)- (3.4) айырымдық есептер аламыз. Осы айырымдық есептер жиынын айырымдық схема деп атаймыз.
параметріне тәуелді (3.3)- (3.4) айырымдық есептер аламыз. Осы айырымдық есептер жиынын айырымдық схема деп атаймыз.
1. Жай дифференциалдық теңдеудің Коши есебі:
Айталық,
 (3.1)
(3.1)
есебі берілсін. Бұл есепті шешу үшін  торын алайық та осы торда (3.1) есебін шешу үшін мынандай айырымдық есеп қоялық.
торын алайық та осы торда (3.1) есебін шешу үшін мынандай айырымдық есеп қоялық.

Мұндағы  болуы мүмкін .
болуы мүмкін .
Есептің жуық шешуі мына рекурентті формула арқылы табылады.

2. Бір ретті дифференциалды теңдеулер жүйесіне қойылған Коши есебі:
Есепті былайша қоямыз.
 (3.2)
(3.2)
Мұнда  квадрат матрица.
квадрат матрица. 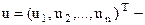 өлшемі
өлшемі  ге тең вектор. Бұл есепті шешу үшін
ге тең вектор. Бұл есепті шешу үшін  торында
торында


айырымдық схеманы пайдаланамыз, яғни 
2. Шекаралық есеп. (Дирихле есебі)
Есеп былайша қойылсын:
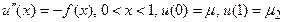 (3.3)
(3.3)
Есептің жуық шешуін табу үшін  кесіндісін
кесіндісін
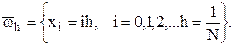
торымен жабамыз да


үш диагональді алгебралық теңдеулер жүйесімен айырбастаймыз.
Бұл теңдеулер жүйесі қуалау әдісімен шешіледі.
4. Жылу өткізгіштіктің теңдеуіне қойылған бірінші шекаралық есеп.
Бұл есеп былайша қойылады:

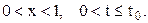
 (3.4)
(3.4)
 облысын
облысын

торымен жапсақ, онда (3.4) есебін мына


 (3.5)
(3.5)
айырымдық есебімен жуықтауға болады. Мұндағы

т.с. болуы мүмкін. (3.5) айырымдық схемасын “анықталған ” деп атайды, себебі  -ші қабатта табылған
-ші қабатта табылған  мәндері арқылы анықталады, яғни вектор түрінде жазсақ:
мәндері арқылы анықталады, яғни вектор түрінде жазсақ:

Ал анықталмаған схема былайша жазылады.
 ,
,
немесе

Біздің қарастырған мысалдарымызда шекаралық шарттар дәл алынды. Ал есепке екінші және үшінші шекаралық шарттар қойылса, онда оны жуықтау күрделі мәселе болғандықтан кейінге қалдырамыз.
5. Жылу өткішгіштік теңдеуіне қойылған аралас шекаралық есеп
Айталық, 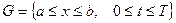 облысында
облысында
 (3.6)
(3.6)
жылу өткішгіштіктің теңдеуі және
 (3.7)
(3.7)
шекаралық шарты берілсін. Мұндағы  белгілі функциялар мен параметрлер.
белгілі функциялар мен параметрлер.  облысын
облысын
 торымен жабайық та есептің бірнеше айырымдық схемасын қарастырайық.
торымен жабайық та есептің бірнеше айырымдық схемасын қарастырайық.
1 Айқындалған схема; қолданылған шаблон 
 (3.8)
(3.8)
(жуықтау дәлдігі- 

 );
);
 (3.9)
(3.9)
(жуықтау дәлдігі-  ).
).
Схеманың жалпы дәлдігі- 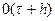 .
.
2. Айқындалмаған схема; қолданылған шаблон 
 (3.10)
(3.10)
(жуықтау дәлдігі- 

 );
);
 (3.11)
(3.11)
(жуықтау дәлдігі-  ).
).
Схеманың жалпы дәлдігі- 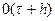 .
.
3 Крайк-Никольсон схемасы; қолданылған шаблон 
 (3.12)
(3.12)

(жуықтау дәлдігі-  ).
).
 (3.13)
(3.13)
(жуықтау дәлдігі-  ).
).
Схеманың жалпы дәлдігі-  .
.
Егер
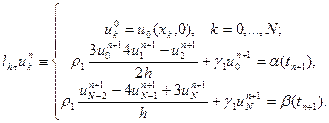 (3.14)
(3.14)
(жуықтау дәлдігі- 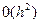 ).
).
Айырымымен жуықтасақ, онда (3.12),(3.14) схемалары (3.6), (3.7) есебін  дәлдікпен жуықтайды.
дәлдікпен жуықтайды.
§4. Айырымдық есептің шешуінің жинақталуы
туралы түсінік

Берілген есепті айырымдық есептермен алмастырғанда, осы айырымдық есептің шешуі берілген есептің шешуін қаншалықты дәл жуықтайды және торлардың қадамдарын кішірейткен сайын қандай шапшаңдықпен дәл шешімге жинақталады деген мәселені қарастырайық.
Айталық,  облысында сызықты дифференциалды теңдеу
облысында сызықты дифференциалды теңдеу
 (4.1)
(4.1)
және оның қосымша шарты
 (4.2)
(4.2)
берілсін. Мұнда  берілген функциялар ,
берілген функциялар ,  сызықты дифференциалды оператор. (4.1)-(4.2) есебінің бір ғана шешуі бар деп ұйғарамыз. Енді
сызықты дифференциалды оператор. (4.1)-(4.2) есебінің бір ғана шешуі бар деп ұйғарамыз. Енді  облысын
облысын  торымен жабайық.
торымен жабайық.  түйіндердің тығыздығын анықтайтын параметр болсын. (4.1)-(4.2) есебін
түйіндердің тығыздығын анықтайтын параметр болсын. (4.1)-(4.2) есебін
 , (4.3)
, (4.3)
 (4.4)
(4.4)
айырымдық есебімен алмастырайық. Мұндағы  белгілі торлық функциялар. (4.3)-(4.4) есебінің шешуі
белгілі торлық функциялар. (4.3)-(4.4) есебінің шешуі  торында анықталған торлық функция.
торында анықталған торлық функция.  параметрін өзгерту арқылы, яғни
параметрін өзгерту арқылы, яғни  торының тығыздығын өзгерту арқылы (4.3)-(4.4) есебінің
торының тығыздығын өзгерту арқылы (4.3)-(4.4) есебінің  тан тәуелді шешулерінің
тан тәуелді шешулерінің  жиынын аламыз.
жиынын аламыз.
(4.1)-(4.2) есебінің шешуін (4.3)-(4.4) есебінің шешуі қаншалықты жуықтайтындығын  -торлық функциялар кеңістігінде қарастырамыз.
-торлық функциялар кеңістігінде қарастырамыз.
Айталық,  функциясының
функциясының  торының түйіндеріндегі, яғни
торының түйіндеріндегі, яғни  болсын.
болсын.
Енді айырымдық схеманың шешуінің дәлдігін былай белгілесек:
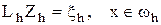 , (4.5)
, (4.5)
 (4.6)
(4.6)
есебін аламыз. Мұндағы

шамалары жуықтау қателігі (апроксимация қателігі). Яғни (4.1)-(4.2) есебін (4.3)-(4.4) есебімен алмастырғандағы жіберілген қате.
Енді  шамаларын бағалау үшін оларды тиісінше
шамаларын бағалау үшін оларды тиісінше 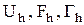 шекті өлшемді торлық функциялар жиынында жатады деп есептеп, осы жиындарда
шекті өлшемді торлық функциялар жиынында жатады деп есептеп, осы жиындарда 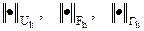 нормаларын енгізейік.
нормаларын енгізейік.
Анықтама-1 Егер  шарттары орындалса, онда (4.3)-(4.4) айырымдық схемасы (4.1)-(4.2) есебіноның шешуінде
шарттары орындалса, онда (4.3)-(4.4) айырымдық схемасы (4.1)-(4.2) есебіноның шешуінде  тың
тың  дәрежесіндегі дәлдікпен жуықтайды (аппроксимациялайды) дейді. Мұндағы
дәрежесіндегі дәлдікпен жуықтайды (аппроксимациялайды) дейді. Мұндағы 
Анықтама-2.Егер  нөлге ұмтылғанда
нөлге ұмтылғанда  нөлге ұмтылса, онда (4.3)-(4.4) есебінің шешуі (4.1)-(4.2) есебінің шешуіне жинақталады дейміз. Егер жеткілікті аз шама
нөлге ұмтылса, онда (4.3)-(4.4) есебінің шешуі (4.1)-(4.2) есебінің шешуіне жинақталады дейміз. Егер жеткілікті аз шама  табылып, және
табылып, және  болғанда
болғанда  бағалауы орындалса, онда айырымдық схеманың шешуі
бағалауы орындалса, онда айырымдық схеманың шешуі  жылдамдықпен (4.1)-(4.2) есебінің шешуіне жинақталады дейді немесе айырымдық схеманың дәлдігі
жылдамдықпен (4.1)-(4.2) есебінің шешуіне жинақталады дейді немесе айырымдық схеманың дәлдігі  -ге тең дейді. Мұндағы
-ге тең дейді. Мұндағы 
 -тан тәуелсіз сан.
-тан тәуелсіз сан.
Егер  пен
пен  ты тиісінше
ты тиісінше  пен
пен  дың
дың  торындағы
торындағы
мәндері десек, онда 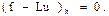 Сондықтан
Сондықтан
 Яғни (4.3)-(4.4) есебінің (4.1)-(4.2) есебін жуықтау қателігі
Яғни (4.3)-(4.4) есебінің (4.1)-(4.2) есебін жуықтау қателігі  және
және  шамаларынан тұратынын көреміз.
шамаларынан тұратынын көреміз.
Кейде (4.3)-(4.4) есебін  функциясының шекаралық (шеткі) нүктелердегі белгілі мәндерін теңдіктің оң жағына шығару арқылы,
функциясының шекаралық (шеткі) нүктелердегі белгілі мәндерін теңдіктің оң жағына шығару арқылы,
 (4.7)
(4.7)
түрінде жазуға болады. Бұл жағдайда айырымдық схеманың жуықтау қателігін былайша жазады:

Ал

теңдігін  ретті жуықтау қателігі (аппроксимациясы) дейміз.
ретті жуықтау қателігі (аппроксимациясы) дейміз.  сызықтық алгебралық теңдеулер жүйесі болғандықтан, оның шешуі
сызықтық алгебралық теңдеулер жүйесі болғандықтан, оның шешуі  қа тікелей байланысты. Сондықтан
қа тікелей байланысты. Сондықтан  жүйесінің шешуі
жүйесінің шешуі  шамасына байланысты болғандықтан,
шамасына байланысты болғандықтан,  кезде
кезде  нөлге ұмтылады ма, яғни айырымдық схеманың шешуінің дәлдігі оның берілген есепті жуықтау дәлдігімен байланысы бар ма әлде жоқ па деген сұрақ туындайды. Осы сұраққа жауап беру үшін, алдымен мына мысалды қарастырайық:
нөлге ұмтылады ма, яғни айырымдық схеманың шешуінің дәлдігі оның берілген есепті жуықтау дәлдігімен байланысы бар ма әлде жоқ па деген сұрақ туындайды. Осы сұраққа жауап беру үшін, алдымен мына мысалды қарастырайық:
1-Мысал: Айталық,
 (4.8)
(4.8)
есебі берілсін. Бұл есептің дәл шешімі

болғандықтан  Яғни
Яғни  функциясы
функциясы  бастапқы мәннен үзіліссіз тәуелді. Енді (4.8) есебін
бастапқы мәннен үзіліссіз тәуелді. Енді (4.8) есебін 
торында
 (4.9)
(4.9)
жуықтауы  айырымдық схемамен алмастырайық. Осыдан
айырымдық схемамен алмастырайық. Осыдан
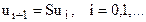


немесе
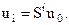
Енді бір 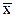 нүктесін таңдап алайық та
нүктесін таңдап алайық та  қадамын, осы нүкте түйін нүктесі болып қала беретіндей етіп, нөлге ұмтылдырайық.
қадамын, осы нүкте түйін нүктесі болып қала беретіндей етіп, нөлге ұмтылдырайық.

болса, онда  нөлге ұмтылған сайын
нөлге ұмтылған сайын  шексіз өсіп отырады. Сондықтан
шексіз өсіп отырады. Сондықтан

Ал 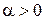 болғандықтан кез-келген
болғандықтан кез-келген  үшін
үшін 
 болу себепті
болу себепті
 (4.10)
(4.10)
және


болғандықтан айырымдық схеманың шешуі (4.8) есебінің шешуіне
жинақталады.
Енді осы (4.8) есебін  торында
торында  дәлдікпен жуықтайтын мына айырымдық схеманы қарастырайық:
дәлдікпен жуықтайтын мына айырымдық схеманы қарастырайық:
 (4.11)
(4.11)

Осыдан


немесе

Ал 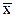 түйінінде
түйінінде
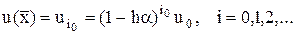
Енді қандай жағдайда (4.11) айырымдық схеманың шешуі (4.8) есебінің шешуіне жинақталатынын қарастырайық.
1-жағдай.  қадамының мәндерін
қадамының мәндерін 
шарты орындалатындай етіп таңдасақ, онда
 (4.12)
(4.12)
және

яғни (4.11) айырымдық схемасының шешуі (4.8) есебінің шешуіне жинақталады.
2-жағдай.  болсын. Онда
болсын. Онда  шешуі
шешуі  өскен сайын өсіп отырады, яғни (4.8) есебінің шешуіне жинақталмайды. Осыдан айырымдық схеманың шешуінің жинақтылығы айырымдық схеманың берілген есепті жуықтау дәлдігімен байланысты бола бермейтіндігін көреміз. Мұның себебіне келесі параграфта тоқталамыз.
өскен сайын өсіп отырады, яғни (4.8) есебінің шешуіне жинақталмайды. Осыдан айырымдық схеманың шешуінің жинақтылығы айырымдық схеманың берілген есепті жуықтау дәлдігімен байланысты бола бермейтіндігін көреміз. Мұның себебіне келесі параграфта тоқталамыз.
§5. Айырымдық схеманың орнықтылығы
туралы түсінік
Дифференциалды есепті айырымдық схемамен алмастырған кезде шыққан

сызықты теңдеулер жүйесінің оң жағы белгілі бір қателіктермен беріледі (бастапқы және шекаралық шарттарды пайдаланған кезде жіберілген қателер). Және осы теңдеулер жүйесін шешкен кезде қателер жіберілуі мүмкін (дөңгелектенген кезде, басқа да кездейсоқ қателер). Егер айырымдық схеманы шешу кезінде бастапқы қателер өсетін болса, ондай схемалар іс жүзінде жарамсыз болып табылады.
Ондай айырымдық схемаларды орнықсыз схемалар деп атайды. Ал, егер айырымдық схеманы шешкен кезде бастапқы қателер өспейтін болса, онда ондай схемаларды орнықты схемалар дейміз. Мысалы (4.9) айырымдық схемасы бастапқы мәннен үзіліссіз тәуелді екенін, яғни бастапқы мән бойынша орнықты екенін көреміз. Ал (4.11) айырымдық схемасы  шарты орындалған кезде орнықсыз, яғни
шарты орындалған кезде орнықсыз, яғни  нөлге ұмтылғанда шексіздікке ұмтылатынын көрдік. Енді айырымдық схемалардың қай уақытта орнықты екенін айқындайтын анықтамалар енгізейік.
нөлге ұмтылғанда шексіздікке ұмтылатынын көрдік. Енді айырымдық схемалардың қай уақытта орнықты екенін айқындайтын анықтамалар енгізейік.
1-анықтама. Егер  сандары табылып,
сандары табылып,  орындалғанда кез-келген
орындалғанда кез-келген  үшін
үшін
 (5.1)
(5.1)
айырымдық есебінің бір ғана шешуі бар болып,
 (5.2)
(5.2)
теңсіздігі орындалса, онда
 (5.3)
(5.3)
айырымдық схемасын орнықты дейміз. Мұндағы  тан тәуелсіз тұрақты сан.
тан тәуелсіз тұрақты сан.
(5.2) теңсіздігі (5.3) айырымдық схемасының оң жағына  өсімше берсек, онда оның шешуі
өсімше берсек, онда оның шешуі  бойынша бірқалыпты
бойынша бірқалыпты
аз шамаға өзгеретінін көрсетеді.
Егер  операторы
операторы  -ты
-ты  қа кескіндейтін сызықты оператор болса, онда жоғарғы анықтамаға пара-пар мына анықтаманы беруге болады.
қа кескіндейтін сызықты оператор болса, онда жоғарғы анықтамаға пара-пар мына анықтаманы беруге болады.
2-анықтама. Егер кез-келген 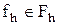 үшін
үшін  сызықты айырымдық есебінің бір ғана шешуі-
сызықты айырымдық есебінің бір ғана шешуі- 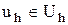 бар болып,
бар болып,
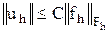 (5.4)
(5.4)
теңсіздігі орындалса, онда айырымдық есепті орнықты дейміз.
Мұндағы  қа тәуелсіз тұрақты сан.
қа тәуелсіз тұрақты сан.
Екі анықтамадағы С саны  тың тек белгілі бір мәнінде ғана тұрақты сан болса, онда мұндай айырымдық схеманы шартты орнықты, ал кез-келген
тың тек белгілі бір мәнінде ғана тұрақты сан болса, онда мұндай айырымдық схеманы шартты орнықты, ал кез-келген  үшін тұрақты болса шартсыз (абсолют) орнықты дейді.
үшін тұрақты болса шартсыз (абсолют) орнықты дейді.
Енді  сызықты оператор болған жағдайда екі анықтаманың бір-біріне баламалы екенін көрсетейік.
сызықты оператор болған жағдайда екі анықтаманың бір-біріне баламалы екенін көрсетейік.
Алдымен сызықтық айырымдық схеманың 2-анықтама бойынша орнықты болса, онда 1-анықтама бойынша да орнықты екенін көрсетейік. Айталық, барлық  және кез-келген
және кез-келген 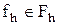 үшін (5.3) схемасының бір ғана шешуі бар және (5.4) бағалауы орындалсын. Енді (5.1) теңдіктен (5.3) теңдігін алып тастасақ, онда
үшін (5.3) схемасының бір ғана шешуі бар және (5.4) бағалауы орындалсын. Енді (5.1) теңдіктен (5.3) теңдігін алып тастасақ, онда

теңдігін аламыз. Осы теңдікке (5.4) бағалауын қолдансақ (5.2) бағалауын аламыз, яғни схема 1-анықтама бойынша орнықты .
Енді айырымдық схеманың 1-анықтама бойынша орнықты болса, онда 2-анықтама бойынша да орнықты екенін көрсетейік. 1-анықтама бойынша  бар болып,
бар болып,  және
және  шамалары үшін
шамалары үшін
 , (5.5)
, (5.5)
 (5.6)
(5.6)
теңдеулерінің бір ғана шешуі бар.
Егер  десек, онда (5.5) теңдеуінен (5.6) теңдеуін алу арқылы
десек, онда (5.5) теңдеуінен (5.6) теңдеуін алу арқылы
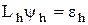 (5.7)
(5.7)
теңдеуін аламыз. Осыдан (5.2) бағалауын ескерсек
 . (5.8)
. (5.8)
Егер (5.7) теңдеуінің оң жағын және шешуін өзгертсек, онда соңғы алынған бағалауға кез келген 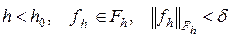 үшін (5.3) есебінің бірғана шешуі
үшін (5.3) есебінің бірғана шешуі  бар екенін және (5.4) бағалауы орындалатындығын тұжырымдауға болады.
бар екенін және (5.4) бағалауы орындалатындығын тұжырымдауға болады.
Шынында да,  болсын деп, (5.3) есебінің бірғана шешуі бар және (5.4) бағалауы орындалатынын дәлелдейік.
болсын деп, (5.3) есебінің бірғана шешуі бар және (5.4) бағалауы орындалатынын дәлелдейік.
Айталық,  болсын, онда
болсын, онда
 (5.9)
(5.9)

болғандықтан (5.9) есебінің бірғана шешуі бар және

Сондықтан  пен
пен 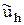 және
және  пен
пен  өзара байланысты болғандықтан кез-келген
өзара байланысты болғандықтан кез-келген  үшін (5.3) есебінің бір ғана шешуі бар және (5.4) бағалауы орындалады.
үшін (5.3) есебінің бір ғана шешуі бар және (5.4) бағалауы орындалады.
Қорыта келгенде  теңдеуінің шешуі бар дегеніміз
теңдеуінің шешуі бар дегеніміз  бар болып
бар болып

орындалады, ал схеманың орнықты дегеніміз  операторы
операторы  бойынша бірқалыпты шектелген, яғни
бойынша бірқалыпты шектелген, яғни

деген сөз. Мұндағы  тан тәуелсіз сан. Басқаша айтқанда, орнықты дегеніміз- (5.3) теңдеуінің шешуі теңдеудің оң жағынан үзіліссіз тәуелді болуы. Және бұл тәуелділік
тан тәуелсіз сан. Басқаша айтқанда, орнықты дегеніміз- (5.3) теңдеуінің шешуі теңдеудің оң жағынан үзіліссіз тәуелді болуы. Және бұл тәуелділік  бойынша бірқалыпты болуы керек.
бойынша бірқалыпты болуы керек.
Сонымен (5.3) теңдеуі орнықты болса, онда оның оң жағының аз ғана өзгеруін сәйкес теңдеудің шешуіде аз шамаға өзгереді. Орнықтылық-айырымдық схеманың кездейсоқ қателерге сезімталдығы және ол айырымдық схеманың ішкі қасиеті болып табылады. Оның бастапқы дифференциалды теңдеумен ешқандай байланысы жоқ.
Ескерту. Егер айырымдық есепті
 (5.10)
(5.10)
(дифференциалдық теңдеудің айырымдық схемасы)
 (5.11)
(5.11)
(шекаралық шарттың айырымдық схемасы) түрінде берілсе, онда айырымдық есептің орнықтылығының анықтамасын былайша да беруге болады.
3-анықтама . Егер (5.10)-(5.11) айырымдық есебінің  шешімі үшін
шешімі үшін

бағалауы орындалса, онда айырымдық схема орнықты деп аталады. Себебі (5.10)-(5.11) есебін былайша жазуға болатындықтан:
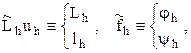

3-анықтама 2-анықтамаға пара-пар.
§6. Айырымдық есептің жинақталуы туралы теорема
Айталық,
 (6.1)
(6.1)
айырымдық схемасы
 (6.2)
(6.2)
шекаралық есебін  шешуі бойынша
шешуі бойынша  дәлдікпен жуықтайтын болсын. Яғни (6.2) теңдеуінің шешуін (6.1) теңдеуіне қойсақ, онда
дәлдікпен жуықтайтын болсын. Яғни (6.2) теңдеуінің шешуін (6.1) теңдеуіне қойсақ, онда
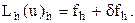
Осыдан
 . (6.3)
. (6.3)
Мұндағы  тан тәуелсіз тұрақты сан. Енді (6.1) айырымдық есебінің жуықтау дәлдігімен оның орнықтылығының және
тан тәуелсіз тұрақты сан. Енді (6.1) айырымдық есебінің жуықтау дәлдігімен оның орнықтылығының және  шешуінің (6.2) теңдеуінің шешуіне жинақталуының арасындағы байланысы, яғни жуықтау дәлдігі мен орнықтылықтан жинақтылық шарты орындалатынын көрсететін теореманы дәлелдейік.
шешуінің (6.2) теңдеуінің шешуіне жинақталуының арасындағы байланысы, яғни жуықтау дәлдігі мен орнықтылықтан жинақтылық шарты орындалатынын көрсететін теореманы дәлелдейік.
Теорема.  айырымдық схемасы
айырымдық схемасы 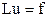 есебін
есебін  дәлдікпен жуықтайтын және орнықты болса, онда
дәлдікпен жуықтайтын және орнықты болса, онда  шешуі
шешуі 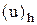 шешуіне жинақталады және
шешуіне жинақталады және
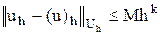 (6.4)
(6.4)
бағалауы орындалады.
Дәлелдеуі. Егер  десек, онда (5.2) бағалауы
десек, онда (5.2) бағалауы

түрінде жазылады. Енді (6.3) теңсіздігін ескерсек, онда
 ,
,
мұндағы 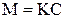 теорема дәлелденді.
теорема дәлелденді.
Қорытындысында мынаны ескерген жөн:
1.  сызықты айырымдық есебінің шешуі
сызықты айырымдық есебінің шешуі  теңдеуінің шешуіне жинақталатынын тексеру үшін
теңдеуінің шешуіне жинақталатынын тексеру үшін  теңдеуінің орнықтылығымен жуықтау дәлдігін анықтау жеткілікті. Мұнда
теңдеуінің орнықтылығымен жуықтау дәлдігін анықтау жеткілікті. Мұнда  есебі тек дифференциалды теңдеудің шекарадық есебі емес, кез-келген функционалды теңдеу болуы мүмкін. Ол тек
есебі тек дифференциалды теңдеудің шекарадық есебі емес, кез-келген функционалды теңдеу болуы мүмкін. Ол тек  айырымдық есебінің конструкциясын жасау үшін ғана қажетті.
айырымдық есебінің конструкциясын жасау үшін ғана қажетті.
2.  айырымдық есебінің шешуінің жинақтылығын анықтау
айырымдық есебінің шешуінің жинақтылығын анықтау  кеңістіктерінде алынған нормаларға тікелей байланысты. Көбінесе
кеңістіктерінде алынған нормаларға тікелей байланысты. Көбінесе  кеңістігіндегі норманы
кеңістігіндегі норманы
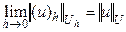 (6.5)
(6.5)
теңдігі орындалатындай етіп алады.
Мысалы.  үзіліссіз функциялар кеңістігі болса және осы кеңістіктегі
үзіліссіз функциялар кеңістігі болса және осы кеңістіктегі  функциясының нормасын былайша анықтасақ
функциясының нормасын былайша анықтасақ
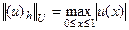
онда торлық функцияның нормасын
 , (6.6)
, (6.6)
санымен анықтаған дұрыс. Себебі
 .
.
Егер үзіліссіз функцияның нормасын былайша алсақ,
 (6.7)
(6.7)
онда торлық функцияның нормасын былайша
 (6.8)
(6.8)
алуға болады.  үзілісті бірақ квадраты бойынша интегралданатын болса, оның нормасын былайша аламыз.
үзілісті бірақ квадраты бойынша интегралданатын болса, оның нормасын былайша аламыз.
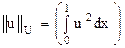
Бұл жағдайда торлық функцияның нормасын (6.8) арқылы аламыз да, оның мәнін
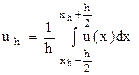
формуласы бойынша анықтаймыз. Кейде функцияның өзгеру жылдамдығын ескертіп

нормасын қолданады, онда торлық функцияның нормасын былайша

алуға болады. Бұл жағдайда да (6.5) теңдігі орындалады. т.с. бұдан да басқа нормаларды пайдалануға болады.
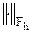 нормасын
нормасын  нормасынан тәуелсіз әртүрлі жолмен алуға болады. Бірақ
нормасынан тәуелсіз әртүрлі жолмен алуға болады. Бірақ 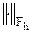 нормасын таңдаған кезде айырымдық есептің орнықтылығымен қоса оның жуықтау дәлдігі жоғары болатындай етіп алуға тырысқан дұрыс.
нормасын таңдаған кезде айырымдық есептің орнықтылығымен қоса оның жуықтау дәлдігі жоғары болатындай етіп алуға тырысқан дұрыс.
Шынында да, егер 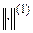 нормасы бойынша
нормасы бойынша  схемасы
схемасы
 есебін
есебін  шешуі бойынша
шешуі бойынша  дәлдікпен жуықтасын және орнықты болсын. Онда жинақталу теоремасы бойынша
дәлдікпен жуықтасын және орнықты болсын. Онда жинақталу теоремасы бойынша
 . (6.9)
. (6.9)
Яғни
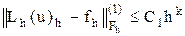 (6.10)
(6.10)
- схеманың жуықтау дәлдігі,
 (6.11)
(6.11)
- орнықтылығы.
Егер 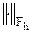 нормасын былайша алсақ,
нормасын былайша алсақ,
 , (6.12)
, (6.12)
онда
 (6.13)
(6.13)
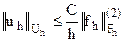 . (6.14)
. (6.14)
Бұл жағдайда схеманың жуықтау дәлдігі  болғанымен,
болғанымен,
схеманың орнықтылығы жоғалады. Себебі


Егер  нормасын былайша алсақ:
нормасын былайша алсақ:
 (6.15)
(6.15)
онда
 (6.16)
(6.16)
 (6.17)
(6.17)
Мұнда (6.17) теңсіздік схеманың орнықтылығын көрсеткенмен, жуықтау дәлдігі бір дәрежеге кемігенін көреміз. Және де айырымдық схеманың жуықтау дәлдігімен орнықтылығы орындалатындай норманы таңдау, кейбір жағдайда, мүмкін емес. Себебі бұл жағдайда кез келген айырымдық схема жинақты болар еді. Мысалы (4.11) айырымдық схемасы үшін  болған жағдайда жинақтылық шарты орындалатындай норма табуға болмайды.
болған жағдайда жинақтылық шарты орындалатындай норма табуға болмайды.
§7. Айырымдық схемалардың орнықтылығын
Зерттеу жолдары
Орнықтылық-айырымдық схемалар теориясындағы негізгі мәселелердің бірі болып табылады. Орнықтылық анықтамасын әртүрлі жолмен анықтағанмен олардың негізі біреу. Ол-айырымдық схеманың шешуінің тордың қадамы бойынша, берілген есептің бастапқы мәндерінен бірқалыпты үзіліссіз тәуелді болуы. Орнықтылықты оның айырымдық схеманың дәлдігімен байланысы жоқ болғандықтан, жеке зерттеуге болады.
Енді берілген айырымдық схеманың орнықтылығын анықтаудың кейбір жолдарымен танысайық.
7.1. Коши есебін айырымдық есеп бойынша есептегендегі орнықтылықтың жеткілікті шарты.
Айталық, 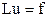 есебі
есебі  айырымдық есебімен жуықталды делік. Ал тор нүктелеріндегі есептің дәл шешуін
айырымдық есебімен жуықталды делік. Ал тор нүктелеріндегі есептің дәл шешуін  деп белгілейік.
деп белгілейік. 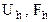 сызықты нормаланған кеңістіктер және
сызықты нормаланған кеңістіктер және 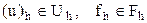 болсын.
болсын.
Егер айырымдық схема орнықты болса, онда  есебінің бір ғана шешуі бар және кез-келген
есебінің бір ғана шешуі бар және кез-келген  үшін
үшін

теңсіздігі орындалуы керек.
Коши есебін шешкен кезде торлық  функциясын біртіндеп табады, яғни бір нүктедегі
функциясын біртіндеп табады, яғни бір нүктедегі  мәнін тапқаннан кейін келесі көрші нүктедегі
мәнін тапқаннан кейін келесі көрші нүктедегі  мәнін табады. Осы процесс кезінде
мәнін табады. Осы процесс кезінде  шешуінің өсуін жоғарыдан бағалай алсақ, онда айырымдық схеманың орнықтылығын айқындай аламыз.
шешуінің өсуін жоғарыдан бағалай алсақ, онда айырымдық схеманың орнықтылығын айқындай аламыз.
1-Мысал.
 (7.1)
(7.1)
есебін
 (7.2)
(7.2)
айырымдық есебімен айырбастасақ, онда осы айырымдық есепті былайша жазуға болады:
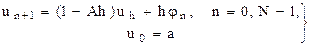 (7.3)
(7.3)
Осыдан

Енді  кеңістіктерінде мынандай нормаларды анықтасақ:
кеңістіктерінде мынандай нормаларды анықтасақ:
 (7.5)
(7.5)
 (7.6)
(7.6)
және  үшін
үшін
 (7.7)
(7.7)
теңсіздігін ескерсек, онда

Ал 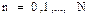 кез келген натурал сан екенін ескерсек, онда
кез келген натурал сан екенін ескерсек, онда

яғни айырымдық есептің орнықты екенін көреміз. Егер мынандай белгілеулер енгізсек: