 |
|
Плотность вероятности. Числовые характеристики непрерывных случайных величин.
1. Дана интегральная функция непрерывной случайной величины 
:
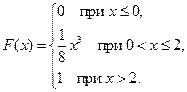
Найти плотность вероятности 
, построить график этой функции и найти вероятность того, что в результате испытания случайная величина примет значение в интервале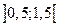 
.
2. Плотность вероятности случайной величины имеет вид:
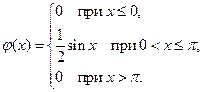
Построить график функции и на основе исследования графика показать, что вероятности попадания случайной величины в интервалы 
и 
равны между собой, найти математическое ожидание случайной величины.
3. Дана плотность вероятности непрерывной случайной величины :
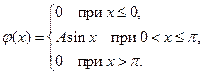
Найти интегральную функцию 
, предварительно вычислив значение параметра 
.
4. Случайная величина задана плотностью вероятности 
в интервале 
, вне этого интервала 
. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины .
5. Случайная величина задана плотностью вероятности 
в интервале 
, вне этого интервала . Найти математическое ожидание и дисперсию случайной величины 
.
6. Дана интегральная функция непрерывной случайной величины :
Найти плотность вероятности .
7. Дана интегральная функция непрерывной случайной величины :
Найти плотность вероятности .
8. Дана интегральная функция непрерывной случайной величины :
Найти плотность вероятности . Вычислить вероятность того, что случайная величина попадет в интервал 
двумя способами: 1) используя свойства интегральной функции; 2) используя свойства функции .
9. Плотность вероятности случайной величины имеет вид:
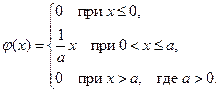
Найти параметр 
. Построить график функции и на основе исследования графика найти вероятность того, что в результате испытания случайная величина примет значение в интервале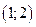 
.
10. Дана плотность вероятности случайной величины :
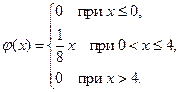
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины . Найти вероятность того, что в результате испытания случайная величина примет значение в интервале 1) 
; 2) или в интервале 
.
11. Случайная величина , принимающая положительные значения, имеет плотность вероятности 
. Найти границы значений случайной величины , параметр и математическое ожидание случайной величины .
12. Случайная величина имеет плотность вероятности
Найти интегральную функцию F(x), построить ее график и определить по графику вероятность того, что случайная величина примет значение в интервале 
.
13. Дана плотность вероятности случайной величины :
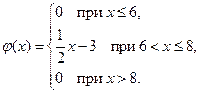
Найти интегральную функцию F(x).
14. Дана плотность вероятности случайной величины :
Найти параметр А.
15. Дана плотность вероятности случайной величины :
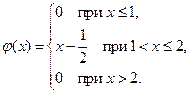
Найти математическое ожидание и дисперсию случайной величины 
.
16. Случайная величина задана плотностью вероятности
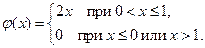
Найти математическое ожидание и дисперсию случайной величины 
.