Безумовна оптимізація

Домашня робота

ДОСЛІДЖЕННЯ МЕТОДІВ БЕЗУМОВНОЇ ОПТИМІЗАЦІЇ ОДНОВИМІРНИХ ТА БАГАТОВИМІРНИХ ФУНКЦІЙ

Мета роботи –вивчити методи безумовної оптимізації одновимірних та багатовимірних функцій.

Теоретичні відомості

Безумовна оптимізація

Задача оптимізації формулюється таким чином: задані множина Х (допустима множина задачі) і функція f (x) (цільова функція), визначена на Х; необхідно знайти точки мінімуму або максимуму функції f на Х. Задача оптимізації, в якій цільову функцію необхідно мінімізувати, має вигляд

Розрізняють необхідні умови оптимальності, тобто умови, яким має відповідати точка, яка є розв’язком задачі, і достатні умови оптимальності, тобто умови, з яких випливає, що ця точка є розв’язком задачі.

Необхідна умова локальної оптимальності для функції однієї змінної. Нехай f (x) диференційована в точці x*∈R1. Якщо x* – точка локального оптимуму (екстремуму), то

f ′(x*) = 0. (2.1)

Точки, що відповідають умові (2.1), називаються стаціонарними. Стаціонарні точки можуть бути точками локального мінімуму, максимуму або перегину. Для визначення характеру стаціонарних точок використовується достатня умова локальної оптимальності.

Достатня умова локальної оптимальності. Нехай f (x), k разів (k>1) диференційована в точці x* ∈ R1, причому

f ′(x*) = f ′′(x*) = ... = f ^{(k −1)} (x*) = 0, f ^(k) (x*) ≠ 0.

Тоді, якщо k − парне число, то x* − точка локального мінімуму при f ^{(k )}(x*) > 0 або максимуму при f ^{(k )}(x*) < 0 . Якщо k − непарне число, то x* − точка перегину.

Для функції f(x) багатьох змінних точка x являє собою вектор, f ′(x) − вектор перших часткових похідних функції f(x) (градієнт – Grad f (x)).

Необхідна умова локальної оптимальності. Нехай f(x) диференційована в точці x* ∈ R_n . Якщо x* − точка локального екстремуму, то f ′(x*) = 0.

Алгоритм визначення точок локальних екстремумів функції багатьох змінних:

1) знаходимо f ′(x);

2) розв’язуємо систему ;

3) обчислюємо стаціонарніточки x(i) , i =1,N;

4) обчислюємо значення функції в цих точках и обираємо мінімальне.

Приклад. Визначити мінімум цільової функції, заданої виразом . Побудувати графік функції поблизу точки екстремуму.

Розв’язання.

1. Знаходимо f′(x), тобто градієнт функції .

2. Розв’язуємо систему:

3. Розв’язок досягається за стаціонарних точок , , .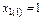

4. Значення функції в цих точках , .

Таким чином, мінімум досягається в точці , .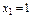

Використовуючи програму Excel, будуємо графік цільової функції спочатку за однією з координат, зафіксувавши другу в мінімуму (наприклад, а змінюється від –2 до 2, (рис. 2.1)), потім за фіксованого змінюється (рис. 2.2).

Рис. Графік функції за координатою x₁.

Рис. Графік функції за координатою x₂.