 |
|
Комплексні числа та дії над ними
1.1. Поняття комплексного числа
Комплексним числом (в алгебраїчній формі) називається вираз
 ,
,
де  – дійсні числа;
– дійсні числа;  – уявна одиниця,
– уявна одиниця,  ,
,  .
.
Числа  і
і  називаються відповідно дійсною і уявною частинами комплексного числа
називаються відповідно дійсною і уявною частинами комплексного числа  . Позначаються
. Позначаються
 .
.
Множина всіх комплексних чисел позначається  .
.
Будь-яке дійсне число  можна розглядати як комплексне число
можна розглядати як комплексне число  , у якого уявна частина дорівнює нулю:
, у якого уявна частина дорівнює нулю: 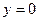 . Таким чином, множина дійсних чисел
. Таким чином, множина дійсних чисел  є підмножиною множини комплексних чисел
є підмножиною множини комплексних чисел  :
:  .
.
Комплексне число  , у якого дійсна частина дорівнює нулю, а уявна частина відмінна від нуля, називається чисто уявним.
, у якого дійсна частина дорівнює нулю, а уявна частина відмінна від нуля, називається чисто уявним.
Два комплексних числа  і
і  називаются рівними, якщо відповідно рівні їх дійсні та уявні частини:
називаются рівними, якщо відповідно рівні їх дійсні та уявні частини:
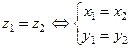 .
.
Комплексне число рівне нулю 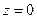 , якщо рівні нулю його дійсна та уявна частини:
, якщо рівні нулю його дійсна та уявна частини:
 .
.
Зауваження. Для комплексних чисел не існують поняття “більше”, “менше”.
Комплексне число  називається протилежним до числа
називається протилежним до числа  .
.
Два комплексних числа  і
і 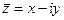 , у яких дійсні частини однакові, а уявні відрізняються тільки знаком, називаются комплексно спряженими. Очевидно, що
, у яких дійсні частини однакові, а уявні відрізняються тільки знаком, називаются комплексно спряженими. Очевидно, що 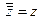 .
.
1.2. Дії над комплексними числами в алгебраїчній формі
Операції додавання, віднімання, множення, ділення і піднесення до натурального степеня здійснюються за правилами дій над многочленами з врахуванням умови  і зведенням подібних.
і зведенням подібних.
Зокрема, додавання і віднімання комплексних чисел  і
і  здійснюються покомпонентно:
здійснюються покомпонентно:
 ;
;  .
.
Множення комплексних чисел  і
і  здійснюється за правилом множення двочленів з урахуванням умови
здійснюється за правилом множення двочленів з урахуванням умови  і зведенням подібних:
і зведенням подібних:
 .
.
Зауваження 1. Для множення комплексного числа  на дійсне число
на дійсне число  досить кожну його компоненту помножити на це число
досить кожну його компоненту помножити на це число  :
:  .
.
Зауваження 2. Знайдемо натуральні степені уявної одиниці:  . Отже
. Отже
 .
.
Зауваження 3. При піднесенні комплексного числа до натурального степеня можна застосовувати відомі з елементарної математики формули скороченого множення.
Зауваження 4. Сума і добуток двох комплексно спряжених чисел  і
і 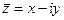 є дійсним числом:
є дійсним числом:
 ;
; 
Зауваження 5. Дійсну і уявну частини комплексного числа  можна виразити через саме число та йому спряжене
можна виразити через саме число та йому спряжене 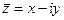 :
:
 ;
;  .
.
Ділення комплексних чисел  і
і  ,
,  виконується так: 1) треба чисельник і знаменник дробу
виконується так: 1) треба чисельник і знаменник дробу  домножити на число
домножити на число 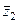 , спряжене до знаменника
, спряжене до знаменника  ; 2) врахувати, що
; 2) врахувати, що  , і звести подібні; 3) почленно розділити чисельник на знаменник і одержати частку в алгебраїчній формі.
, і звести подібні; 3) почленно розділити чисельник на знаменник і одержати частку в алгебраїчній формі.
 .
.
Зауваження 6. Основні властивості розглянутих арифметичних операцій над комплексними числами співпадають з відповідними властивостями аналогічних операцій над дійсними числами. Тому для комплексних чисел залишаються справедливими всі теореми, правила, формули, що виведені для дійсних чисел на підставі цих властивостей.
Приклад. Виконати дії над комплексними числами в алгебраїчній формі:
 .
.
Розв’язання. Виконуємо дії як над многочленами:





 .
.
1.3. Геометрична інтерпретація. Модуль і аргумент
комплексного числа
Якщо на площині введено прямокутну декартову систему координат  , то між множиною всіх точок цієї площини і множиною комплексних чисел
, то між множиною всіх точок цієї площини і множиною комплексних чисел  можна встановити взаємно однозначну відповідність: кожному комплексному числу
можна встановити взаємно однозначну відповідність: кожному комплексному числу  відповідає єдина точка
відповідає єдина точка  і навпаки (рис. 1). Дійсні числа зображаються точками осі абсцис
і навпаки (рис. 1). Дійсні числа зображаються точками осі абсцис 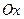 , тому вісь
, тому вісь 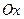 називається дійсною віссю. Чисто уявні числа зображаються точками осі ординат
називається дійсною віссю. Чисто уявні числа зображаються точками осі ординат 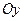 , тому вісь
, тому вісь 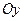 називається уявною віссю. Числу
називається уявною віссю. Числу 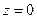 відповідає початок координат
відповідає початок координат  .
.
 Координатна площина
Координатна площина  , яка зображає множину всіх комплексних чисел
, яка зображає множину всіх комплексних чисел  , називається комплексною площиною
, називається комплексною площиною  або
або  -площиною.
-площиною.
Зауваження 1. Комплексне число  можна також зобразити радіус-вектором
можна також зобразити радіус-вектором  , що виходить із початку координат
, що виходить із початку координат  і закінчується в точці
і закінчується в точці  (рис. 1).
(рис. 1).
 Зауваження 2. Додавання і віднімання комплексних чисел можна здійснювати за правилами (трикутника і паралелограма) відповідних операцій над векторами (рис. 2). Множення комплексних чисел можна розглядати як ще один вид (поряд зі скалярним і векторним) добутку плоских векторів.
Зауваження 2. Додавання і віднімання комплексних чисел можна здійснювати за правилами (трикутника і паралелограма) відповідних операцій над векторами (рис. 2). Множення комплексних чисел можна розглядати як ще один вид (поряд зі скалярним і векторним) добутку плоских векторів.
Якщо на комплексній площині (рис. 1) ввести також полярну систему координат 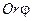 з полюсом у початку декартової системи координат і полярною віссю, суміщеною з віссю
з полюсом у початку декартової системи координат і полярною віссю, суміщеною з віссю 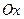 , то точку
, то точку  , що зображає комплексне число
, що зображає комплексне число  можна задати полярними координатами
можна задати полярними координатами  .
.
Полярний радіус 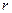 (довжина радіус-вектора
(довжина радіус-вектора  ) називається модулем комплексного числа
) називається модулем комплексного числа  і позначається
і позначається  .
.
Очевидно, що  .
.
Полярний кут  (кут між радіус-вектором
(кут між радіус-вектором  і полярною віссю
і полярною віссю 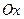 ) називається аргументом комплексного числа
) називається аргументом комплексного числа  і позначається
і позначається  .
.
Аргумент  , як кут повороту, визначається з точністю до сталого доданку вигляду
, як кут повороту, визначається з точністю до сталого доданку вигляду  (довільного числа повних обертів).
(довільного числа повних обертів).
Єдине значення  , що задовольняє умову
, що задовольняє умову  , називається головним значенням аргументу і позначається
, називається головним значенням аргументу і позначається  .
.
Отже, 
Головне значення аргументу визначається за формулою:
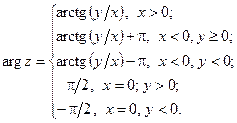
Зауваження 3. Для числа 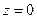 модуль дорівнює нулю
модуль дорівнює нулю 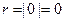 , а аргумент
, а аргумент  довільний.
довільний.
Зауваження 4. У рівних комплексних чисел  модулі також рівні
модулі також рівні  , а аргументи зв’язані співвідношенням
, а аргументи зв’язані співвідношенням  ,
,  , тобто відрізняються на доданок
, тобто відрізняються на доданок  .
.
1.4. Тригонометрична і показникова форми
комплексного числа
Використовуючи зв’язок декартових і полярних координат  ,
, 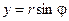 , комплексне число
, комплексне число  можна подати у вигляді
можна подати у вигляді
 .
.
Вираз  називається тригонометричною формою комплексного числа.
називається тригонометричною формою комплексного числа.
Перехід від алгебраїчної до тригонометричної форми задається співвідношеннями:
 ;
;  ;
;  .
.
Якщо звернутись до основної формули Ейлера
 ,
,
(її доведення дається в теорії рядів), то від тригонометричної форми можна перейти до показникової форми комплексного числа  .
.
Зауваження. З основної формули Ейлера випливають допоміжні формули Ейлера:
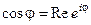 ;
; 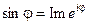 ;
;
 ;
;  .
.
Приклад 1. Довести тотожність:
 .
.
Розв’язання. Перейдемо до експонент, скористаємося формулою часткової суми геометричної прогресії, потім від експонент повернемось до тригонометричних функцій:



 .
.
Приклад 2. Зобразити на комплексній площині і подати в тригонометричній та показниковій формах наступні комплексні числа, що задані в алгебраїчній формі:
 ;
;  ;
;  ;
;  ;
;  .
.
 Розв’язання. Побудуємо задані числа на комплексній площині (рис. 3):
Розв’язання. Побудуємо задані числа на комплексній площині (рис. 3):
Знайдемо модуль і головне значення аргументу кожного з даних чисел та запишемо їх у тригонометричній та показниковій формах:
 :
:
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 :
: 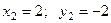 ;
;  ;
;
 ;
;  ;
;
 .
.
 :
:  ;
;  ;
;
 ;
;
 .
.
 :
:  ;
;  ;
;
 ;
;
 ;
;  .
.
 :
:  ;
;  ;
;
 ;
;
 ;
;  ;
;
 .
.
1.5. Дії над комплексними числами
в тригонометричній і показниковій формах
Якщо  і
і  – два комплексні числа в тригонометричній формі, то їх добуток:
– два комплексні числа в тригонометричній формі, то їх добуток:
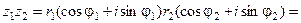
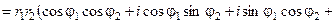
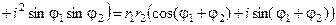 .
.
Добутком двох комплексних чисел  і
і  є комплексне число, модуль якого дорівнює добутку модулів, а аргумент – сумі аргументів співмножників.
є комплексне число, модуль якого дорівнює добутку модулів, а аргумент – сумі аргументів співмножників.
Отже,
 ;
;  ;
;
 ;
;  .
.
Якщо  і
і  – два комплексні числа в тригонометричній формі, причому
– два комплексні числа в тригонометричній формі, причому  відмінне від нуля
відмінне від нуля  , то їх частка:
, то їх частка:


 .
.
Часткою  двох комплексних чисел
двох комплексних чисел  і
і  , де дільник
, де дільник  , є комплексне число, модуль якого дорівнює частці модулів діленого
, є комплексне число, модуль якого дорівнює частці модулів діленого  і дільника
і дільника  , а аргумент – різниці аргументів діленого
, а аргумент – різниці аргументів діленого  і дільника
і дільника  .
.
Отже,
 ;
;  ;
;
 ;
;  .
.
Натуральним степенем  комплексного числа
комплексного числа  називається комплексне число, отримане множенням числа
називається комплексне число, отримане множенням числа  самого на себе
самого на себе 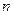 раз, де
раз, де 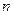 – натуральне число.
– натуральне число.
Із правила множення комплексних чисел в тригонометричній формі випливає перша формула Муавра:
 .
.
Коренем 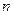 -го степеня
-го степеня  з комплексного числа
з комплексного числа  називається таке комплексне число,
називається таке комплексне число, 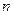 -й степінь якого дорівнює
-й степінь якого дорівнює  :
:
Очевидно, що корінь 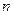 -го степеня з нуля дорівнює нулю.
-го степеня з нуля дорівнює нулю.
Якщо комплексне число  відмінне від нуля
відмінне від нуля  , то корінь
, то корінь 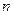 -го степеня
-го степеня  має рівно
має рівно 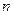 різних значень, що визначаються за другою формулою Муавра:
різних значень, що визначаються за другою формулою Муавра:

 ,
,
де  ;
; 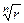 – арифметичне значення кореня з додатного числа.
– арифметичне значення кореня з додатного числа.
На комплексній площині всі корені 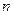 -го степеня
-го степеня  з комплексного числа
з комплексного числа  зображуються вершинами правильного
зображуються вершинами правильного 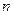 -кутника, вписаного в коло з центром у початку координат і радіусом
-кутника, вписаного в коло з центром у початку координат і радіусом 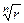 .
.
Приклад 1. Піднести до степеня:  .
.
Розв’язання. Запишемо число  в тригонометричній формі
в тригонометричній формі
 .
.
За першою формулою Муавра



 .
.
Приклад 2. Знайти всі значення кореня:
а)  ; б)
; б)  .
.
Розв’язання.
а) Запишемо підкореневе число  в тригонометричній формі
в тригонометричній формі
 .
.
За другою формулою Муавра


 , де
, де  .
.
При  :
: 
 .
.
При  :
: 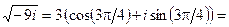
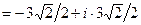 .
.
б) Запишемо підкореневе число  в тригонометричній формі
в тригонометричній формі
 .
.
За другою формулою Муавра

 , де
, де  .
.
 .
.
При  .
.
При  .
.
При 
 .
.
1.6. Многочлени. Розкладання на множники.
Розв’язання квадратних рівнянь
Функція комплексної змінної

називається многочленом 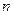 -го степеня стандартного вигляду.
-го степеня стандартного вигляду.
Тут  – комплексний аргумент:
– комплексний аргумент: 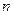 – степінь многочлена;
– степінь многочлена;  – сталі комплексні коефіцієнти;
– сталі комплексні коефіцієнти; 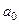 називається старшим коефіцієнтом, причому
називається старшим коефіцієнтом, причому  ;
;  називається вільним членом.
називається вільним членом.
Теорема 1 (теорема Безу). При діленні многочлена  на різницю
на різницю  остача від ділення дорівнює
остача від ділення дорівнює  .
.
Доведення. 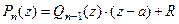 . Нехай
. Нехай  , тоді
, тоді  .
.
Наслідок 1. Якщо  – корінь многочлена
– корінь многочлена  , то цей многочлен
, то цей многочлен  ділиться без остачі на різницю
ділиться без остачі на різницю  , тобто розкладається на множники
, тобто розкладається на множники
 ,
,
де частка  – многочлен на одиницю меншого степеня.
– многочлен на одиницю меншого степеня.
Теорема 2 (основна теорема алгебри). Будь-який многочлен  ненульового степеня
ненульового степеня  має хоча б один корінь (дійсний чи комплексний).
має хоча б один корінь (дійсний чи комплексний).
Наслідок 2. Будь-який многочлен  ненульового степеня
ненульового степеня  має рівно
має рівно 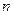 коренів, серед яких можуть бути однакові.
коренів, серед яких можуть бути однакові.
Наслідок 3. Будь-який многочлен  ненульового степеня
ненульового степеня  розкладається на множники у вигляді:
розкладається на множники у вигляді:
 ,
,
де 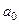 – старший коефіцієнт;
– старший коефіцієнт;  – різні (дійсні чи комплексні) корені;
– різні (дійсні чи комплексні) корені; 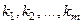 – відповідні кратності цих коренів, причому
– відповідні кратності цих коренів, причому  .
.
Корені квадратного рівняння

з комплексними коефіцієнтами  знаходяться за відомими формулами
знаходяться за відомими формулами
 ,
,
де  – одне зі значень квадратного кореня з дискримінанта
– одне зі значень квадратного кореня з дискримінанта  .
.
На множині комплексних чисел для коренів квадратного рівняння залишається справедливою теорема Вієта:
 ,
,  .
.
Приклад. Розв’язати квадратне рівняння:
а)  ; б)
; б)  ;
;
в)  .
.
Розв’язання.
а)  ;
;  ;
;
 .
.
б)  ;
;

 ;
;  ;
;
 ;
;  .
.
в)  ;
; 

 ;
;
 ;
;
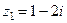 ;
;  .
.
2. Топологія множини комплексних чисел.
Комплексні функції дійсної змінної
2.1. Відстань між точками. Окіл точки.
Нескінченно віддалена точка.
Розширена комплексна площина
Розглядається комплексна площина  .
.
Відстанню  між точками
між точками 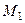 і
і  , що зображають комплексні числа
, що зображають комплексні числа  і
і  , називається довжина відповідного вектора
, називається довжина відповідного вектора  :
:
 ,
,
тобто відстань між комплексними числами  і
і  дорівнює модулю їх різниці
дорівнює модулю їх різниці  .
.
 Нехай
Нехай  – довільне додатне дійсне число
– довільне додатне дійсне число  .
.
Множина точок 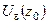 , що задовольняють умову
, що задовольняють умову  , називається
, називається  -околом скінченної точки
-околом скінченної точки  . Окіл точки
. Окіл точки  – це внутрішність круга з центром в цій точці
– це внутрішність круга з центром в цій точці  і радіусом
і радіусом  (
(  -окіл точки
-окіл точки  заштрихований на рис.4).
заштрихований на рис.4).
Для комплексних чисел особливу роль відіграє символ 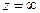 – нескінченно віддалена точка.
– нескінченно віддалена точка.
Зауваження 1. Для невластивого комплексного числа 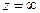 модуль дорівнює
модуль дорівнює  , а поняття аргументу, дійсної та уявної частини позбавлені змісту.
, а поняття аргументу, дійсної та уявної частини позбавлені змісту.
Зауваження 2. Нескінченно віддалена точка 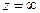 – це зовнішність круга нескінченно великого радіуса з центром у початку координат. Іншими словами, нескінченно віддалена точка
– це зовнішність круга нескінченно великого радіуса з центром у початку координат. Іншими словами, нескінченно віддалена точка 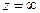 – це об’єднання всіх точок кола нескінченно великого радіуса з центром у початку координат.
– це об’єднання всіх точок кола нескінченно великого радіуса з центром у початку координат.
Вся комплексна площина  , що доповнена нескінченно віддаленою точкою
, що доповнена нескінченно віддаленою точкою 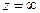 , називається розширеною комплексною площиною
, називається розширеною комплексною площиною  .
.
Зауваження 3. Склеюючи всі точки кола нескінченно великого радіуса з центром у початку координат, отримуємо сферу – ще одне зображення розширеної множини комплексних чисел  . Точка
. Точка 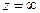 нічим не відрізняється від інших точок: можна розглядати її окіл, перетин ліній в
нічим не відрізняється від інших точок: можна розглядати її окіл, перетин ліній в 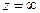 і т.п.
і т.п.
 Нехай
Нехай  – довільне додатне дійсне число
– довільне додатне дійсне число  .
.
Множина точок  , що задовольняють умову
, що задовольняють умову  , називається
, називається  -околом нескінченно віддаленої точки
-околом нескінченно віддаленої точки 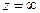 . Окіл точки
. Окіл точки 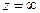 – це зовнішність круга з центром в початку координат і радіусом
– це зовнішність круга з центром в початку координат і радіусом  (
(  -окіл точки
-окіл точки 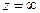 заштрихований на рис.5).
заштрихований на рис.5).
Наочне уявлення про окіл нескінченно віддаленої точки 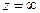 дає стереографічна проекція, що визначає взаємно однозначну відповідність точок розширеної комплексної площини та точок сфери Рімана – сфери одиничного діаметра, що дотикається до площини в початку координат (рис. 6).
дає стереографічна проекція, що визначає взаємно однозначну відповідність точок розширеної комплексної площини та точок сфери Рімана – сфери одиничного діаметра, що дотикається до площини в початку координат (рис. 6).
 Нехай
Нехай  – вертикальний діаметр (
– вертикальний діаметр (  – південний, а
– південний, а  – північний полюс). Для довільної скінченної точки
– північний полюс). Для довільної скінченної точки  комплексної площини точка
комплексної площини точка  перетину відрізка
перетину відрізка  зі сферою називається стереографічною проекцією точки
зі сферою називається стереографічною проекцією точки  .
.
Така відповідність буде взаємно однозначною для всієї розширеної комплексної площини, якщо прийняти, що північний полюс  служить стереографічною проекцією єдиної нескінченно віддаленої точки
служить стереографічною проекцією єдиної нескінченно віддаленої точки 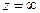 .
.
Зауваження 4. Прямій чи колу на площині при стереографічній проекції відповідає коло на сфері. Зокрема, паралельним прямим відповідають кола, що дотикаються в нескінченно віддаленій точці 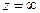 .
.
2.2. Область та її межа
Непорожня множина  комплексної площини чи розширеної комплексної площини називається областю, якщо виконуються такі умови: 1) вона відкрита, тобто разом з кожною своєю точкою містить деякий окіл цієї точки; 2) вона зв’язна, тобто будь-які дві її точки можна сполучити деякою ламаною
комплексної площини чи розширеної комплексної площини називається областю, якщо виконуються такі умови: 1) вона відкрита, тобто разом з кожною своєю точкою містить деякий окіл цієї точки; 2) вона зв’язна, тобто будь-які дві її точки можна сполучити деякою ламаною  , всі точки якої належать цій множині
, всі точки якої належать цій множині  .
.
Зауваження 1. Ламана  може бути необмеженою лінією, що проходить через
може бути необмеженою лінією, що проходить через 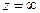 . При цьому вона залишається обмеженою на сфері Рімана.
. При цьому вона залишається обмеженою на сфері Рімана.
Точка  називається межовою точкою області
називається межовою точкою області  , якщо в кожному її околі містяться точки, що належать і що не належать цій області.
, якщо в кожному її околі містяться точки, що належать і що не належать цій області.
Множина всіх межових точок 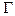 області
області  називається межею цієї області.
називається межею цієї області.
Зауваження 2. Надалі розглядаються області, межа яких 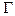 складається зі скінченного числа кусково-гладких кривих та ізольованих точок. Межа може мати дві сторони – два “берега” розрізу.
складається зі скінченного числа кусково-гладких кривих та ізольованих точок. Межа може мати дві сторони – два “берега” розрізу.
Якщо при русі вздовж межі 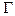 область
область  весь час залишається зліва, то такий напрям орієнтації межі
весь час залишається зліва, то такий напрям орієнтації межі 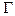 називається додатним обходом.
називається додатним обходом.
Об’єднання області  з її межею
з її межею 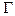 , називається замкненою областю (замиканням області
, називається замкненою областю (замиканням області  ) і позначається
) і позначається  .
.
Якщо межу o6лacті утворює одна лінія, що не має самоперетину, то область називається однозв'язною (рис. 7), а коли межу o6лacті утворюють 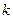 таких л1ній, що не мають самоперетину і спільних точок, то область називається
таких л1ній, що не мають самоперетину і спільних точок, то область називається 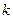 -зв'язною (на рис. 8 зображена тризв’язна область).
-зв'язною (на рис. 8 зображена тризв’язна область).
 |
Зауваження 3. Однозв’язна область  – це область, в якій довільну замкнену криву, що їй належить, можна неперервною деформацією стягнути в точку, залишаючись в цій області
– це область, в якій довільну замкнену криву, що їй належить, можна неперервною деформацією стягнути в точку, залишаючись в цій області  . Однозв’язна область не містить “дірок”, а багатозв’язна область – це область з “дірками”.
. Однозв’язна область не містить “дірок”, а багатозв’язна область – це область з “дірками”.
2.3. Комплексні функції дійсної змінної.
Лінії на комплексній площині
Комплексна функція  дійсної змінної
дійсної змінної 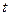 кожному значенню
кожному значенню 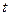 з деякої непорожньої множини
з деякої непорожньої множини  дійсних чисел за певним законом ставить у відповідність одне єдине значення комплексної змінної
дійсних чисел за певним законом ставить у відповідність одне єдине значення комплексної змінної  з деякої області
з деякої області  комплексної площини. Комплексна функція
комплексної площини. Комплексна функція  дійсної змінної
дійсної змінної 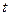 визначається рівністю
визначається рівністю
 ,
,  ,
,
де  та
та 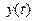 – задані дійсні функції (відповідно дійсна і уявна частини змінної
– задані дійсні функції (відповідно дійсна і уявна частини змінної  ).
).
Зауваження 1. Надалі розглядаються неперервні функції  та
та 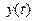 , задані на відрізку
, задані на відрізку  .
.
Функція  ,
,  в комплексно-параметричній формі задає деяку неперервну лінію
в комплексно-параметричній формі задає деяку неперервну лінію  (рис. 9). Параметричні рівняння цієї лінії:
(рис. 9). Параметричні рівняння цієї лінії:  ,
,  ,
,  .
.
 |
Крива називається простою, якщо вона не має точок самоперетину:  , тобто всі точки різні, крім, можливо, початкової
, тобто всі точки різні, крім, можливо, початкової  і кінцевої
і кінцевої  .
.
Крива називається замкненою, якщо її початкова і кінцева точки співпадають:  .
.
Орієнтацію (напрям обходу) замкненої кривої  (контуру) можна задати трьома її точками або двома її точками і однією внутрішньою точкою області
(контуру) можна задати трьома її точками або двома її точками і однією внутрішньою точкою області  , що обмежена даною лінією
, що обмежена даною лінією  .
.
Зауваження 2. Крива на комплексній площині може бути задана в неявній формі рівнянням  .
.
Приклад 1. Визначити вид і зобразити на комплексній площині лінії, задані рівняннями:
а)  ; б)
; б)  ; в)
; в) 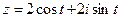 .
.
Розв’язання. Щоб визначити вид лінії, підставимо в її рівняння  і зведемо його до відповідного стандартного вигляду. Потім побудуємо цю лінію.
і зведемо його до відповідного стандартного вигляду. Потім побудуємо цю лінію.
а)  ;
; 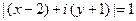 ;
;
 ;
;  – коло
– коло
радіуса  з центром у точці
з центром у точці  (рис.10).
(рис.10).
б)  ;
; 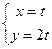 – похила пряма, задана
– похила пряма, задана
в параметричній формі, її явне рівняння  (рис.11).
(рис.11).
в)  ;
;  – коло радіуса
– коло радіуса

 з центром у початку координат, задане в параметричній формі (рис.12).
з центром у початку координат, задане в параметричній формі (рис.12).
Приклад 2. На комплексній площині зобразити замкнену область  , що задана нерівностями:
, що задана нерівностями:
а) 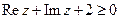 ,
,  ;
;
б) 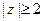 ,
,  .
.
Розв’язання. Якщо замінити знак нерівності на знак рівності, то одержується рівняння лінії – частини межі відповідної області. Кожна лінія розбиває комплексну площину на частини. Вибирається та частина, довільно взята внутрішня пробна точка якої задовольняє відповідну нерівність. Шукана область, задана системою нерівностей, знаходиться як перетин вибраних множин.
а)  ;
;  ,
,  – похила
– похила
пряма;  – коло радіуса
– коло радіуса  з центром у точці
з центром у точці  . Шукана область заштрихована на рис. 13.
. Шукана область заштрихована на рис. 13.
б)  ;
; 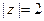 – коло радіуса
– коло радіуса  з центром
з центром
у початку координат;  і
і  – два промені, що виходять з початку координат. Шукана область заштрихована на рис. 14.
– два промені, що виходять з початку координат. Шукана область заштрихована на рис. 14.
 |
2.4. Диференціювання та інтегрування
комплексної функції дійсної змінної
Комплексній змінній  відповідає вектор-функція, тому диференціювання та інтегрування комплексної функції дійсної змінної здійснюється аналогічно відповідним операціям над вектор-функцією дійсного аргументу.
відповідає вектор-функція, тому диференціювання та інтегрування комплексної функції дійсної змінної здійснюється аналогічно відповідним операціям над вектор-функцією дійсного аргументу.
Для знаходження похідної  комплексної функції
комплексної функції  дійсної змінної треба продиференціювати окремо дійсну
дійсної змінної треба продиференціювати окремо дійсну  та уявну
та уявну 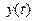 частини:
частини:
 .
.
Зауваження 1. На комплексній площині дотична до кривої  в точці
в точці  задається в комплексно-параметричній формі рівнянням
задається в комплексно-параметричній формі рівнянням 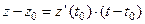 .
.
Приклад 1. Знайти рівняння дотичної до комплексно-параметрично заданої лінії  в точці
в точці  , що відповідає указаному значенню параметра
, що відповідає указаному значенню параметра  :
:
 ,
, 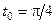 .
.
Розв’язання. 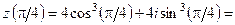
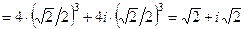 ;
;
 ;
;
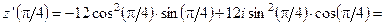
 ;
;
 – дотична.
– дотична.
Для знаходження інтеграла  комплексної функції
комплексної функції  дійсної змінної треба проінтегрувати окремо дійсну
дійсної змінної треба проінтегрувати окремо дійсну  та уявну
та уявну 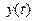 частини:
частини:
 .
.
Приклад 2. Знайти інтеграл:
 .
.
Розв’язання. 
 .
.
3. Функції комплексної змінної. Похідна.
Поняття аналітичної функції. Конформне відображення
3.1. Поняття функції комплексної змінної.
Границя та неперервність
Для геометричного тлумачення поняття функції комплексної змінної розглядаються два екземпляри площини комплексних чисел:  -площина
-площина  і
і  -площина
-площина  .
.
Нехай на  -площині задана довільна множина точок
-площині задана довільна множина точок  . Якщо кожній точці
. Якщо кожній точці  множини
множини  за певним законом
за певним законом  поставлено у відповідність одну точку
поставлено у відповідність одну точку  (або декілька точок)
(або декілька точок)  -площини, то говорять, що на множині
-площини, то говорять, що на множині  задано однозначну (або багатозначну) комплексну функцію комплексної змінної
задано однозначну (або багатозначну) комплексну функцію комплексної змінної 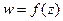 .
.  називається множиною визначення функції
називається множиною визначення функції 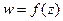 , а множина
, а множина  усіх значень
усіх значень  , що приймає функція, називається множиною значень функції
, що приймає функція, називається множиною значень функції 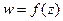 .
.
Зауваження 1. Множина  може бути дуже складної та різноманітної структури. Надалі розглядаються лише випадки, коли множини
може бути дуже складної та різноманітної структури. Надалі розглядаються лише випадки, коли множини  та
та  є областями.
є областями.
Комплексна функція 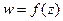 – це відображення області
– це відображення області 
 -площини на область
-площини на область 
 -площини (рис. 15). Якщо функція
-площини (рис. 15). Якщо функція 123456789Следующая ⇒