 |
|
Допоміжні формули Ейлера
 ;
; 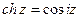 ;
;  ;
; 
дають зв’язок гіперболічних функцій з тригонометричними.
Зауваження 2. Геометрично зв’язок гіперболічних функцій з тригонометричними зводиться до поворотів на  образів і прообразів.
образів і прообразів.
Зауваження 3. При комплексних аргументах зникають принципові відмінності між показниковою, тригонометричними і гіперболічними функціями: експонента  стає періодичною,
стає періодичною,  і
і  – необмеженими і т.п. Формули Ейлера відображають тісний внутрішній зв’язок цих функцій: їх можна розглядати як різні прояви одних і тих же закономірностей.
– необмеженими і т.п. Формули Ейлера відображають тісний внутрішній зв’язок цих функцій: їх можна розглядати як різні прояви одних і тих же закономірностей.
Приклад 1. Знайти  .
.
Розв’язання. 


 .
.
4.5. Логарифмічна функція
Логарифмічна функція комплексної змінної визначається як обернена до показникової:
Комплексне число  називається натуральним логарифмом ненульового комплексного числа
називається натуральним логарифмом ненульового комплексного числа  , якщо виконується рівність
, якщо виконується рівність 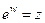 .
.
Нехай  ;
;  . Тоді за означенням
. Тоді за означенням
 ;
;  ;
;
 ;
;  ,
,  .
.
Звідси 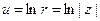 – звичайний натуральний логарифм додатного числа
– звичайний натуральний логарифм додатного числа  ;
;  – вся множина значень аргументу ненульового комплексного числа
– вся множина значень аргументу ненульового комплексного числа  .
.
Отже,
 .
.
Останній вираз показує, що функція  є нескінченнозначною і визначена на всій комплексній площині, за винятком початку координат
є нескінченнозначною і визначена на всій комплексній площині, за винятком початку координат  .
.
Нехай в деякій області  вибором одного зі значень багатозначної функції
вибором одного зі значень багатозначної функції  одержана деяка однозначна функція
одержана деяка однозначна функція 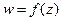 . Якщо ця функція
. Якщо ця функція 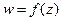 неперервна в області
неперервна в області  , то вона називається однозначною гілкою багатозначної функції
, то вона називається однозначною гілкою багатозначної функції  .
.
Зауваження 1. Багатозначну функцію  можна розглядати як однозначну, але не на комплексній площині, а на деякому більш складному геометричному об’єкті – Римановій поверхні, що утворюється шляхом “склеювання” певним чином між собою відповідної (скінченної чи нескінченної) кількості екземплярів комплексної площини. Наприклад, кореневу функцію
можна розглядати як однозначну, але не на комплексній площині, а на деякому більш складному геометричному об’єкті – Римановій поверхні, що утворюється шляхом “склеювання” певним чином між собою відповідної (скінченної чи нескінченної) кількості екземплярів комплексної площини. Наприклад, кореневу функцію  можна розглядати як однозначну, множиною визначення якої служить трилиста поверхня (“склеєна” з трьох екземплярів площини), а множиною значень є дволиста поверхня (“склеєна” з двох екземплярів площини).
можна розглядати як однозначну, множиною визначення якої служить трилиста поверхня (“склеєна” з трьох екземплярів площини), а множиною значень є дволиста поверхня (“склеєна” з двох екземплярів площини).
Однозначну гілку логарифмічної функції  можна отримати в будь-якій частині комплексної площини, що не містить початку координат, шляхом виділення відповідного проміжку змінювання його уявної частини.
можна отримати в будь-якій частині комплексної площини, що не містить початку координат, шляхом виділення відповідного проміжку змінювання його уявної частини.
Якщо для аргументу  обмежитися його головним значенням
обмежитися його головним значенням  , то одержимо однозначну гілку
, то одержимо однозначну гілку
 ,
,
що називається головним значенням логарифму.
Зауваження 2. Якщо число  – дійсне додатне, тоді головне значення аргументу
– дійсне додатне, тоді головне значення аргументу 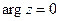 і головне значення логарифму співпадає зі звичайним натуральним логарифмом
і головне значення логарифму співпадає зі звичайним натуральним логарифмом  .
.
Зауваження 3. На логарифм комплексної змінної поширюються основні властивості звичайного логарифму дійсного аргументу:
 ;
;  ;
;
 .
.
Область  , що відповідає однозначній гілці логарифму, не може включати точку
, що відповідає однозначній гілці логарифму, не може включати точку  як внутрішню. Точку
як внутрішню. Точку  не можна обійти, залишаючись у цій області, оскільки при кожному обході в заданому напрямі аргумент
не можна обійти, залишаючись у цій області, оскільки при кожному обході в заданому напрямі аргумент  одержує приріст
одержує приріст 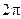 чи
чи  і відбувається перехід до нового значення логарифму
і відбувається перехід до нового значення логарифму  . Тому
. Тому  є так званою точкою розгалуження багатозначного логарифму
є так званою точкою розгалуження багатозначного логарифму  .
.
Зауваження 4. Точкою розгалуження логарифмічної функції є також 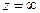 .
.
Зауваження 5. За допомогою логарифмічної функції визначаються:
а) загальна степенева функція  , де показник
, де показник  – довільне комплексне число. Ця функція багатозначна, її головне значення
– довільне комплексне число. Ця функція багатозначна, її головне значення  .
.
б) загальна показникова функція  , де основа
, де основа  – довільне ненульове комплексне число. Ця функція багатозначна, її головне значення
– довільне ненульове комплексне число. Ця функція багатозначна, її головне значення  .
.
в) показниково-степенева функція  , де основа відмінна від нуля
, де основа відмінна від нуля  . Ця функція нескінченнозначна, її головне значення
. Ця функція нескінченнозначна, її головне значення  .
.
Зауваження 6. Багатозначні обернені тригонометричні і обернені гіперболічні функції визначаються як розв’язки відповідних рівнянь для прямих функцій. Переходячи в цих рівняннях за формулами Ейлера до експоненти, вказані аркфункції також можна виразити через логарифмічну функцію. Наприклад:
 ;
;  ;
;
 ;
;  .
.
Приклад 1. Знайти 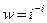 .
.
Розв’язання. 
 ;
;  .
.
Приклад 2. Розв’язати рівняння 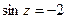 .
.
Розв’язання. 



 ;
;  .
.
5. Інтеграл функції комплексної змінної
5.1. Поняття комплексного інтеграла
Нехай функція  неперервна та однозначна в деякій області
неперервна та однозначна в деякій області  , а
, а  – будь-яка кусково-гладка крива в цій області (рис. 22). Розіб’ємо цю криву довільним чином на
– будь-яка кусково-гладка крива в цій області (рис. 22). Розіб’ємо цю криву довільним чином на 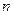 елементарних дуг
елементарних дуг  точками
точками  у напрямку від точки
у напрямку від точки  до точки
до точки  . Кожній елементарній дузі
. Кожній елементарній дузі  відповідає елементарна хорда
відповідає елементарна хорда  . На кожній елементарній дузі
. На кожній елементарній дузі  виберемо довільну точку
виберемо довільну точку  і складемо інтегральну суму
і складемо інтегральну суму  для функції
для функції  на кривій
на кривій  .
.
 |
Границя інтегральної суми при необмеженому здрібненні розбиття (незалежно від способу розбиття та вибору точок) називається інтегралом (контурним інтегралом) комплексної функції
 по кривій (контуру)
по кривій (контуру)  :
:
 ,
,
де  – диференціал комплексного аргументу.
– диференціал комплексного аргументу.
Інтеграл від комплексної функції можна виразити через два дійсні криволінійні інтеграли за координатами:
 .
.
Тому для інтеграла від комплексної функції справедливі відповідні властивості криволінійних інтегралів. Зокрема, при зміні напряму обходу кривої цей інтеграл тільки змінює знак:
 .
.
Як і для дійсних криволінійних інтегралів, обчислення інтеграла від комплексної функції зводиться за допомогою методу заміни змінної до обчислення звичайного визначеного інтеграла.
Приклад. Обчислити заданий інтеграл по вказаній дузі:
а)  ;
;  – коло.
– коло.
б)  ;
; 
– дуга параболи.
Розв’язання. а) 
 .
.
б) 



 .
.
Зауваження. Для існування інтеграла досить неперервності підінтегральної функції 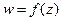 , тому інтеграл може існувати і у випадку неаналітичності цієї функції.
, тому інтеграл може існувати і у випадку неаналітичності цієї функції.