Главная | Обратная связь

Основні поняття про ряди з комплексними членами

Теорема 1. Числовий ряд з комплексними членами , де збігається тоді і тільки тоді, коли збігаються обидва ряди і , складені з дійсних і уявних частин.

Ряд називається абсолютно збіжним, якщо збігається ряд з модулів його членів . Ряд називається умовно збіжним, якщо сам ряд збігається, а ряд з модулів його членів розбігається.

Зауваження. Дослідження на збіжність рядів з комплексними членами зводиться до дослідження рядів з дійсними членами, що здійснюється за відомими ознаками збіжності дійсних рядів.

Приклад 1. Дослідити на збіжність:

а) ; б) ;

в) ; г) .

Розв’язання.

а) Обидва дійсні ряди і збігаються – перший за ознакою Даламбера, а другий за радикальною ознакою Коші (покажіть це самостійно). Тому заданий ряд та­кож збігається.

б) Ряд з дійсних частин розбігається як гармонічний, тому заданий ряд теж розбігається (хоча ряд з уяв­них частин збігається за ознакою Даламбера).

в) Ряд з дійсних частин збігається як узагальнений гармонічний з показником степеня , а ряд з уяв­них частин розбігається як геометрична прогресія зі знаменником 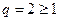. Тому заданий ряд теж роз­бі­гається.

г) Обидва дійсні ряди 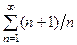і розбігаються, оскільки не задовольняють необхідну ознаку збіжності (по­ка­жіть це самостійно). Тому заданий ряд також розбігається.

Приклад 2. Показати, що заданий ряд збігається абсолютно

.

Розв’язання. Дослідимо на збіжність ряд із модулів:

.

Цей ряд збігається як геометрична прогресія зі знаменником . Тому заданий ряд збігається абсолютно.

Нехай в деякій області комплексної площини задана послідовність функцій комплексної змінної , , , , . Вираз (нескінченна сума)

називається функціональним рядом з комплексними членами.

Функціональний ряд називається збіжним у точ­ці , якщо збігається відповідний числовий ряд .

Мно­жина всіх точок збіжності називається областю збіж­ності.

Теорема 2 (теорема Вейерштрасса). Якщо члени функціональ­ного ряду неперервні в області і ряд збігається рівномірно, то сума ряду 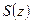– неперервна в і допускає почленне інтегруван­ня вздовж довільної кривої , що лежить в області :

.

Теорема 3. Якщо члени функціонального ряду аналітичні в області і ряд збігається рівномірно в будь-якій замкненій області, що належить , то сума ряду 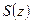– аналітична в області і допускає почленне диференціювання довільне число разів:

; .