Главная | Обратная связь

Завдання на самост. розрах. роботу.

Елементи обчислювальної геометрії.

До задач обчислювальної геометрії що застосовуються в ГІС відносять аналіз близькості та зонування території

 

Аналіз близькості –цепошук об'єктів, що лежать на визначеній відстані від початкового об'єкта або знаходження найближчих об’єктів до объекту – джерела.

 

1) Класична задача про поштові відділення є однією з перших задач обчислювальної геометрії.

В місті є поштових відділень. Людина, знаходячись у певному місці, запитує про найближче поштове відділення. (Сучасним прикладом буде підключення користувача до найближчого вузла мережі мобільних телефонів).

2) Є план міста з нанесеними на нього місцями розміщення пожежних частин. Знайти найближчу до кожного дому пожежну частину.

 

Зонування території – встановлення області обслуговування (інш. сл. поділ на сфери впливу)

Наприклад,

1) розподіл зон обслуговування мережі вулиць до найближчих технічних эксплуатаційних баз міста.

2) визначення ареалів поширення даних спостережень мережі метеорологічних станцій, нерівномірно розміщеній у межах розглянутої території.

 

Математично подібні задачі формулюються так.

На площині задано множину з точок «центрів». Потрібно для кожної точки визначити область таку, що для будь-якої точки -ї області відстань до була менша ніж до будь-якої іншої з множини .

Такі задачі розв’язуються шляхом розбиття території на полігони Тіссена – Вороного.

 

Полігони Вороного розділяють територію на області близькості до заданих точок.

 

Діаграма Вороного.

Діаграма Вороного (полігони Тіссена) для системи точок – це многокутник, утворений відрізками перпендикулярів, проведених до середин сторін, що сполучають дві найближчих сусідніх точки.

 

Наприклад для двох точок–«центрів»,області найближчих точок буде розділяти пряма відстань від якої до «центрів» буде однакова. Очевидно, що пряма буде проходити через середину відрізка і до нього. (Рис). Для 3-х центрів отримаємо вже 1-ну точку перетину.Для більшої кількості точок отримаємо щось схоже на (нерегулярну) стільникову структуру.

 

Всі ми дивуємося коли дивимось на рамку з сотами як бджоли їх ліплять з такою точністю.

Все стає зрозуміло оскільки в основі ідеї діаграми лежить простий природній принцип – якщо декілька точок одночасно і з однаковою швидкістю почнуть збільшувати свої розміри, наприклад рости клітини то (на площині) спочатку це будуть круги, а потім по мірі стиковки утворюються многокутники.

 

Інтересним є факт що подібні ідеї зараз вже використовують у таких практичних задачах як оптимальне перепланування квартири. Оскільки Діаграма Вороного дозволяє створити співрозмірну структуру нових перегородок, зручнішу попередню наявністю плавніших контурів та відсутністю явних невикористовуваних прохідних площ.

Крім того диаграмма Вороного позволяет создавать максимально крепкие структуры с использованием минимального количества материала. Тому метод этот часто используется в инженерных справах

 

Діаграму Вороного будувати просто, якщо перед цим була виконана тріангуляція Делоне.

(нагадаємо означення)

Тріангуляція –мережа трикутників, утворена на множині точок (вузлів) шляхом з’єднання їх відрізками, які не перетинаються. Зрозуміло, що способів тр-ції може бути багато.

Тріангуляція Делоне –всі трикутники мережі прагнуть до правильної форми. В основі тріангуляції Делоне лежить круговий критерій: якщо провести коло через довільні три точки, то інші точки не повинні попадати в нього.

 

Кожна область Вороного будується з'єднанням серединних перпендикулярів у вихідних трикутниках тріангуляції. В цьому розумінні діаграма Вороного і тріангуляція Делоне є взаємно двоїстими. Рис.

Таким чином кожна вершина многокутника є перетином серединних перпендикулярів трикутника тобто є центром описаного кола. Це є внутрішні вершини діаграми Вороного. Зовнішні вершини діаграми Вороного (ті, що лежать на границі області) утворені перетином серединних перпендикулярів із границею області.

 

Визначення сторін діаграми Вороного.

Для визначення сторін діаграми Вороного використовується той факт, що кожна сторона діаграми є серединним перпендикуляром до однієї із сторін тріангуляції Делоне.

Тобто для двох точок тріангуляції , 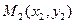маємо рівняння прямої що проходить через середину відрізка з вектором нормалі .

Координати середини відрізка будуть , а к-ти вектора нормалі . Отже рівняння сторони діаграми що проходить між точками та буде ,

або розписавши

 

Значення координат внутрішніх вершин полігона (діаграми) знаходимо як координати точок перетину серединних перпендикулярів. Наприклад для 3-х точок тріангуляції , , 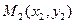отримаємо систему рівнянь

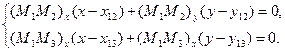
Тут , – координати вектора , а , – к-ти середини відрізка .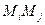

Приклад.

Задано точки тріангуляції , , .

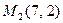1) Знаходимо середини відрізків ,

2) Знаходимо к-ти векторів ,

3) Розв’язуємо систему рівнянь

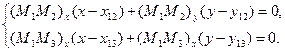
Тобто внутрішня вершина діаграми що відповідає точкам , , 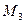буде .

Зауважимо що через точку буде проходити і третя сторона діаграми (Рис.)

.

 

Для визначення координат зовнішніх вершин використовується рівняння сторони діаграми яка перетинає межу області та рівняння самої межі. Наприклад для прямокутної області з сторонами | | осям к-т межа буде визначатися рівняннями , , , . Тоді система рівнянь для визначення координати вершини на перетині сторони діаграми між точками та та межею буде

звідки легко шукається значення

По аналогії легко знайти координати вершини на перетині сторони діаграми, що проходить наприклад, між точками та 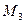з межею

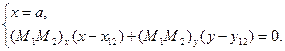
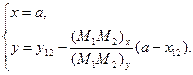
Так з попереднього прикладу, точки перетину сторін діаграми з осями координат будуть

З віссю :

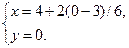
З віссю :

Крім того слід пам’ятати про існування кутових точок області, що утворені перетином межових ліній.

Якщо наприклад всі точки тріангуляції , , 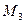попадають в середину квадрата 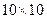, то зовнішніми вершинами діаграми ще будуть точки (0, 0), (10, 0), (10, 10), (0, 10).

Обчислення площі полігонів

 

Площу полігонів обчислюють за формулою

 

При цьому слід пам’ятати, що

.

 

Структуру формули розглянемо

на прикладі п’ятикутника

A1(x1,y1); A2(x2,y2); A3(x3,y3); A4 x4,y4; A5(x5,y5)

 

Многокутник можна розбити на трапеції з послідовними вершинами, площа кожної з яких буде .

причому, якщо то , а якщо то . Тоді очевидно, що сума таких площ 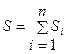буде рівна площі многокутника, яку отримаємо із знаком «+» якщо вершини нумерувати за годинниковою стрілкою та із знаком «–» якщо вершини нумерувати у протилежному напрямку. Отже у будь-якому випадку

Зауваження. Формула справедлива якщо не міняють знак (усі , або усі ) інакше площа многокутника нижче осі буде відніматися від площі, що вище . Якщо ця умова не виконується, то до усіх слід додати одне й те ж саме число, наприклад модуль найменшої з від’ємних ординат .

Приклад.

Обчислимо площу отриманого чотирикутника з діаграми Вороного з вершинами

, , , .

Формулу обчислення площі найзручніше було б запрограмувати на комп’ютері, однак якщо обчислення проводяться вручну, то результати доцільно заносити у таблицю

Таблиця 1. Полігон 1

№ вершини					Сума
	0	0	5	3
	0	6	6	0
			-2
			-12		2S = 48

 

Отже площа чотирикутника буде одиниці.

Зауважимо що тут легко зробити перевірку оскільки маємо трапецію .

 

Завдання на самост. розрах. роботу.

Виконати графічну побудову тріангуляції Делоне і діаграми Вороного для заданої системи 3-х точок у заданому квадраті. Визначити сторони діаграми (записати їх рівняння). Визначити координати вершин діаграми (внутрішні та зовнішні). Обчислити площу кожного з 3-х полігонів та їх сумарну площу.