 |
|
Комплект экзаменационных материалов
Контрольно измерительные материалы
по дисциплине математика
По специальности 44.02.05. Коррекционная педагогика в начальном образовании
\
Тула 2014
Контрольно-измерительные материалы по учебной дисциплине «Математика» разработаны в соответствии с требованиями ФГОС СПО по специальности 44.02.05. Коррекционная педагогика в начальном образовании
Организация-разработчик:
государственное образовательное учреждение среднего профессионального образования Тульской области «Тульский педагогический колледж № 1»
Разработчик: Загурская Наталья Станиславовна, преподаватель математических дисциплин.
Рассмотрено: на ПЦК математики, информатики, естественнонаучных дисциплин, протокол № 1 от 26.08.2014
Рекомендован методическим советом, протокол №3 от 20.11.2014
Паспорт КИМ
Область применения
Комплект контрольно-измерительных материалов предназначен для проверки результатов освоения учебной дисциплиныматематикапрограммы подготовки специалистов среднего звена (ППССЗ) по специальности СПО 44.02.05. Коррекционная педагогика в начальном образовании
1.2. Комплект контрольно-измерительных материалов позволяет оценивать умения и знания по дисциплине математика.
В результате изучения дисциплины студент должен
| Уметь: | |
| У 1 | применять математические методы для решения профессиональных задач |
| У 2 | решать текстовые задачи |
| У 3 | выполнять приближенные вычисления |
| У 4 | проводить элементарную статистическую обработку информации и результатов исследований, представлять полученные данные графически |
| Знать: | |
| З 1 | понятие множества, отношения между множествами, операции над ними |
| З 2 | понятия величины и ее измерения |
| З 3 | историю создания систем единиц величины |
| З 4 | этапы развития понятий натурального числа и нуля |
| З 5 | системы счисления |
| З 6 | понятие текстовой задачи и процесса ее решения |
| З 7 | историю развития геометрии |
| З 8 | основные свойства геометрических фигур на плоскости и в пространстве |
| З 9 | правила приближенных вычислений |
| З 10 | методы математической статистики |
Оценка освоения дисциплины
Основной целью оценки теоретического курса учебной дисциплины является оценка умений и знаний.
Оценка теоретического курса учебной дисциплины осуществляется с использованием следующих форм и методов контроля: устный опрос, тестовые задания, контрольная работа, защита практических заданий.
Типовые задания для экзамена.
Задание 1.
Проверяемые умения и знания: У 1 – У 4, З 1 – З 10.
Текст задания:
А) Тестовое задание.
1.Длина экватора Земли 40000км, а длина экватора на школьном глобусе 1м. Сколько километров земного экватора в 1см глобуса?
A.40 км.
B.400 км;
C.4000000 км.
D.39990 км.
2.На сколько классов разбито множество А множествами В, С и Д (Рис.1.)?
Рис. 1.
A. 
6.
B.4.
C.3.
D.Бесконечно много.
3.Записать множество Х, которое заштриховано на рисунке, с помощью операций пересечения, объединения и разности множеств (Рис.2.).
Рис. 2.
4.Какое из высказываний истинно?
A.3 ≥ 7.
B.Существуют параллелограммы, которые являются прямоугольниками.
C.Число 27 чётное и делится на 3.
D.Любое натуральное число является решением уравнения х+3=7.
5.Записать в десятичной системе счисления число 322, выраженное в пятеричной системе счисления.
A.387.
B.78.
C.87.
D.322.
6. Решите задачу: «Велосипедист был в пути 3ч, причём каждый следующий час он проезжал расстояние вдвое меньшее, чем за предыдущее. Какое расстояние проехал велосипедист за последний час, если весь путь составил 49км?».
A.7 км.
B.14 км.
C.28 км.
D.49 км.
7. Из пунктов А и В, расстояние между которыми 180км, навстречу друг другу выехали велосипедист и мотоциклист. Через какое время они встретятся, если скорость велосипедиста 15км\ч, а мотоциклиста – 30км\ч?
Какое выражение является решением этой задачи?
A.180:15+180:30.
B.180: (15+30).
C.180:15-180:30.
D.180: (30-15).
8. Решите задачу: «В три школы привезли учебники. В первую школу привезли 
всех учебников, во вторую школу - 
оставшихся учебников, а в третью школу - 90 учебников. Сколько всего учебников привезли в школы?».
A.270 учебников.
B.180 учебников.
C.405 учебников.
D.225 учебников.
9.Какое понятие в данном определении является родовым?
Интегралом от a до b функции f называется приращение первообразной F этой функции, то есть F(a)-F(b).
A.Интеграл.
B.Функция f.
C.ПервообразнаяF.
D.Приращение.
10. Какое отношение логического следования составлено неверно?
A.Если число делится на 12, то оно делится на 15.
B.Если число делится на 9, то оно делится на 3.
C.Если молодой человек является студентом ТПК №1, то он является членом студенческого сообщества РФ.
D.Если геометрическая фигура является ромбом, то она является параллелограммом.
11. Какое предложение составлено верно?
A.Для того чтобы число делились на 2, необходимо, чтобы оно делилось на 4.
B.Для того чтобы число делились на 10, необходимо, чтобы оно делилось на 4.
C.Для того чтобы человек мог быть избран президентом РФ, необходимо, чтобы он был гражданином РФ.
D.Для того чтобы геометрическая фигура была ромбом, необходимо, чтобы она являлась квадратом.
12.Какое из высказываний содержит квантор общности?
A.Некоторые дети любят кататься на велосипеде.
B.Все студенты не прогуливают лекции?
C.Каждый прямоугольник является параллелограммом.
D.Все на борьбу с безграмотностью!
13.Отрицанием какого высказывания является следующее предложение?
Все студенты учатся на отлично.
A.Все студенты не учатся на отлично.
B.Каждый студент учится на отлично.
C.Неверно, что все студенты не учатся на отлично.
D.Существуют студенты, которые не учатся на отлично.
14.Найдите пересечение множеств А и В, если А= {2, 7, 4, 9, 3} и В= {2, 5, 1, 7, 9, 3, 6}.
A.А∩В= {2,7,4,9,3}.
B.А∩В= {2,5,1,7,9,3,6}.
C.А∩В= {2,7,9,3}.
D.А∩В= {2,5,1,7,9,3,6,4}.
15. Найдите объединение множеств А и В, если А: {х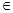 
R, х>5} и В= {х 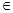R, х≤7}.
A.АUВ=(5; 7].
B.АUВ = (7;+∞);
C.АUВ = (-∞; 5) U (5; +∞).
D.АUВ = [5; +∞).
16. Найдите дополнение множества А до множества В, если А - «множество чисел, кратных 6» и В – «множество чисел, кратных 3».
A.А\В – «множество чисел, кратных 6, но не кратных 3».
B.В\А - «множество чисел, кратных 3, но не кратных 6».
C.А\В - «множество чисел, кратных 6».
D.В\А - «множество чисел, кратных 3».
17. Найдите декартово произведение множеств А и В, если А= {2, 7, 4} и В= {2, 5, 1}.
A.А ×В= {2, 7, 4, 5, 1}.
B.А×В= {2, 7, 4}.
C.А×В= {(2; 2), (2; 5), (2; 1)}.
D.А×В= {(2; 2), (2; 5), (2; 1), (7; 2), (7; 5), (7; 1), (4; 2), (4; 5), (4; 1)}.
18.Иллюстрацией какого декартового произведения является данный рисунок?
A. А= {1, 3}; В= {2, 3}.
B. А= {2, 3}; В= {1, 3}.
C. А= [2, 3]; В= [1, 3].
D. А= [1, 3]; В= [2, 3].
19.Множество А - «геометрических фигур» разбито на классы с помощью подмножеств В - «треугольников», С - «ромбов», Д - «квадратов». Какой класс, из указанных в ответах, может быть в этом разбиении?
- Множество геометрических фигур.
- Множество ромбов.
- Множество квадратов.
- Множество прямоугольников, не являющихся квадратами.
20.Какой способ решения этой задачи неверный: «С двух станций, расстояние между которыми равно 60 км, одновременно в противоположных направлениях выехали два поезда. Первый поезд ехал со скоростью 70 км\ч. С какой скоростью ехал второй поезд, если через 4 часа после выезда расстояние между ними стало равно 700 км?»?
A.(700 - 60):4-70
B.(700 – (70·4+60)):4
C.((700 – 60)-70·4):4
D.((700 – 70)-60·4):4
Б) Тестовое задание
1. Предельная абсолютная погрешность разности приближенных чисел равна:
А) разности предельных абсолютных погрешностей уменьшаемого и вычитаемого;
Б) разности предельных относительных погрешностей уменьшаемого и вычитаемого;
В) сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого;
Г) сумме предельных относительных погрешностей уменьшаемого и вычитаемого.
2. Предельная относительная погрешность частного приближенных чисел равна:
А) сумме предельных относительных погрешностей делимого и делителя;
Б) разности предельных относительных погрешностей делимого и делителя;
В) произведению предельных относительных погрешностей делимого и делителя;
Г) частному предельных относительных погрешностей делимого и делителя.
3. Предельная абсолютная погрешность числа 13,4 <x< 13,6 равна
А) 0,2;
Б) 0,1;
В) 0,05;
Г) 0,74.
4. Предельная относительная погрешность числа 9,18 ± 0,04 равна
А) 0,43;
Б) 0,44;
В) 0,04;
Г) 0,05.
5. На опытной делянке измерили рост пяти саженцев в сантиметрах: 122, 120, 156, 148, 124. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
А) 22;
Б) 10;
В) 12;
Г) 20.
6. Размах выборки 12,1; 12,4; 12,5; 12,4; 12,1; 12,4 равен
А) 0,2;
Б) 6;
В) 12,4;
Г) 0,4.
7. Ветеринар взвесил поросят. Их масса в килограммах такова: 82, 88, 96, 94, 95, 90, 88, 84, 99, 87. Мода и медиана этого набора чисел равны
А) 88 и 99;
Б) 88 и 95;
В) 88 и 88;
Г) 88 и 90.
8. Для службы на подводной лодке отбирают призывников ростом не более 165см. Есть 4 группы призывников, про которые известно следующее:
А) в первой группе средний рост равен 162см;
Б) во второй группе максимальный рост равен 169см;
В) в третьей группе минимальный рост равен 158см;
Г) в четвертой группе медиана ряда роста равна 163см.
В какой из групп половина призывников заведомо годна к службе на подводной лодке?
9. Ломаная линия, вершинами которой являются точки (хi; yi), определяемые элементами статистического ряда, называется
А) диаграммой частот;
Б) гистограммой частот;
В) медианой частот;
Г) полигоном частот.
10. Варианта выборки, делящая вариационный ряд на две части, равные по числу вариант, называется
А) модой;
Б) размахом;
В) медианой;
Г) средним арифметическим.
Задание 2.
Проверяемые умения и знания У 1 – У 4, З 1 – З 10.
Текст задания:
А) Тестовое задание.
1.Высота самой большой горы на земле 9000км, а на рисунке в книге она имеет высоту 30см. Сколько километров в 1см изображения?
A.300 км.
B.30 км.
C.8970 км.
D.9 км.
2. На сколько классов разбито множество А множествами В, С, и Д (Рис.1.)?
A. 
4.
B.6.
C.1.
D.3.
Рис.1.
3.Записать множество Х, которое заштриховано на рисунке, с помощью операций пересечения, объединения и разности множеств (Рис.2.).
A.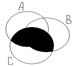 
(А 
В) 
С.
B.(А В) С.
C.(А С) В.
D.(А С) В.
Рис.2.
4.Какое из высказываний истинно?
A.Некоторые ромбы являются трапециями.
B.5 ≥ 5.
C.Число 48,2 натуральное и делится на 2.
D.Всякий треугольник является равносторонним.
5. Записать в десятичной системе счисления число 204, выраженное в шестеричной системе счисления.
A.72.
B.204.
C.612.
D.76.
6. Решите задачу: «Велосипедист был в пути 3ч, причём каждый следующий час он проезжал расстояние вдвое меньшее, чем за предыдущий час. Какое расстояние проехал велосипедист за последний час, если весь путь составил 56км?».
A.8 км.
B.16 км.
C.32 км.
D.56 км.
7. Из пунктов А и В, расстояние между которыми 60км, выехали в противоположных направлениях друг от друга велосипедист и мотоциклист. Какое расстояние будет между ними через 2 часа пути, если скорость велосипедиста 15км\ч, а мотоциклиста – 30км\ч?
Какое выражение является решением этой задачи?
A.60+(30-15)*2.
B.60-(30+15)*2.
C.60+(30+15):2.
D.60+(30+15)*2.
8. Решите задачу: «За три дня туристы проехали 100км. В первый день они проехали 
всего пути, во второй день - 
оставшегося пути. Сколько километров проехали туристы в третий день?».
A.20 км.
B.80 км.
C.50 км.
D.30 км.
9. Какое понятие в данном определении является видовым?
Уравнения, в которых переменная содержится под знаком корня, называются иррациональными уравнениями.
A.Уравнение.
B.Иррациональное уравнение.
C.Переменная.
D.Знак корня.
10.Какое отношение логического следования составлено верно?
A.Если число делится на 12, то оно делится на 15.
B.Если число делится на 3, то оно делится на 30.
C.Если молодой человек является студентом ТПК №1, то он является членом студенческого сообщества РФ.
D.Если геометрическая фигура является параллелограммом, то она является ромбом.
11. Какое предложение составлено не верно?
A.Для того чтобы число делились на 2, необходимо, чтобы оно делилось на 4.
B.Для того чтобы число делились на 30, необходимо, чтобы оно делилось на 15.
C.Для того чтобы человек мог быть избран президентом РФ, необходимо, чтобы он был гражданином РФ.
D.Для того чтобы геометрическая фигура была параллелограммом, достаточно, чтобы она являлась ромбом.
12.Какое из высказываний содержит квантор существования?
A.Некоторые дети любят кататься на велосипеде.
B.Существуют студенты, не прогуливающие лекции?
C.Каждый прямоугольник является параллелограммом.
D.Все на борьбу с безграмотностью!
13.Отрицанием какого высказывания является следующее предложение?
Некоторые дети не хотят учить уроки.
A.Существуют дети, которые хотят учить уроки.
B.Существуют дети, которые не хотят учить уроки.
C.Все дети не хотят учить уроки.
D.Все дети хотят учить уроки.
14. Найдите пересечение множеств А и В, если А: {х 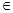R, х≥8} и В= {х 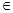R, х≤17}.
A.А∩В = [8; 17].
B.А∩В = [8;+∞).
C.А∩В=(-∞; 8] U (17; +∞).
D.А∩В = (-∞; 7].
15. Найдите объединение множеств А и В, если А= {8, 5, 7, 3} и В= {2, 5, 1, 7, 9, 3, 6}.
A.АUВ= {8, 7, 5, 3}.
B.АUВ = {2, 5, 1, 7, 9, 3, 6}.
C.АUВ= {8, 5, 7, 3, 2, 1, 9, 6}.
D.АUВ= {2, 5, 1, 7, 9, 3, 6, 4}.
16.Найдите дополнение множества А до множества В, если А - « множество тетраэдров», В – «множество пирамид».
A.В\А - «множество тетраэдров».
B.А\В - «множество пирамид».
C.В\А - «множество пирамид, не являющихся тетраэдрами ».
D.А\В- «множество тетраэдров, не являющихся пирамидами».
17. Найдите декартово произведение множеств А и В, если А={а, б} и В={а, б}.
A.А ×В={а; б}.
B.А ×В = {(а; б), (б; а)}.
C.А ×В= {(а; а), (а; б), (б; а), (б; б)}.
D.А ×В= {(а; а), (б; б)}.
18. Декартово произведение каких множеств задано?
A. 
А= {2, 3, 5}; В= {2, 4}.
B.А= {2, 3, 5}; В= [2, 4].
C.А= [2, 5]; В= [2, 4].
D.А= [2, 5]; В= {2, 4}.
19.Множество N-«натуральных чисел» разбито на классы с помощью подмножеств А- «множество чисел, кратных 9» и В- «множество чисел, кратных 7». Какой класс, из предложенных в ответах, может быть в этом разбиении?
A.Множество чисел, кратных 9.
B.Множество чисел, кратных 7.
C.Множество чисел, кратных 7 и 9.
D.Множество натуральных чисел, некратных 9.
20. Какой способ решения этой задачи верный: «Из пунктов А и В одновременно навстречу друг другу выехали велосипедист и мотоциклист. Скорость велосипедиста 15 км\ч, скорость мотоциклиста 25 км\ч. Какое расстояние будет между ними через 3 часа движения, если расстояние между пунктами А и В равно 200км?»?
A.200-(15+25)*3.
B.200-15*3+25*3.
C.200+15*3-25*3.
D.200-(25-15)*3.
Б) Тестовое задание.
1. Предельная абсолютная погрешность разности приближенных чисел равна:
А) разности предельных абсолютных погрешностей уменьшаемого и вычитаемого;
Б) разности предельных относительных погрешностей уменьшаемого и вычитаемого;
В) сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого;
Г) сумме предельных относительных погрешностей уменьшаемого и вычитаемого.
2. Предельная относительная погрешность частного приближенных чисел равна:
А) сумме предельных относительных погрешностей делимого и делителя;
Б) разности предельных относительных погрешностей делимого и делителя;
В) произведению предельных относительных погрешностей делимого и делителя;
Г) частному предельных относительных погрешностей делимого и делителя.
3. Предельная абсолютная погрешность числа 13,4 <x< 13,6 равна
А) 0,2;
Б) 0,1;
В) 0,05;
Г) 0,74.
4. Предельная относительная погрешность числа 9,18 ± 0,04 равна
А) 0,43;
Б) 0,44;
В) 0,04;
Г) 0,05.
5. На опытной делянке измерили рост пяти саженцев в сантиметрах: 122, 120, 156, 148, 124. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
А) 22;
Б) 10;
В) 12;
Г) 20.
6. Размах выборки 12,1; 12,4; 12,5; 12,4; 12,1; 12,4 равен
А) 0,2;
Б) 6;
В) 12,4;
Г) 0,4.
7. Ветеринар взвесил поросят. Их масса в килограммах такова: 82, 88, 96, 94, 95, 90, 88, 84, 99, 87. Мода и медиана этого набора чисел равны
А) 88 и 99;
Б) 88 и 95;
В) 88 и 88;
Г) 88 и 90.
8. Для службы на подводной лодке отбирают призывников ростом не более 165см. Есть 4 группы призывников, про которые известно следующее:
А) в первой группе средний рост равен 162см;
Б) во второй группе максимальный рост равен 169см;
В) в третьей группе минимальный рост равен 158см;
Г) в четвертой группе медиана ряда роста равна 163см.
В какой из групп половина призывников заведомо годна к службе на подводной лодке?
9. Ломаная линия, вершинами которой являются точки (хi; yi), определяемые элементами статистического ряда, называется
А) диаграммой частот;
Б) гистограммой частот;
В) медианой частот;
Г) полигоном частот.
10. Варианта выборки, делящая вариационный ряд на две части, равные по числу вариант, называется
А) модой;
Б) размахом;
В) медианой;
Г) средним арифметическим.
Задание 3.
Проверяемые умения и знания У 1 – У 4, З 1 – З 10.
Текст задания:
А) Тестовое задание.
1.Средний рост солдата-гренадёра 180см, а размер оловянного солдатика - 12см. Чему равен размер ступни оловянного солдатика, если у гренадёра её размер равен 45см?
A.4 см.
B.24 см.
C.48 см.
D.3 см.
2. 
На сколько классов разбито множество А множествами В, С, и Д (Рис.1.)?
A.5.
B.3.
C.6.
D.8.
Рис.1
3.Записать множество Х, которое заштриховано на рисунке, с помощью операции пересечения, объединения и разности множеств (Рис.2.).
A.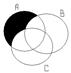 
А\(В С).
B.(А В)\С.
C.А\ (В С).
D.(В С)\А.
Рис.2.
4.Какое из высказываний истинно?
A.5 ≥ 10.
B.Некоторые натуральные числа чётные.
C.Все квадратные уравнения имеют действительные корни.
D.Неравенство 5х-4<0 имеет один корень.
5.Записать в десятичной системе счисления число 333, выраженное в четверичной системе счисление.
A.48.
B.63.
C.444.
D.333.
6. Решите задачу: «Черепаха ползла к реке 4ч, причём каждый следующий час она проползала вдвое меньшее расстояние, чем в предыдущий час. Какое расстояние она проползла за первый час, если всего она преодолела 90м?».
A.6 м.
B.12 м.
C.24 м.
D.48 м.
7. Между пунктами А и В, расстояние 60км. Из пункта А выехал мотоциклист со скоростью 30км\ч. В это же время в том же направлении из пункта В выехал велосипедист со скоростью 15км\ч. Через какое время мотоциклист догонит велосипедиста?
Какое выражение является решением этой задачи?
A.60: (30-15).
B.60: (30+15).
C.60* (30-15).
D.60: 30-60:15.
8.Решите задачу: «В трёх альбомахлежат марки. В первом альбоме - 
всех марок, во втором - 
всех марок, а в третьем альбоме – 80 марок. Сколько всего марок в трёх альбомах?»
A.560 марок.
B.126 марок.
C.360 марок.
D.80 марок.
9. Какое понятие в данном определении является видовым?
Полное линейное пространство со скалярным произведением называется гильбертовым пространством.
A.Скалярное произведение.
B.Пространство.
C.Полное линейное пространство.
D.Гильбертово пространство.
10. Какое отношение логического следования составлено неверно?
A.Если число делится на 14, то оно делится на 7.
B.Если число делится на 25, то оно делится на 5.
C.Если человек является гражданином РФ, то он является президентом РФ.
D.Если геометрическая фигура является квадратом, то она является параллелограммом.
11. Какое предложение составлено неверно?
A.Для того чтобы число делились на 2, необходимо, чтобы оно делилось на 4.
B.Для того чтобы число делились на 15, достаточно, чтобы оно делилось на 30.
C.Для того чтобы человек мог быть избран президентом РФ, необходимо, чтобы он был гражданином РФ.
D.Для того чтобы геометрическая фигура была параллелограммом, достаточно, чтобы она являлась прямоугольником.
12.Какое из высказываний содержит квантор общности?
A.Все дети читали сказки А.С. Пушкина?
B.Все студенты не прогуливают лекции.
C.Существуют прямоугольники, которые не являются параллелограммом.
D.Любой гриб съедобный?
13.Отрицанием какого высказывания является следующее предложение?
Существуют студенты, которые не учатся на отлично.
A.Все студенты не учатся на отлично.
B.Каждый студент учится на отлично.
C.Неверно, что все студенты не учатся на отлично.
D.Существуют студенты, которые учатся на отлично.
14.Найдите пересечение множеств А и В, если А - «множество чисел, кратных 3» и В – «множество чисел, кратных 7».
A.А∩В – «множество чисел, кратных 3 и 7».
B.А∩В – «множество чисел, кратных 3 и не кратных 7».
C.А∩В – «множество чисел, кратных 3 или 7».
D.А∩В – «множество чисел, не кратных 3».
15. Найдите объединение множеств А и В, если А: {х 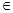R, х>8} и В= {х 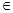R, х≤7}.
A.АUВ = (7; 8].
B.АUВ = (8;+∞).
C.АUВ = (-∞; 7] U (8; +∞).
D.АUВ = (-∞; 7) U [8; +∞).
16. Найдите дополнение множества А до множества В, если А= {2, 7, 4, 9, 3} и
В= {2, 5, 1, 7, 9, 3, 6, 4}.
A.В\А = {2, 7, 4, 9, 3}.
B.А\В= {5, 1, 6}.
C.В\А= {5, 1, 6}.
D.А\В= {2, 5, 1, 7, 9, 3, 6, 4}.
17. Найдите декартово произведение множеств А и В, если А= {2, 7, 4} и В= {8, 5, 1}.
A.А ×В = {2; 7; 4; 8; 5; 1}.
B.А ×В = {(2; 8), (2; 5), (2; 1), (7; 8), (7; 5), (7; 1), (4; 8), (4; 5), (4; 1)}.
C.А ×В= {(2; 8), (2; 5), (2; 1)}.
D.А ×В= {(8; 1), (5; 2), (4; 7)}.
18.Иллюстрацией какого декартового произведения является данный рисунок?
A. 
А= {1, 4}; В= {1, 3}.
B.А= {1, 3}; В= {1, 4}.
C.А= [1, 4]; В= [1, 3].
D.А= [1, 3]; В= [2, 3].
19.Множество А - «геометрических фигур» разбито на классы с помощью подмножеств В - «треугольников», С - «ромбов», Д - «квадратов». Какой класс, из указанных в ответах, не может быть в этом разбиении?
A.Множество геометрических фигур.
B.Множество ромбов, не являющихся квадратами.
C.Множество квадратов.
D.Множество треугольников.
20.Какой способ решения этой задачи неверный: «С двух станций, расстояние между которыми равно 50 км, одновременно в противоположных направлениях выехали два поезда. Второй поезд ехал со скоростью 60 км\ч. С какой скоростью ехал первый поезд, если через 5 часа после выезда расстояние между ними стало равно 500 км?»?
A.(500 - 50):5-60.
B.(500 – (60*5+50)):5.
C.((500 – 50)-60*5):5.
D.((500 – 60)-50*5):5.
Б) Тестовое задание.
1. Предельная абсолютная погрешность разности приближенных чисел равна:
А) разности предельных абсолютных погрешностей уменьшаемого и вычитаемого;
Б) разности предельных относительных погрешностей уменьшаемого и вычитаемого;
В) сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого;
Г) сумме предельных относительных погрешностей уменьшаемого и вычитаемого.
2. Предельная относительная погрешность частного приближенных чисел равна:
А) сумме предельных относительных погрешностей делимого и делителя;
Б) разности предельных относительных погрешностей делимого и делителя;
В) произведению предельных относительных погрешностей делимого и делителя;
Г) частному предельных относительных погрешностей делимого и делителя.
3. Предельная абсолютная погрешность числа 13,4 <x< 13,6 равна
А) 0,2;
Б) 0,1;
В) 0,05;
Г) 0,74.
4. Предельная относительная погрешность числа 9,18 ± 0,04 равна
А) 0,43;
Б) 0,44;
В) 0,04;
Г) 0,05.
5. На опытной делянке измерили рост пяти саженцев в сантиметрах: 122, 120, 156, 148, 124. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
А) 22;
Б) 10;
В) 12;
Г) 20.
6. Размах выборки 12,1; 12,4; 12,5; 12,4; 12,1; 12,4 равен
А) 0,2;
Б) 6;
В) 12,4;
Г) 0,4.
7. Ветеринар взвесил поросят. Их масса в килограммах такова: 82, 88, 96, 94, 95, 90, 88, 84, 99, 87. Мода и медиана этого набора чисел равны
А) 88 и 99;
Б) 88 и 95;
В) 88 и 88;
Г) 88 и 90.
8. Для службы на подводной лодке отбирают призывников ростом не более 165см. Есть 4 группы призывников, про которые известно следующее:
А) в первой группе средний рост равен 162см;
Б) во второй группе максимальный рост равен 169см;
В) в третьей группе минимальный рост равен 158см;
Г) в четвертой группе медиана ряда роста равна 163см.
В какой из групп половина призывников заведомо годна к службе на подводной лодке?
9. Ломаная линия, вершинами которой являются точки (хi; yi), определяемые элементами статистического ряда, называется
А) диаграммой частот;
Б) гистограммой частот;
В) медианой частот;
Г) полигоном частот.
10. Варианта выборки, делящая вариационный ряд на две части, равные по числу вариант, называется
А) модой;
Б) размахом;
В) медианой;
Г) средним арифметическим.
Задание 4.
Проверяемые умения и знания У 1 – У 4, З 1 – З 10.
Текст задания:
А) Тестовое задание.
1.Шоссе, проходящее через Москву, имеет длину 40км, а на карте Москвы его длина 20см. Сколько километров в 1см изображения?
A.2 км.
B.4 км.
C.800 км.
D.100 000 км.
2.На сколько классов разбито множество А множествами В, С и Д (Рис.1.)?
A. 
8.
B.6.
C.4.
D.1.
Рис.1
3.Записать множество Х, которое заштриховано на рисунке, с помощью операций пересечения, объединения и разности множеств (Рис.2.).
A. 
С\(А В).
B.(А В)\С.
C.С\ (А В).
D.(А В)\С.
Рис.2.
4.Какое из высказываний истинно?
A.Число 15 кратно 2 и простое.
B.Число 12 нечётное или кратно 5.
C.Любой корень уравнения обращает его в верное числовое равенство.
D.Существуют треугольники, у которых сумма углов меньше 180º.
5.Запишите в десятичной системе счисления число 202, выраженное в семеричной системе счисления.
A.98.
B.100.
C.49.
D.202.
6.Решите задачу: «Муравей добирался до муравейника 4ч, причём каждый следующий час он проползал расстояние вдвое меньшее, чем за предыдущий час. Какое расстояние муравей прополз за второй час своего путешествия, если весь его путь равен 75м?».
A.20 м.
B.40 м.
C.5 м.
D.10 м.
7. Между пунктами А и В, расстояние 60км. Из пункта А со скоростью 15км\ч выехал велосипедист. В это же время в том же направлении из пункта В выехал мотоциклист со скоростью 30км\ч. Какое расстояние будет между ними через 4 часа пути?
Какое выражение является решением этой задачи?
A.60+(30-15)*4.
B.60-(30-15)*4.
C.60+(30+5)*4.
D.60-(30-15):4.
8. Решите задачу: «В трёх книгах 800 страниц. В первой книге 
всех страниц, во второй книге 
всех страниц. Сколько страниц в третьей книге?».
A.200 страниц.
B.500 страниц.
C.100 страниц.
D.80 страниц.
9. Какое понятие в данном определении является родовым?
Множество, у которого все точки являются внутренними, называется открытым.
A.Множество.
B.Открытое множество.
C.Внутренние точки.
D.Все точки.
10.Какое отношение логического следования составлено верно?
A.Если число делится на 15, то оно делится на 12.
B.Если число делится на 30, то оно делится на 3.
C.Если молодой человек является членом студенческого сообщества РФ, то он является студентом ТПК №1.
D.Если геометрическая фигура является параллелограммом, то она является квадратом.
11. Какое предложение составлено верно?
A.Для того чтобы число делились на 4, достаточно, чтобы оно делилось на 2.
B.Для того чтобы число делились на 10, необходимо, чтобы оно делилось на 100.
C.Для того чтобы быть студентом ТПК №1, достаточно, быть гражданином РФ.
D.Для того чтобы геометрическая фигура была многоугольником, достаточно, чтобы она являлась треугольником.
12.Какое из высказываний содержит квантор существования?
A.Существуют вежливые дети?
B.Некоторые студенты не прогуливают лекции.
C.Каждый прямоугольник является параллелограммом.
D.Все на борьбу с безграмотностью.
13.Отрицанием какого высказывания является следующее предложение?
Некоторые дети любят учить уроки.
A.Существуют дети, которые любят учить уроки.
B.Существуют дети, которые не любят учить уроки.
C.Все дети не любят учить уроки.
D.Все дети любят учить уроки.
14. Найдите пересечение множеств А и В, если А= {8, 5, 7, 3} и В= {2, 5, 1, 7, 9, 3, 6}.
A.А∩В= {7,5,3}.
B.А∩В= {2,5,1,7,9,3,6, 8}.
C.А∩В= {2,7,9,3}.
D.А∩В= {2,5,1,7,9,3,6,4}.
15. Найдите объединение множеств А и В, если А - « множество тетраэдров»,
В – «множество пирамид».
A.АUВ - «множество тетраэдров».
B.АUВ- «множество пирамид».
C.АUВ- «множество пирамид или тетраэдров».
D.АUВ- «множество тетраэдров и пирамид».
16.Найдите дополнение множества А до множества В, если А= {х 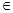R, х≥8} и
В= {х 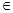R, х>4}.
A.В\А = (4; 8].
B.А\В = (4;+∞).
C.А\В = (4; 8) U (8; +∞).
D.В\А = [8; +∞).
17. Найдите декартово произведение множеств А и В, если А={а, б, в} и В={а, б}.
A.А ×В = {а; б; в}.
B.А ×В = {(а; б), (б; а), (в; а)}.
C.А ×В= {(а; а), (а; б), (а; в), (б; а)}.
D.А ×В= {(а; а), (а; б), (б; а), (б; б), (в; а), (в; б)}.
18. Декартово произведение каких множеств задано?
A. 
А= R; В= {3, 4}.
B.А= {3, 4}; В= R.
C.А= [3, 4]; В= [4, 3].
D.А= [3, 4]; В= R.
19.Множество N-«натуральных чисел» разбито на классы с помощью подмножеств А- «множество чисел, кратных 5» и В- «множество чисел, кратных 6». Какой класс, из предложенных в ответах, может быть в этом разбиении?
A.Множество чисел, кратных 5.
B.Множество чисел, кратных 6.
C.Множество натуральных чисел.
D.Множество натуральных чисел, некратных 5и 6.
20. Какой способ решения этой задачи верный: «Из пунктов А и В одновременно навстречу друг другу выехали велосипедист и мотоциклист. Скорость велосипедиста 10 км\ч, скорость мотоциклиста 30 км\ч. Через сколько часов движения они будут друг от друга на расстоянии 80км, если расстояние между пунктами А и В равно 200км?»?
A.(200-30): (80+10).
B.(200-80): (10+30).
C.(200-30): (80-10).
D.200: (10+30)-80.
Б) Тестовое задание.
1. Предельная абсолютная погрешность разности приближенных чисел равна:
А) разности предельных абсолютных погрешностей уменьшаемого и вычитаемого;
Б) разности предельных относительных погрешностей уменьшаемого и вычитаемого;
В) сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого;
Г) сумме предельных относительных погрешностей уменьшаемого и вычитаемого.
2. Предельная относительная погрешность частного приближенных чисел равна:
А) сумме предельных относительных погрешностей делимого и делителя;
Б) разности предельных относительных погрешностей делимого и делителя;
В) произведению предельных относительных погрешностей делимого и делителя;
Г) частному предельных относительных погрешностей делимого и делителя.
3. Предельная абсолютная погрешность числа 13,4 <x< 13,6 равна
А) 0,2;
Б) 0,1;
В) 0,05;
Г) 0,74.
4. Предельная относительная погрешность числа 9,18 ± 0,04 равна
А) 0,43;
Б) 0,44;
В) 0,04;
Г) 0,05.
5. На опытной делянке измерили рост пяти саженцев в сантиметрах: 122, 120, 156, 148, 124. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
А) 22;
Б) 10;
В) 12;
Г) 20.
6. Размах выборки 12,1; 12,4; 12,5; 12,4; 12,1; 12,4 равен
А) 0,2;
Б) 6;
В) 12,4;
Г) 0,4.
7. Ветеринар взвесил поросят. Их масса в килограммах такова: 82, 88, 96, 94, 95, 90, 88, 84, 99, 87. Мода и медиана этого набора чисел равны
А) 88 и 99;
Б) 88 и 95;
В) 88 и 88;
Г) 88 и 90.
8. Для службы на подводной лодке отбирают призывников ростом не более 165см. Есть 4 группы призывников, про которые известно следующее:
А) в первой группе средний рост равен 162см;
Б) во второй группе максимальный рост равен 169см;
В) в третьей группе минимальный рост равен 158см;
Г) в четвертой группе медиана ряда роста равна 163см.
В какой из групп половина призывников заведомо годна к службе на подводной лодке?
9. Ломаная линия, вершинами которой являются точки (хi; yi), определяемые элементами статистического ряда, называется
А) диаграммой частот;
Б) гистограммой частот;
В) медианой частот;
Г) полигоном частот.
10. Варианта выборки, делящая вариационный ряд на две части, равные по числу вариант, называется
А) модой;
Б) размахом;
В) медианой;
Г) средним арифметическим.
Критерии оценки усвоения знаний, сформированности умений:
| Задание | Показатели оценки результата |
| Задание А Задание Б | «Отлично» – 18-20 верных ответов. «Хорошо» – 15-17 верных ответа. «Удовлетворительно» – 12-14 верных ответов. «Неудовлетворительно» – менее 12 верных ответов. «Отлично» – 9-10 верных ответов. «Хорошо» – 7-8 верных ответа. «Удовлетворительно» – 5-6 верных ответов. «Неудовлетворительно» – менее 5 верных ответов. |
Комплект экзаменационных материалов
В состав комплекта входят:
1. Билеты с заданиями (количество заданий на 2 больше списочного состава студентов в группе).
2. Описание условий проведения экзамена
- На выполнение тестового задания А отводится 1 час 20 мин;
- На выполнение тестового задания Б отводится 40 мин;
- За каждое задание ставится отдельная отметка.
3. Оценочная ведомость.