Главная | Обратная связь

Графическое определение аномалии силы тяжести двухмерных тел с помощью палетки Гамбурцева.

1. Прямая задача. Для тел более сложной формы расчет 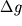представляет большие трудности и выполняется либо на вычислительных машинах, либо графическим путем с помощью различных палеток. Для вычислений аномалий над телами с сечением любой произвольной формы и вытянутыми вдоль оси (двухмерные тела) применяется палетка Гамбурцева. Палетка имеет вид, показанный на рис. 1.6.

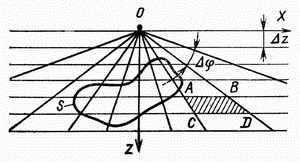
Рис.1.6 Палетка Гамбурцева для вычисления притяжения двухмерных тел

Здесь из точки О через один и тот же угол 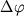проведены радиусы, а через равные расстояния - параллельные линии.

Сила тяжести 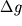в точке О за счет притяжения бесконечной горизонтальной призмой сечением в виде трапеции ABCD одинакова для любой из таких призм и равна

(1.15)

В самом деле, воспользуемся формулой притяжения бесконечно длинным цилиндром (1.12), в которую вместо \lambda подставим массу элементарной призмы сечением dxdz:

Притяжение бесконечно длинной призмой любого сечения может быть рассчитано по формуле:

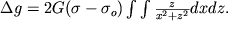
Заменив получим но 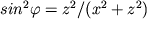, поэтому

где - цена одной трапеции (цена палетки), равная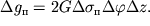

Подобрав 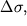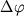и такими, чтобы равнялось какому-нибудь постоянному значению (например, 0,1 мГал), легко рассчитать в точке О аномалию от призмы любого сечения, для чего надо подсчитать число трапеций, покрывающих сечение исследуемого тела (n). Аномалия 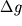равна n, умноженному на цену палетки и масштабный коэффициент

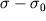где и - избыточная плотность и масштаб палетки, а и - избыточная плотность и масштаб разреза.

Таким образом, аномалия над двухмерным телом любого сечения с помощью палетки Гамбурцева рассчитывается по формуле:

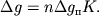
(1.16)

2. Обратная задача. Используя (1.16) с помощью палетки Гамбурцева, можно выяснить форму и положение сечения возмущающего двухмерного аномалосоздающего объекта. Для этого надо знать избыточную плотность 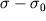, оценить аналитическим способом положение ее центра и для нескольких точек графика 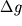построить возможные сечения возмущающего тела. Среднее из них характеризует примерное сечение тела.