Главная | Обратная связь

Исследование функций на экстремум.

Лекции Приложения производных

План

1. Исследование функций на возрастание и убывание.

2. Исследование функций на экстремум.

3. Исследование функций на выпуклость и вогнутость, нахождение точек перегиба.

4. Вертикальные, горизонтальные и наклонные асимптоты.

5. Общий план исследования функции и построения графика функции.

6. Теоремы о дифференцируемых функциях.

 

Исследование функций на возрастание и убывание.

Определение. Функция , определенная на числовом множестве , называется неубывающей (невозрастающей) на , если

Неубывающие и невозрастающие на множестве функции называются монотонными на этом множестве.

Если в предыдущем определении неравенства строгие, то соответствующие функции называются строго возрастающими (строго убывающими). Строго возрастающие (строго убывающие) функции называются строго монотонными функциями.

 

Признак монотонности. Для того, чтобы дифференцируемая на (a;b) функция не убывала (не возрастала) на этом интервале, необходимо и достаточно, ее производная была во всех его точках неотрицательна (неположительна).

Если производная функции во всех точках (a;b) положительная (отрицательная), функция строго возрастает (строго убывает). Последнее условие является достаточным, но не необходимым условием строгого возрастания. Пример: - строго возрастает на R, однако не всюду больше 0: .

 

Исследование функций на экстремум.

 

Определение. Пусть функция f задана на некотором множестве 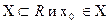. Точка называется точкой локального максимума (минимума) функции f, если существует такая окрестность U(x₀) точки , что "xÎU(x₀), x ≠ x₀, 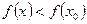(соответственно ).

Точки максимума (минимума) функции называются ее точками экстремума, значения функции в этих точках - ее экстремальными значениями (экстремумы функции).

Определение. Если функция определена в некоторой окрестности точки и в этой точке производная функции равна 0 или не существует, то точка называется критической точкой этой функции.

 

Необходимое условие экстремума (теорема Ферма). Если - точка экстремума функции , определенной в некоторой окрестности точки , то =0 или не существует.

Первый достаточный признак экстремума. Пусть функция (x) дифференцируема в некоторой окрестности точки , кроме, может быть, самой точки Î(a;b), в которой она является, однако, непрерывной. Если меняет знак с 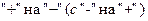при переходе через , то - точка максимума (минимума).