 |
|
Правило Лопиталя-Бернулли.
Теорема. Пусть функции f(x) и g(x) определены и дифференцируемы в некоторой проколотой d-окрестности 
точки a и, кроме того, 
f(x) = g(x) = 0 (или f(x) = g(x) = 
) и g¢(x) ¹ 0 "xÎ . Тогда, если существует 
, то существует и 
= .
Замечание. Если f¢(x) и g¢(x) удовлетворяют тем же требованиям, что и исходные функции f(x) и g(x), т.е. f¢(x) = g¢(x) = 0 ( f¢(x) = g¢(x) = ), f¢(x) и g¢(x) – дифференцируемы "xÎ , g¢¢(x) ¹ 0 "xÎ и существует 
, то правило Лопиталя-Бернулли можно применять повторно, т.е.
= = .
Раскрытие неопределенностей.
Неопределенности типа [0/0] и [∞/∞] раскрываются путем непосредственного применения правила Лопиталя-Бернулли.
Примеры.
1) 
= 
2) 
=- 
sin2px =0.
Неопределённости типа [¥ - ¥] и [0×¥] сводятся к неопределённостям и 
путём алгебраических преобразований.
[¥ - ¥]. f(x) = g(x) = ¥.
f(x) - g(x) = 
= .
[0×¥]. f(x) =0; g(x) = ¥.
f(x)×g(x) =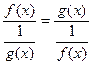 
.
Примеры.
1) 
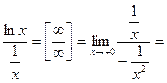xlnx = [0×¥] = 
- x = 0.
2) 
В случае неопределённостей вида [1¥], [00], [¥0] применяется методлогарифмирования.
Пусть y = f(x)g(x), f(x)>0. Тогда lny = g(x)lnf(x) Þ y= eg(x)lnf(x), где в показателе неопределённость типа [0×¥].
Примеры.
1) 
2) 
3) 
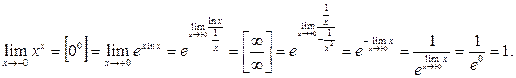
Формула Тейлора.
Определение. Пусть функция f(x) дифференцируема в точке x0 n раз. Многочлен
называется многочленомТейлора функции f(x) в точке x0; 
ОсновноесвойствомногочленаТейлора: 
Теорема Тейлора.
Если функция f(x) имеет в точке x0 и некоторой её δ – окрестности U(x0,δ) производные f´(x), f˝(x), …, f(n+1)(x), то "xÎU(x0,δ), x¹x0, существует точка xÎ( x0;x), что справедлива формула Тейлора f(x) = Pn(x)+Rn+1(x), где Pn(x) - многочлен Тейлора функции f(x) в точке x0, 
- остаточныйчленвформеЛагранжа.
Следствие. Пусть функция f(x) удовлетворяет условиям теоремы Тейлора. Тогда Rn+1(x)=o(x - x0)n при x ® x0 (остаточныйчленвформеПеано).
Замечание. Т.к. точка xÎ( x0;x), то x = x0 + Q(x - x0), где 0 < Q <1, тогда остаточный член в форме Лагранжа можно переписать в виде:
ФормулаТейлорадлямногочлена.
Если f(x) является многочленом степени n, т.е. f(x) = a0xn + a1xn-1 + ¼ + an-1x + an,
a0 ¹ 0, то f(n+1)(x) º 0. Из (*) Þ Rn+1(x) º 0 и для любых x, x0 Î R
Формула Маклорена.
ФормулойМаклорена называется формула Тейлора при x0 = 0.
Здесь остаточный член имеет вид:
1) в форме Лагранжа: 
2) в форме Пеано: Rn+1(x) = o(xn).
РазложениенекоторыхэлементарныхфункцийпоформулеМаклоренаприx®0.
Пример. Написать разложение функции esinx до x3.
Решение.
esinx = et, t = sinx.
т.к. sinx ~ x при x ® 0.