Главная | Обратная связь

Вивчення нового матеріалу.

Пошук у ширину.

 

Раніше ми вже розглядали різноманітні пошукові алгорит­ми: пошук заданої інформації в одновимірному масиві, в ме­режі, у рядку. Під час дослідження задач, що пов’язані з оброб­кою інформації, яку можна представити у вигляді графів, та­кож постає питання пошуку. У першу чергу - це пошук шляху від однієї заданої вершини до іншої.

Існує два підходи до здійснення такого пошуку. Розглянемо перший із них - пошук у ширину.

Вивчення нового матеріалу.

Як відомо, одним із найпоширеніших способів представлен­ня графа є матриця суміжності. Саме на перегляді цієї матриці і базується метод пошуку в ширину.

Для зручнішого пояснення цього методу розглянемо конкрет­ний приклад графа, зображеного на малюнку 21, а та відповідній йому матриці суміжності (мал. 21, б). Нехай також відомо, що необхідно визначити існування у даному графі шляху від вер­шини 1 до вершини 7.

Почнемо пошук шуканої вершини 7 із заданої вершини 1 і зафіксуємо для себе цю інформацію, будуючи дерево пошуку, в якому на першому кроці нашого пошукового алгоритму є лише одна вершина 1 (мал. 22, а) та послідовність вершин, які перегля­даються (мал. 22, б). Встановимо покажчики перегляду вершин у послідовності так: верхній вказуватиме на номер вершини, з якої ми дивимося, а нижній - на номер останньої «видимої» вершини. Відповідно на першому кроці такою вершиною є єдина вершина 1.

І ще одна інформація, яка може бути нам надалі корисною. Якщо забігти наперед і розглянути заданий граф (мал. 21, а), то можна помітити, що вершину з номером 1 знову побачимо, коли перейдемо до перегляду вершин 2, 3 та 4. Але повертатися у неї немає сенсу, оскільки при цьому ми «зациклимося» і бу­демо крутитися на одному і тому самому місці. Тому варто за­пам’ятовувати номери вершин, у яких ми вже побували, для

того, щоб виключити їх надалі з перегляду. Яким чином мож­на реалізувати такий захист? Можна запропонувати два спосо­би: перший - проглядати послідовність переглянутих вершин (мал. 22, б), другий - використати множину для їх фіксації (мал. 22, в). Який з них ефективніший? Якщо кількість вер­шин невелика, то раціональніше скористатися множиною, як­що ж вона більша за 256 - то переглядом послідовності. Але у цьому разі інформацію про заданий граф необхідно представля­ти у вигляді списку суміжних вершин.

Продовжимо пошук вершини 7. З малюнка 21, а видно, що з вершини 1 ми бачимо вершини 2, 3 і 4. Ту саму інформацію ми можемо отримати і з таблиці суміжності (мал. 21, б), пере­глянувши рядок, що відповідає номеру вершини, з якої ми дивимося, тобто перший рядок таблиці. Давайте зафіксуємо цю інформацію у дереві пошуку (мал. 23, а), у послідовності номерів вершин, які ми переглянули (1) і які ми бачимо (2, 3, 4) (мал. 23,в). Серед них поки що шуканої вершини 7 немає.

Для подальшого пошуку перейдемо до однієї з нових вершин, які ми побачили. Це вершини 2, 3 і 4. У нашій послідовності (мал. 23, б) першою записана вершина 2, тому й перейдемо до неї. Які вершини ми бачимо з вершини 2 (мал. 21, а)? Це верши­ни 1, 3, 5 і 6. Цю саму інформацію можна отримати з другого рядка таблиці суміжності (мал. 21,6). Однак лише вершини 5 і 6 є новими, а вершини 1 і 3 ми вже бачили на попередніх кроках нашого алгоритму. Доповнимо дерево пошуку (мал. 24, а), по­слідовність переглянутих і «видимих» вершин (мал. 24, б) та множину (мал. 24, в) новою інформацією.

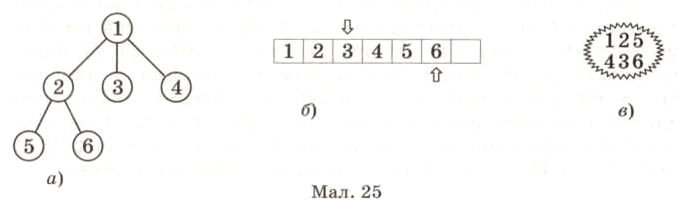
Чи завершили ми наш пошук? Зрозуміло, що ні, оскільки ні у дереві пошуку, ні у послідовності ми ще не дісталися шуканої вершини 7. Тому переходимо у послідовності вершин до на­ступної «побаченої» вершини 3. Тепер її можна буде назвати не лише «побаченою», але ще й «переглянутою». Згідно із зобра­женням графа і відповідної йому таблиці суміжності з вершини З ми бачимо вершини 1, 2, 4 і 5. Але вони не є новими, тому ми їх не фіксуємо ні у дереві пошуку, ні у послідовності вершин, ні у множині (мал. 25, а, б, в).

Переходимо до наступної вершини у послідовності, якою є вершина 4. Звідси ми бачимо вершини 1 і 3. Але і ці вершини вже є «побаченими», тому у нашому алгоритмі змінюється лише вершина, яку ми переглядаємо наступною. Такою верши­ною є вершина з номером 4, тобто наступна у нашій послідов­ності «переглянутих» і «видимих» вершин (мал. 26, б). З вер­шини 4 ми знову-таки нічого нового не побачимо, оскільки вершини 1 та 3 ми вже бачили раніше. Інформація на малюн­ках 26, а та 26, в залишилася незмінною.

Продовжуючи логіку нашого алгоритму, переходимо до вер­шини 5 - наступної у нашій послідовності (мал. 27, б). З верши­ни 5 ми бачимо вершини 2,3,7. Перші дві з цих вершин уже бу­ли переглянуті, а от вершина 7 не тільки нова, але й ще шука­на. Тому алгоритм можна вважати завершеним, а відповідь на поставлене на початку запитання буде такою: «У заданому графі вершина 7 є досяжною з вершини 1».

Проаналізуємо описаний алгоритм з точки зору його ре­алізації у вигляді програми. Як було вже сказано вище, інфор­мація про граф міститиметься у таблиці суміжності або у списку суміжності. Інформація про «переглянуті» і «побачені» верши­ни - в одновимірному масиві. Алгоритм обробки цього масиву відповідає роботі зі структурою даних «черга», де «голова» чер­ги вказує на поточну вершину, з якої ми дивимося далі, а «хвіст» вказує на останню видиму вершину. Під час виконання алгоритму «голова» переміщується вправо на нову вершину, в яку ми переходимо для подальшого перегляду нових вершин, а «хвіст» також переміщується вправо одночасно з дописуван­ням нових видимих вершин.

Тепер ми можемо проаналізувати умови завершення роботи алгоритму пошуку в ширину. Таких випадків є два: шукана вершина знайдена і відомий шлях до неї, або шукана вершина є недосяжною і шлях до неї відсутній.

Ми розглянули саме перший випадок пошуку вершини в графі, коли шукана вершина 7 є досяжною із заданої верши­ни 1. Шлях від вершини 1 до вершини 7 присутній у черзі, але без додаткової інформації він дещо прихований. Для отриман­ня цього шляху необхідно запам’ятовувати також і номери вер­шин, з яких ми побачили кожну наступну вершину. На малюн­ку 28 ця інформація позначена індексами для кожної поточної вершини, записаної у чергу.

Другий випадок може бути розтлумачений так: «голова» чгрги досягнула її «хвоста», асеред нових «побачених» вершин так і не з’явилася шукана. Це означає, що ми переглянули всі досяжні вершини графа, але не змогли дістатися до шуканої.

Підіб’ємо підсумок наших міркувань і опишемо алгоритм пошуку в ширину в словесній формі.

1. Вказати номер вершини k, з якої починається пошук за­даної шуканої вершини І.
2. Почати перегляд вершин заданого графа з вершини k, за­писавши її в чергу: і := k. Одночасно ця вершина є і останньою «побаченою» вершиною: j := k.
3. Зафіксувати всі нові вершини, які можна побачити з вер­шини і, в порядку зростання їх номерів, записуючи їх у чергу і збільшуючи при цьому на кожному кроці індекс «хвоста» чер­ги j на 1 (j := j + 1).
4. Якщо серед нових «побачених» вершин, записаних у чер­гу, є шукана вершина, то перейти до п. 8.
5. Для переходу до перегляду наступної «побаченої» верши­ни збільшити значення індексу «голови» черги і (і := і + 1).
6. Якщо значення індексу «голови» черги і збіжиться зі зна­ченням індексу його «хвоста» j, то перейти до п.10.
7. Перейти до перегляду наступної «побаченої» вершини і (п. 3).
8. Вивести інформацію про те, що шукану вершину І досяг­нуто і шлях до неї від вершини k існує.
9. Перейти до п. 11.
10. Вивести інформацію про те, що шукана вершина І недо­сяжна від вершини k і шлях до неї відсутній.
11. Завершити алгоритм.

Перейдемо до реалізації описаного алгоритму у вигляді фрагмента Pascal-програми:

head := 1; tail := 2; а[1] := k; {Ініціалізація початкових значень.}

flag := false; s := [k];

while (head < tail) and not flag do {«Голова» менша за «хвіст» та}

begin {не досягнуто шуканої вершини.}

і := 1; {Перегляд к-го рядка таблиці суміжності спочатку.}

while (І <= n) and not flag do {Вести пошук, доки не досягнуто кінця рядка}

begin {або не знайдено шуканої вершини.}

if (d[a[head], І]= 1) and not (І in S) {Якщо поточна вершина є «видимою»}

then {і ще не переглядалася, тоді}

Begin

a[tail] := І; S := S + [і]; {записуємо її у «хвіст» черги та додаємо}

inc(tail); {до множини, збільшуємо індекс «хвоста» черги.}

if і = I then flag := true; {Фіксуємо умову досягнення шуканої вершини.}

end;

inс(і) {Перехід до наступного елемента к-го рядка таблиці суміжності.}

end;

if not false {Якщо не досягнуто шуканої вершини,}

then inc(head) {то збільшуємо індекс «голови» черги.}

end;

If flag then write(f_OUt, ’YES’) {Інформація про те, що знайдено шукану вершину.}

{Інформація про те, що}

else write(f out, ’NO’); {не знайдено шукану вершину.}

Для реалізації алгоритму, що визначає шлях від заданої до шуканої вершини, необхідно зробити корективи.

Опис одновимірного масиву, який реалізує структуру даних «черги», можна запропонувати такий:

а: аггау[1 ..100] of record

top, prev: byte; end;

Початкові значення параметрів «черги» будуть такими: head := 1; tail := 2; a[l].top := k; a[i].prev := 0; а фрагмент програми, що поповнює «чергу» новими «видими­ми» вершинами, такий:

if (d[a[head].top, і] = 1) and not (і in s)

Then

Begin

a[tail].top := i; a[tail].prev := head;

inc(tail); s := s + [i];

if і = I then flag := true;

end;

Для виведення інформації про існуючий шлях від заданої вершини до шуканої можна запропонувати такий фрагмент програми мовою Pascal:

If flag then

Begin

writeln(f_out, ’YES’);

repeat {Виведення номера поточної вершини}

write(f_out, a[tail]-top, ’ ’); {визначеного шляху.}

{Перехід до вершини, з якої було видно}

tail := a[tail].prev; {поточну вершину шляху.}

until a[tail].prev = 0; {Завершення визначення шляху.}

write(f_OUt, a[tail].top); {Виведення номера вершини, що є початком шляху.}

End

else write(f_out, ’NO’);

Підіб’ємо остаточний підсумок розглянутого методу. По-пер­ше, тепер зрозуміло, чому цей метод носить назву «пошук у ши­рину». Адже дійсно ми ведемо пошук шуканої вершини, роз­глядаючи на кожному новому кроці одночасно всі нові вершини по рядках таблиці суміжностей, які ще не бачили. По-друге, можна зробити висновок, що метод пошуку в ширину дає най-

коротший шлях від заданої першими до шукішої. Для того щоб остаточно у цьому пересвідчитися, далі ми перейдемо до іншого методу - пошуку в глибину.

Спробуємо провести оцінку алгоритму пошуку в ширину. Під час формування черги з вершин заданого графа, що скла­дається з п вершин і т ребер, кожна вершина переглядається лише один раз. Це відповідає оцінці О(п). Але при цьому пере­глядаються всі ребра, яким належить поточна вершина. Отже, оцінка перегляду ребер становить 0(т). Оскільки перегляд ребер іде паралельно з переглядом вершин, що їм належать, то остаточна оцінка алгоритму визначається як 0(п + пі). Отже, можна зробити висновок, що час роботи алгоритму прямо пропорційний розміру заданого графа.