 |
|
Правила дифференцирования функций
Глава VII
Производная функции
Определение производной
Пусть дана функция 
, определенная в точке 
и ее окрестности. Изменим значение аргумента с до 
. Величина, показывающая, насколько изменился аргумент, называется приращением аргумента и обозначается 
. Таким образом, 
. При данном изменении аргумента значение функции изменится на величину 
, называемую приращением функции. Величины и 
не обязательно положительные.
Производной функции в точке называется предел отношения приращения этой функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Пример.
Пользуясь определением, найти производную функции 
.
Решение.
Числа 
и 
называются соответственно левой и правой производными функции в точке . Для существования производной функции в точке необходимо и достаточно, чтобы ее левая и правая производные в этой точке существовали и совпадали, т.е.
.
Функция, имеющая производную в точке , называется дифференцируемой в этой точке. Процесс нахождения производной называют дифференцированием.
Связь между дифференцируемостью и непрерывностью
Теорема.Если функция дифференцируема в некоторой точке, то она и непрерывна в этой точке.
Обратное утверждение неверно.
Пример. 
Покажем, что непрерывная функция 
(рис.15) не является дифференцируемой в точке 
.
Решение.
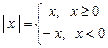. Найдем правую и левую производные:
.
Эти производные существуют, но не совпадают. Значит, в точке данная функция не имеет производной.
Функция является непрерывной, т.к.
.
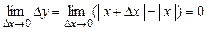Таблица производных
1. 
в частности, 
.
2. 
в частности, 
.
3. 
в частности,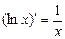 
.
4. 
.
5. 
.
6. 
.
7. 
.
8. 
.
9. 
.
10. 
.
11. 
.
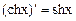12. 
.
13. 
.
Правила дифференцирования функций
I. Пусть С – постоянная и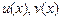 
– дифференцируемые функции. Тогда:
1. 
2. 
.
3. 
.
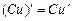4. 
.
5. 
.
II. Правило дифференцирования сложной функции:
Пусть функция имеет производную в точке , а функция 
имеет производную в точке 
. Тогда сложная функция 
в точке имеет производную, равную
.
Пример.
Найти производные следующих функций:
а) 
; б) 
; в) 
.
Решение.
а) Используя правило дифференцирования 4, получим
.
б) По правилу дифференцирования 5 имеем
.
в) По правилу дифференцирования сложной функции, полагая
, получим
.