 |
|
Геометрический смысл производной
Касательной к графику функции  в точке
в точке  называется предельное положение секущей ММ0, когда
называется предельное положение секущей ММ0, когда  по кривой
по кривой  .
.
Пусть  (рис.16). Из
(рис.16). Из  имеем
имеем  . Если
. Если  , то
, то  , где a – угол наклона касательной к графику функции
, где a – угол наклона касательной к графику функции  в точке
в точке  к оси Ох, т.е.
к оси Ох, т.е.
 .
.
Значение производной  равно угловому коэффициенту касательной к графику данной функции в точке
равно угловому коэффициенту касательной к графику данной функции в точке  .
.
Уравнение касательной к кривой  в точке
в точке  имеет вид:
имеет вид:
 .
.
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Уравнение нормали имеет вид:
 , при условии
, при условии  .
.
 |
|
Пусть даны две пересекающиеся в точке  кривые
кривые  и
и  , причем обе функции имеют производные в этой точке. Тогда углом между этими кривыми называется угол между касательными к ним, проведенными в точке
, причем обе функции имеют производные в этой точке. Тогда углом между этими кривыми называется угол между касательными к ним, проведенными в точке  :
:
 .
.
Пример.
Написать уравнения касательной и нормали к кривой  в точке
в точке  .
.
Решение.
Так как  , то
, то  , а
, а  . Получаем уравнение касательной:
. Получаем уравнение касательной:
 или
или 
и уравнение нормали:
 или
или  .
.
Пример.
Найти угол, под которым пересекаются кривая  и прямая
и прямая  .
.
Решение.
Найдем точку пересечения графиков этих функций. Для этого решим уравнение  . Теперь найдем уравнение касательной к графику функций
. Теперь найдем уравнение касательной к графику функций  в точке
в точке  . Т.к.
. Т.к. 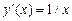 , то
, то  ;
; 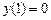 . Значит, уравнение касательной имеет вид
. Значит, уравнение касательной имеет вид  .
.
Угол, под которым пересекаются в точке  прямая
прямая  и касательная
и касательная  и является искомым углом. Так как
и является искомым углом. Так как  и
и  , то
, то  .
.
Задачи.
Пользуясь только определением производной, найти  :
:
7.1.  ; 7.2.
; 7.2.  ;
;
7.3.  ; 7.4.
; 7.4.  ;
;
7.5.  ; 7.6.
; 7.6.  ;
;
7.7.  ; 7.8.
; 7.8.  .
.
Найти производные следующих функций:
7.9.  ; 7.10.
; 7.10.  ;
;
7.11.  ; 7.12.
; 7.12.  ;
;
7.13.  ; 7.14.
; 7.14.  ;
;
7.15.  ; 7.16.
; 7.16.  ;
;
7.17.  ; 7.18.
; 7.18.  ;
;
7.19.  ; 7.20.
; 7.20.  ;
;
7.21.  ; 7.22.
; 7.22.  ;
;
7.23.  ; 7.24.
; 7.24.  ;
;
7.25.  ;7.26.
;7.26. 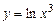 ;
;
7.27. 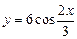 ; 7.28.
; 7.28.  ;
;
7.29.  ; 7.30.
; 7.30.  ;
;
7.31.  ; 7.32.
; 7.32. 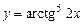 ;
;
7.33.  ; 7.34.
; 7.34.  ;
;
7.35.  ; 7.36.
; 7.36.  ;
;
7.37.  ; 7.38.
; 7.38.  ;
;
7.39.  ; 7.40.
; 7.40.  .
.
7.41. Найти производные гиперболических функций:
а)  ; б)
; б)  ;
;
в) 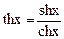 ; г)
; г)  .
.
Написать уравнения касательной и нормали к графику функции  в данной точке и сделать рисунок:
в данной точке и сделать рисунок:
7.42.  ; 7.43.
; 7.43.  ;
;
7.44.  ; 7.45.
; 7.45.  ;
;
7.46.  ; 7.47.
; 7.47.  .
.
Найти углы, под которыми пересекаются заданные кривые:
7.48.  ;
;
7.49.  ;
;
7.50.  ;
;
7.51.  .
.
5. Дифференциал функции
Пусть функция  дифференцируема на интервале
дифференцируема на интервале  . Производная этой функции в некоторой точке
. Производная этой функции в некоторой точке 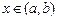 определяется равенством
определяется равенством  , поэтому можно записать
, поэтому можно записать
 ,
,
где  при
при  . Умножая все члены последнего равенства на
. Умножая все члены последнего равенства на  , получаем
, получаем  . Приращение состоит из двух слагаемых, первое из которых при
. Приращение состоит из двух слагаемых, первое из которых при  есть главная часть приращения, линейная относительно
есть главная часть приращения, линейная относительно  . Произведение
. Произведение  называется дифференциалом функции и обозначается через
называется дифференциалом функции и обозначается через  :
:
 .
.
Т.к.  , т.е. дифференциал независимой переменной равен приращению этой переменной, то
, т.е. дифференциал независимой переменной равен приращению этой переменной, то
 .
.
Основное использование дифференциала функции – приближенные вычисления, т.к. при  справедливо приближенное равенство:
справедливо приближенное равенство:

или
 .
.
Пример.
Вычислить приближенно:  .
.
Решение.
Пусть  ,
,  . Тогда
. Тогда  ,
,  ,
,  .
.
Используя свойство первого дифференциала, получаем
 .
.
Задачи.
7.52. Найти приращение 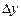 и дифференциал
и дифференциал  в общем виде, а также в точке
в общем виде, а также в точке  , если известно
, если известно  :
:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
Вычислить приближенно с помощью свойства дифференциала:
7.53.  ; 7.54.
; 7.54.  ;
;
7.55.  ; 7.56.
; 7.56.  ;
;
7.57.  ; 7.58.
; 7.58. 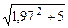 ;
;
7.59.  ; 7.60.
; 7.60.  .
.
6. Производные и дифференциалы высших порядков
Пусть функция  дифференцируема на некотором интервале
дифференцируема на некотором интервале  . Значения производной
. Значения производной  зависят от
зависят от  , т.е. производная
, т.е. производная  также представляет собой функцию от
также представляет собой функцию от  . Дифференцируя эту функцию, можно получить вторую производную
. Дифференцируя эту функцию, можно получить вторую производную  от функции
от функции  , т.е.
, т.е. 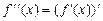 . Производной n-го порядка от функции
. Производной n-го порядка от функции  называется производная первого порядка от производной
называется производная первого порядка от производной  -го порядка и обозначается символом
-го порядка и обозначается символом  или
или  :
:  . Аналогично вводятся дифференциалы высших порядков. Дифференциал от первого дифференциала функции называется дифференциалом второго порядка и обозначается:
. Аналогично вводятся дифференциалы высших порядков. Дифференциал от первого дифференциала функции называется дифференциалом второго порядка и обозначается:  .
.
Найдем выражение для второго дифференциала. В силу общего определения дифференциала имеем:  , т.к.
, т.к.  не зависит от
не зависит от  . Дифференциалом n-го порядка называется первый дифференциал от дифференциала
. Дифференциалом n-го порядка называется первый дифференциал от дифференциала  -го порядка:
-го порядка:  .
.
Пример.
Найти производную и дифференциал второго порядка функции
 .
.
Решение.
Используя правило дифференцирования сложной функции, находим
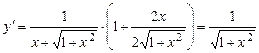 ,
,  .
.
Следовательно,
 ,
,  .
.
Задачи.
Найти производные и дифференциалы 2-го порядка от следующих функций:
7.61.  ;
;
7.62.  ;
;
7.63. 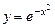 ;
;
7.64.  .
.
7.65. Найти  , если
, если 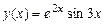 .
.
7.66. Найти  , если
, если  .
.
Правило Лопиталя
Теорема Лопиталя.(Раскрытие неопределенности типа  ).
).
Пусть функции  и
и  определены и дифференцируемы в некоторой окрестности
определены и дифференцируемы в некоторой окрестности  точки
точки  , кроме, быть может, самой этой точки, и
, кроме, быть может, самой этой точки, и  . Тогда, если
. Тогда, если  и существует
и существует  , то существует и
, то существует и 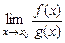 , причем
, причем
 .
.
Замечание 1. Правило Лопиталя можно применять повторно.
Замечание 2. Теорема верна в случае 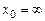 .
.
Замечание 3. Теорема верна в случае, если
 ,
,
(т.е. имеет место неопределенность типа  )
)
С помощью тождественных преобразований к основному типу  или
или  можно свести неопределенности других типов, таких, как
можно свести неопределенности других типов, таких, как
 .
.
Пример.
Вычислить пределы по правилу Лопиталя:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
Решение.
а) при  получаем неопределенность типа
получаем неопределенность типа  :
:
 ;
;
б) при  получаем неопределенность типа
получаем неопределенность типа  . Чтобы раскрыть ее, применяем правило Лопиталя дважды:
. Чтобы раскрыть ее, применяем правило Лопиталя дважды:
 ;
;
в) здесь имеем неопределенность типа  :
:
 ;
;
г) здесь имеем неопределенность типа  :
:

д) здесь имеем неопределенность типа  . Обозначим
. Обозначим  и прологарифмируем это равенство по основанию е:
и прологарифмируем это равенство по основанию е:
 .
.
В правой части этого равенства при  имеем неопределенность типа
имеем неопределенность типа  . Применяя дважды правило Лопиталя, находим
. Применяя дважды правило Лопиталя, находим

Следовательно, 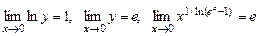 .
.
Задачи.
Вычислить пределы по правилу Лопиталя:
7.67.  ; 7.68.
; 7.68.  ;
;
7.69.  ; 7.70.
; 7.70.  ;
;
7.71.  ; 7.72.
; 7.72.  ;
;
7.73.  ; 7.74.
; 7.74. 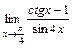 ;
;
7.75.  ; 7.76.
; 7.76.  ;
;
7.77.  ; 7.78.
; 7.78.  ;
;
7.79.  ; 7.80.
; 7.80.  ;
;
7.81.  ; 7.82.
; 7.82.  ;
;
7.83.  ; 7.84.
; 7.84.  ;
;
7.85.  ; 7.86.
; 7.86.  ;
;
7.87.  ; 7.88.
; 7.88.  ;
;
7.89.  ; 7.90.
; 7.90.  ;
;
7.91.  ; 7.92.
; 7.92.  .
.
8. Формула Тейлора
Если функция имеет производные до  -го порядка включительно в некоторой окрестности точки
-го порядка включительно в некоторой окрестности точки  , то для всякого
, то для всякого  из этой окрестности справедлива формула Тейлора (порядка n):
из этой окрестности справедлива формула Тейлора (порядка n):

где  - остаточный член формулы Тейлора. Остаточный член позволяет оценить ошибку в результате замены функции ее многочленом Тейлора
- остаточный член формулы Тейлора. Остаточный член позволяет оценить ошибку в результате замены функции ее многочленом Тейлора

т.е.  .
.
Имеются различные формы записи остаточного члена  . Наиболее удобна для анализа и запоминания форма Лагранжа:
. Наиболее удобна для анализа и запоминания форма Лагранжа:
 .
.
На практике часто рассматривают случай, когда 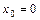 , тогда
, тогда
 –
–
формула Маклорена.
Смысл формулы Тейлора, как и формулы Маклорена, состоит в том, что функция сложной «природы» заменяется многочленом. Если в формуле Тейлора (Маклорена) отбросить остаточный член, то получится приближенная формула, заменяющая данную функцию многочленом n-й степени.
Приближенные формулы основных элементарных функций:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
В частном случае, когда  – целое число, получаем бином Ньютона:
– целое число, получаем бином Ньютона:
 .
.
Данные формулы эффективно используются при вычислении пределов функций.
Пример.
Вычислить предел:  .
.
Решение.
Заменяя  и
и 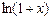 их разложениями по формуле Маклорена
их разложениями по формуле Маклорена  ,
,  , получаем
, получаем
 .
.
Задачи.
7.93. Многочлен  разложить по степеням
разложить по степеням  .
.
7.94. Многочлен  разложить по степеням
разложить по степеням  .
.
7.95. Многочлен  разложить по степеням
разложить по степеням  .
.
7.96. Многочлен  разложить по степеням
разложить по степеням  .
.
7.97. Разложить по формуле Тейлора функцию  до 4-го порядка включительно в точке
до 4-го порядка включительно в точке  .
.
7.98. Разложить по формуле Тейлора функцию  до 4-го порядка включительно в точке
до 4-го порядка включительно в точке  .
.
Используя формулы Маклорена основных элементарных функций, написать первые n членов формулы Маклорена (без остаточного члена) для следующих функций:
7.99.  ; 7.100.
; 7.100.  ;
;
7.101.  ; 7.102.
; 7.102.  .
.
Вычислить пределы, используя известные разложения в ряд Маклорена:
7.103.  ; 7.104.
; 7.104.  ;
;
7.105.  ; 7.106.
; 7.106.  ;
;
7.107.  ; 7.108.
; 7.108.  ;
;
7.109.  ; 7.110.
; 7.110.  .
.