 |
|
Шифрування й розшифрування
RSA
Матеріал з Вікіпедії — вільної енциклопедії.
RSA — криптографічна система з відкритим ключем.
RSA став першим алгоритмом такого типу, придатним і для шифрування і для цифрового підпису. Алгоритм використовується у великій кількості криптографічних застосунків.
Зміст
- 1 Історія
- 2 Опис алгоритму
- 2.1 Генерування ключів
- 2.2 Шифрування й розшифрування
- 2.3 Цифровий підпис
- 3 Деякі особливості алгоритму
- 3.1 Генерація простих чисел
- 3.2 Доповнення повідомлень
- 3.3 Вибір значення відкритого показника
- 3.4 Вибір значення секретного показника
- 4 Довжина ключа
- 5 Застосування RSA
- 6 Примітки
- 7 Література
Історія
Опис RSA було опубліковано у 1977 році Рональдом Райвестом, Аді Шаміром і Леонардом Адлеманом з Масачусетського Технологічного Інституту (MIT).
Британський математик Кліфорд Кокс (Clifford Cocks), що працював в центрі урядового зв'язку (GCHQ) Великобританії, описав аналогічну систему в 1973 році у внутрішніх документах центру, але ця робота не була розкрита до 1997 року, тож Райвест, Шамір і Адлеман розробили RSA незалежно від роботи Кокса.
В 1983 році був виданий патент 4405829 США, термін дії якого минув 21 вересня 2000 року.
Опис алгоритму
Безпека алгоритму RSA побудована на принципі складності факторизації. Алгоритм використовує два ключі — відкритий (public) і секретний (private), разом відкритий і відповідний йому секретний ключі утворюють пари ключів (keypair). Відкритий ключ не потрібно зберігати в таємниці, він використовується для шифрування даних. Якщо повідомлення було зашифровано відкритим ключем, то розшифрувати його можна тільки відповідним секретним ключем.
Генерування ключів
Для того, щоб згенерувати пари ключів виконуються такі дії:
1. вибираються два великі прості числа 
і 
приблизно 512 біт завдовжки кожне
2. обчислюється їх добуток 
3. обчислюється функція Ейлера 
4. вибирається ціле 
таке, що 
та взаємно просте з 
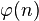
5. за допомогою розширеного алгоритму Евкліда знаходиться число 
таке, що 
Число 
називається модулем, а числа і — відкритою й секретною експонентами (англ. encryption and decryption exponents), відповідно. Пари чисел 
є відкритою частиною ключа, а 
— секретною. Числа і після генерації пари ключів можуть бути знищені, але в жодному разі не повинні бути розкриті.
Шифрування й розшифрування
Для того, щоб зашифрувати повідомлення 
обчислюється
.
Число 
і використовується в якості шифртексту. Для розшифрування потрібно обчислити
.
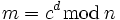Неважко переконатися, що при розшифруванні ми відновимо вихідне повідомлення:
З умови
випливає, що
для деякого цілого 
, отже
Згідно з теоремою Ейлера:
,
тому
RSA припущення — RSA є односторонньою переставкою, тобто для будь-якого дієвого алгоритму A:
нехтовно мала, що означає неможливість обернення RSA без секретної інформації — .
Наведений вище варіант шифрування називається підручник RSA (англ. textbook RSA) і є цілком уразливим[1]. В жодному разі його не можна використовувати в криптосистемах.
Цифровий підпис
RSA може використовуватися не тільки для шифрування, але й для цифрового підпису. Підпис 
повідомлення 
обчислюється з використанням секретного ключа за формулою:
Для перевірки правильності підпису потрібно переконатися, що виконується рівність
